이 블로그글은 2019년 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 딥러닝 홀로서기 세미나를 수강하고 작성한 글임을 밝힙니다.

Convolutional Neural Network (CNN)

MLP의 문제점

Number of parameters

• 이전 layer 들의 모든 뉴런들이 다음 layer에 연결되기 때문에 모델이 깊어질수록 파라미터가 기하급수적으로 증가한다.
• 실제로 몇몇의 의미없는 파라미터가 존재하게 된다.

→ 결국엔, 모델 capacity가 증가하고, 학습 시간이 증가하며 overfitting 문제가 발생한다.

Loss of spatial structure in input data

• MLP의 경우 입력데이터를 1차원 벡터로 처리해야 한다.

→ , 입력 데이터의 공간적 정보가 손실 되어버린다.

• 공간적 정보 : 이미지 내 픽셀들이 만들어내는 형태, 패턴, 상대적 위치

💡 (해결책) CNN을 도입해보자.

Convolutation Neural Netowrk (CNN)

사람은 어떻게 인식을 할까?

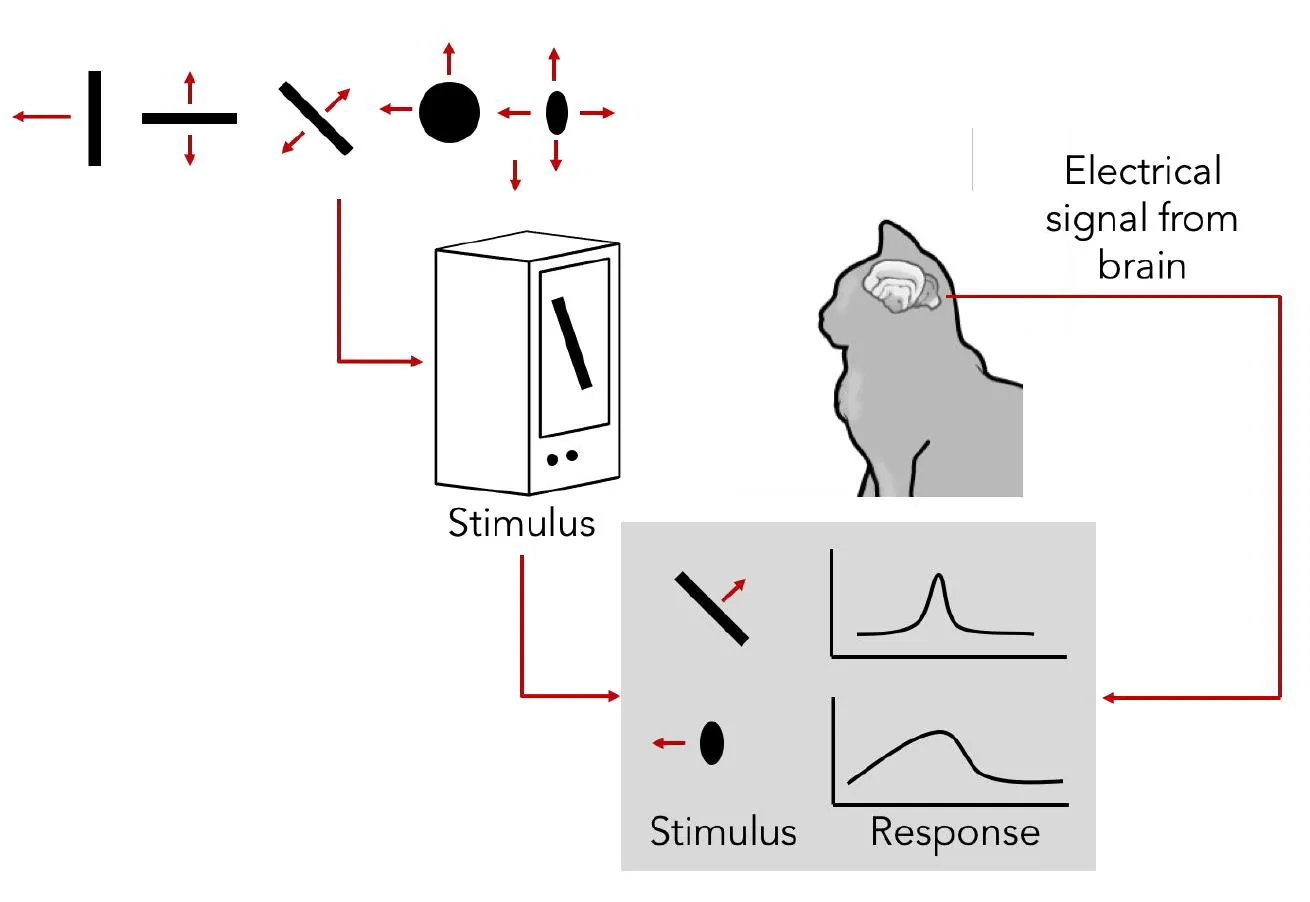
• 사람이 인식을 어떻게 하는지에 대한 해답을 찾기 위해, 과학자들은 고양이를 대상으로 전극을 이용한 뇌 실험을 수행했다.
• 이 실험을 통해 '서로 다른 간단한 정보를 담당하는 뉴런이 존재할 것이다'라는 가설이 실제로 입증되었다.

Hierachical organization

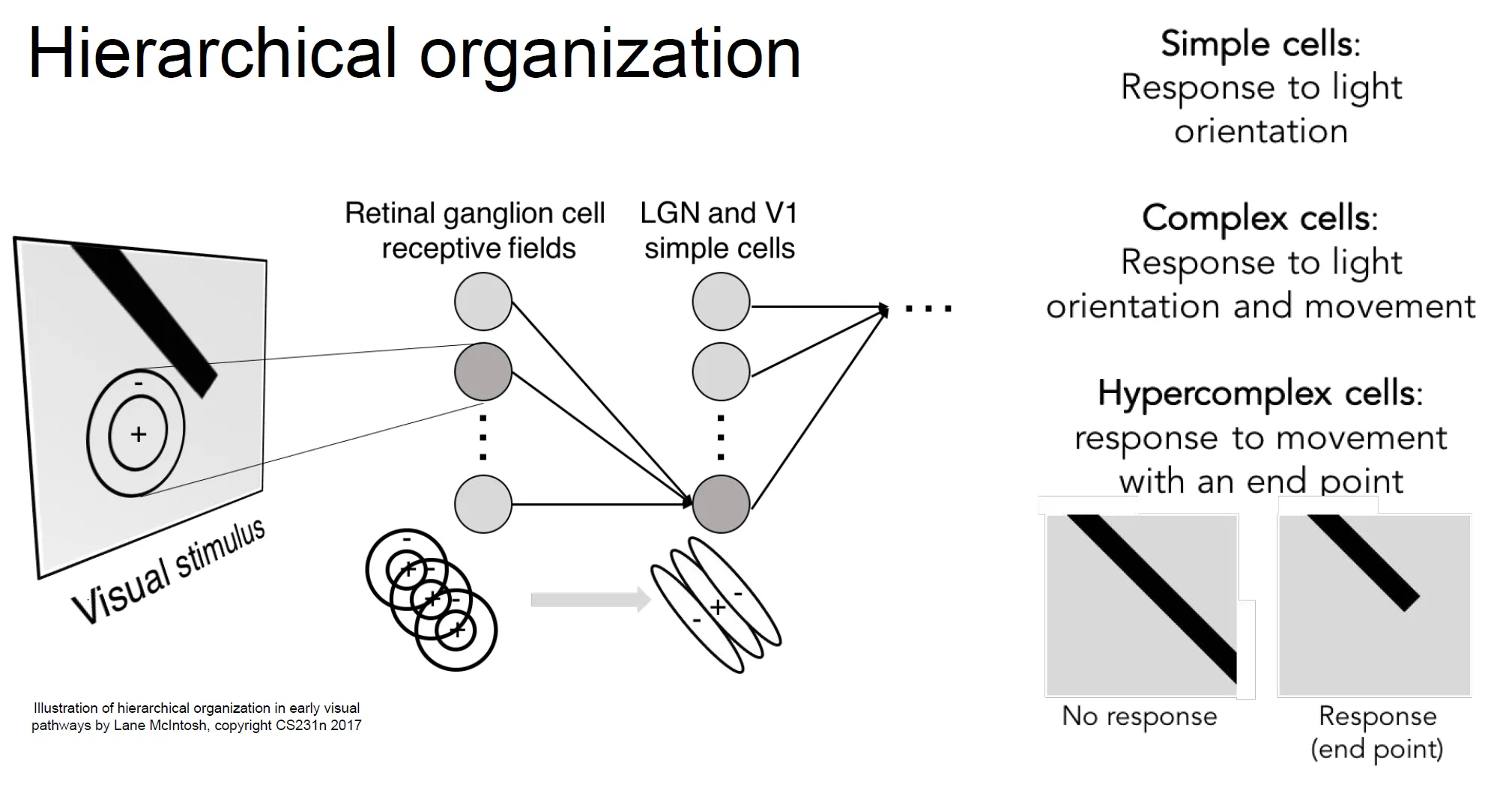
• 결국, 뉴런들은 계층적인 구조를 가지고 있음을 알게 되었다.
  • 얕은 계층은 단순한 정보(예: 빛의 방향, 경계선 등)에 반응하는 뉴런들이 존재한다.
  • 깊은 계층으로 갈수록 이러한 단순한 정보를 결합하여 더 복잡하고 고차원적인 정보(예: 움직임, 형태 등)를 처리하는 뉴런들이 활성화된다.

MLP / Fully Connected Layer

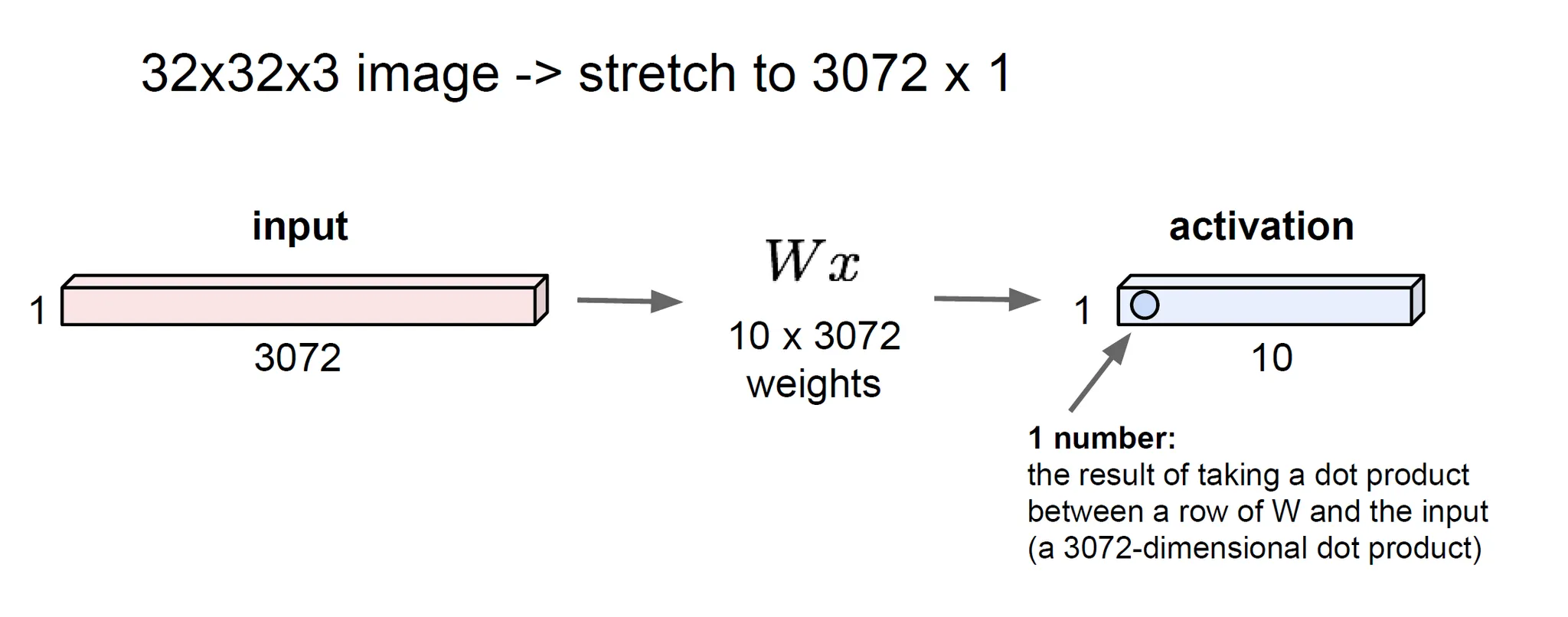
• 정리하면, MLP는 하나의 뉴런이 모든 이전의 뉴런들을 연결하는 구조
• 1차원 벡터를 입력으로 받기 때문에 이미지의 경우 공간적 구조를 잃어버림

Convolution Layer

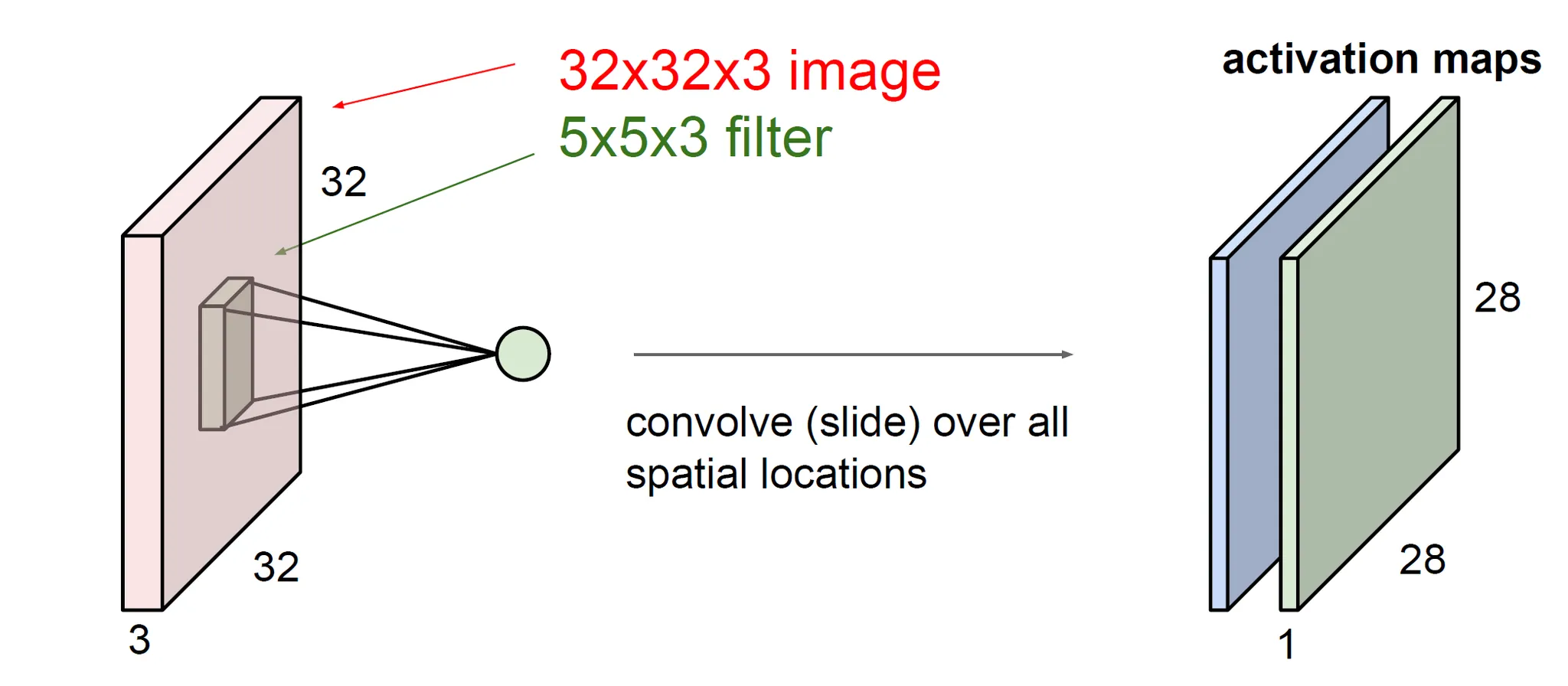
• Filter map을 입력에 오버랩 시킨 후 dot product로 계산 (합성곱 연산):
  • Filter map을 입력 데이터 위에서 슬라이딩하며, 해당 영역과 dot product(요소별 곱셈 후 합산)를 계산한다.
  • 이 결과값들을 조합하여 Activation map을 생성한다.
• 공간적 구조를 보존함:
  • 입력 데이터의 위치적 정보를 유지하면서 특징을 추출한다.
  • 이를 위해 패딩(Padding)과 스트라이드(Stride)를 적절히 조정하여 입력과 출력 간의 구조적 관계를 조율한다.

💡 Filter map, Activation map이란?

• Filter map: 입력 데이터의 특징을 탐지하기 위해 학습된 가중치로 이루어진 작은 크기의 행렬을 말한다.
• Activation map: Filter map이 탐지한 특징의 출력 결과로, 입력 데이터의 특정 영역에서 특정 패턴(엣지, 텍스처 등)이 얼마나 활성화되었는지 나타낸다.

Convolutional Network

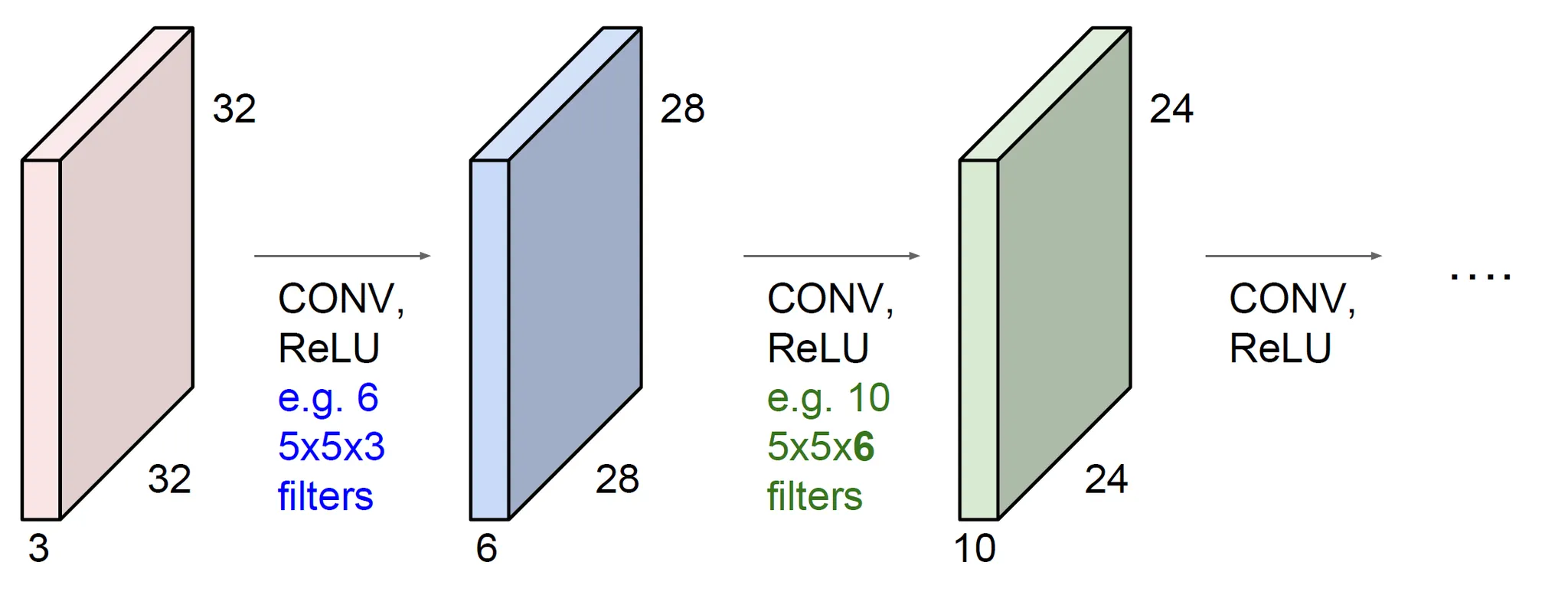
• Convolutional Layer를 쌓은 구조

• 이전 Convolutional Layer의 출력인 Activation map이 다음 Layer의 입력으로 작용한다.

• 이때 어떻게 Activation map의 크기가 결정될까?

  • 출력의 가로, 세로 사이즈 : 필터 사이즈와 패딩(Padding)과 스트라이드(Stride)에 의해 결정
  • 채널 수 : 필터의 개수와 같음

패딩(Padding)

• 입력 데이터 가장자리에 0을 추가하여 입력 크기를 늘리는 과정
• 목적
  • 보통 이미지의 크기를 유지하기 위해 사용함
    • 깊이가 깊어짐에 따라 이미지 크기가 작아지면 더 깊은 깊이로 쌓을 수 없기 때문이다
  • 가장자리 정보 손실 방지

스트라이드(Stride)

• 필터가 입력 위를 이동하는 간격
• 목적
  • 출력 크기를 조절하기 위해 사용한다.

뉴런 관점에서 Convoultion Layer의 해석

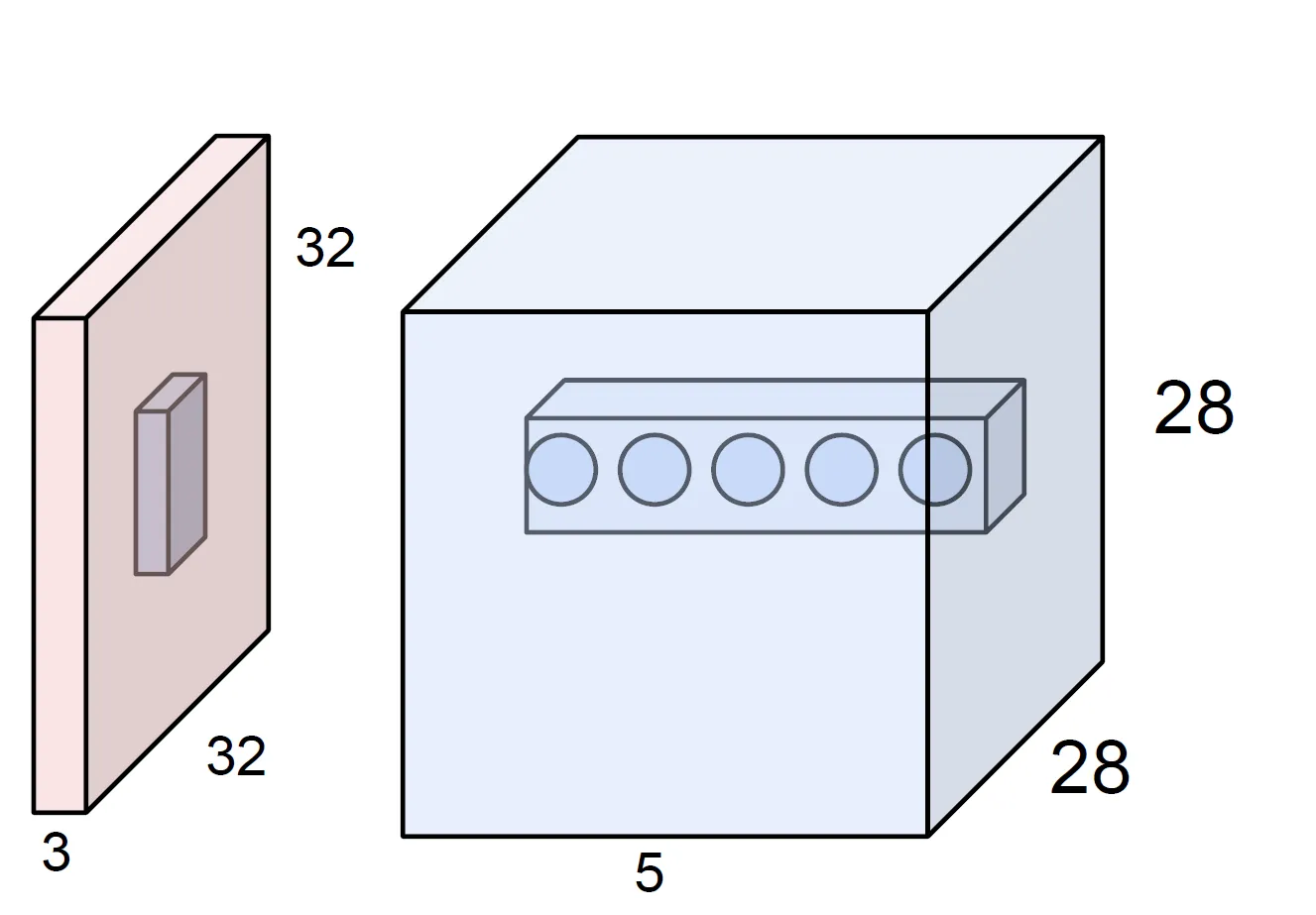
Local Connectivity

• 정의 : CNN에서 각 뉴런이 입력의 일부 작은 영역(receptive field)에만 연결된다.
• 특징
  • 필터의 크기 = 뉴런이 볼 수 있는 이미지의 크기 (recpetive field)
    • 첫 번째 layer에서는 필터 크기에 해당하는 작은 Receptive Field로 단순한 정보를 학습한
    • layer가 깊어지면 깊이질수록 더 큰 receptive field를 가지게 되고 고차원(복잡한) 정보를 담당

weighted sharing

• 정의 : CNN에서 동일한 필터가 입력 데이터의 모든 위치에서 동일한 가중치를 사용한다.
• 특징
  • 하나의 필터로 이미지 전체를 스캔하며 동일한 특징을 감지한다.
  • 가중치 공유를 통해 학습 파라미터 수가 크게 감소한다.
  • 이미지의 위치에 관계없이 동일한 특징을 감지할 수 있다.

Convolutional network의 전체 구조

• CONV (Convolution)
  • 이미지의 작은 영역(Receptive Field)에 필터를 적용하여 특징 맵을 생성
• RELU (Rectified Linear Unit)
  • 비선형 활성화 함수로, 음수 값을 0으로 변환해 비선형성을 추가
• POOL (Pooling)
  • 특징 맵의 크기를 축소(예: Max Pooling)하여 연산량을 줄이고 과적합 방지
• FC (Fully Connected)
  • 모든 뉴런이 연결된 레이어로, 입력된 특징을 기반으로 클래스 예측을 수행
  • 최종 분류 단계

Pooling layer

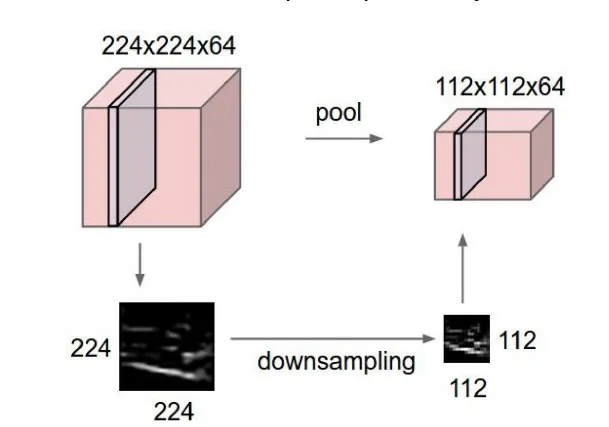
• 이미지는 각 픽셀이 가지는 정보가 제한적일 수 있기 때문에, Pooling Layer는 이미지에서 발생할 수 있는 불필요한 세부 정보를 줄이고 중요한 특징만 남긴다.
• 이미지 크기가 결국 down sampling되는 효과
• 특징
  • 이미지의 해상도를 줄이며, 출력 데이터의 크기를 감소시킨다.
  • 크기를 줄임으로써 후속 레이어에서 처리해야 할 데이터 양이 줄어들어 계산량이 줄어든다.
  • 중요한 특징을 유지하면서, 이미지의 위치나 크기 변화에 덜 민감하게 만든다. (이미지의 정확한 위치보다는 전체적인 패턴과 특징에 집중)
  • 이미지에서 중요하지 않은 픽셀 정보를 줄이고, 중요한 정보만 강조한다.

Max pooling

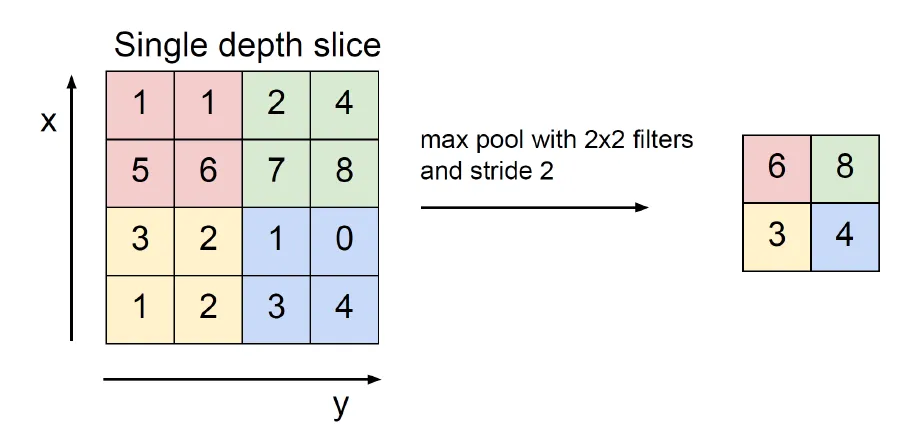
• Max Pooling이 2x2 필터와 스트라이드(stride) 2를 사용해 입력 데이터를 축소하는 과정을 말한다.
• 최대 풀링의 경우 필터내의 가장 큰 값만 유지한다.

Fully Connected Layer

• 질문 : 왜 마지막 단에서 Fully Connected Layer를 사용하는가?
• 해답

  • CNN의 앞 단에서 이미지의 고차원적이고 중요한 정보를 담은 Feature Vector를 추출한다.

  • FC Layer는 이 Feature Vector의 모든 값을 보고(전체적인 패턴을 분석한 결과) 최종적으로 Classification(분류)이나 Regression(회귀)을 수행한다.

    즉, Fully Connected Layer는 예측을 위해 CNN이 학습한 정보를 통합하여 최종 결정을 내리는 역할을 한다.