Text classification

Naive Bayes

• 딥러닝을 적용하기 이전에 가장 간단한 부류 방식

• Baye's Theorem: 데이터 D가 주어졌을 때 , 각 클래스 c의 확률

• $P(D|c) \times P(c)$ 를 통해 Class 'Y' 예측

$P(Y = c |x =w_1,w_2,...w_n)$
$\doteq P(x= w_1,w_2,...w_n |Y=c)P(Y=x)$
$\approx P(w_1|c)P(w_2|c) ... P(w_n|c)P(c)$
$=\prod_{i=1}^{n}P(w_i|c)P(c)$

• 사후 확률 $P(c|D)$을 최대화 하는 c를 찾는다

$\hat{c}= argmax_{c\in C}P(Y = c |x =w_1,w_2,...w_n)$
$= argmax_{c \in C}\prod_{i=1}^{n}P(w_i|c)P(c)$

• 사전 확률 $P(c)/ 특징 별 가능도 확률 P(D|c)$: 실제 데이터에서 출현한 빈도로 추정

$P(Y=c) \approx \frac{Count(c)}{\sum_{i=1}^{|C|}Count(c_i)}$
$P(w|c) \approx \frac{Count(w,c)}{\sum_{j=1}^{|V|}Count(w_j,c)}$

문제점 : 출현 횟수로만 확률을 추정하면 불확실성 발생

smoothing으로 각 출현 횟수에 1을 더함(0 방지)

• Naive Bayes 한계점: 단순히 출현 빈도를 세어 확률으 구해서 쉽고 간단한 감성 분석이 가능하지만 긱 단어의 Feature는 서로 독립적이다 라는 가설은 한계가 존재한다. 언어에서는 순서로 인한 관계와 정보 중요

Rnn 활용

• 마지막 은닉 상태로 텍스트의 클래스 분류

• 입력의 원-핫 벡터를 위치 인덱스로 기억, Embedding layer 통과
• 초기 hidden state와 단어 Embedding Tensor를 Rnn에 통과
• 모든 time-step에 대한 출력과 마지막 hidden state 반환
• 마지막 time-step으로 softmax를 통과하여 이산확률 분포 표현 -> $\hat{y}$
• $\hat{y} \ \&\ y$ 차이를 구하는 Cross Entropy Loss 최소화

Cnn 활용

• 자연어 처리에서는 주변 단어에 따라 서로 영향을 받기 때문에 Rnn에 국한되어있지만, 합성곱 연산을 이용한 CNN으로고 구현 가능
  

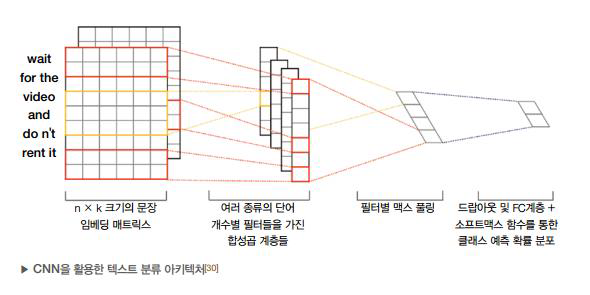
• CNN은 주어진 이미지에 kernel이 차례로 합성곱 연산 수행

• 연산 후에는 입력보다 차원이 감소(padding을 통해 입출력 차원 유지 가능)

• 원-핫 벡터의 인덱스를 표현하는 단어 임베딩은 1차원 벡터

• 문장 내의 모든 time-step의 단어 임베딩 벡터를 합치면 2차원 행렬

• 그 후 CNN 합성곱 연산 수행

• CNN 계층의 결과 값: filter 별 점수(각 Feature 별 score)

• 결과 값을 max pooling하여 각 문장의 feature에 대한 최고 점수 추출

• 가변 길이의 CNN 결과 값을 고정 길이로 변환 -> 문장의 임베딩벡터

• softmax를 통과하여 이산확률 분포 표현

이진 분류

• 2개의 클래스를 갖는 이진 분류에서는 sigmoid함수 사용
• 손실 함수는 Binary Cross Entropy loss 함수 사용
• 기존의 Cross entropy loss에 이진 분류 특화 $BCELOSS(\hat{y},y) = - (y \times log \hat{y} +(1-y) \times log (1-\hat{y})$

멀티 이진 분류

• 신경망의 마지막 계층에 n개의 노드를 주고 sigmoid 함수 적용
• 최종 loss 함수는 다음과 같음
  

멀티 레이블 분류

• 여러 개의 클래스가 동시에 정답이 될 수 있는 것 (ex: 감정 분석(긍정,중립, 부정))
• 레이블 n개의 softmax 계층 필요, Cross Entropy 손실 함수 사용