우리는 손실함수를 최소화하기 위해 경사하강법을 사용하고, 경사하강법을 통해 가중치를 업데이트하기 위해서는 손실함수의 미분계수가 필요함. 이때 우리가 일반적으로 사용하는 수치 미분을 사용하여 미분계수를 구할 경우, 각 변수를 모두 미분해야 하므로 계산량이 많아지고 이는 너무나 비효율적인 방법임.

따라서 연쇄 법칙(Chain Rule)를 기반으로 한 역전파(Backpropagation)를 사용하게 됨.

Backpropagation in DNN

아래와 같은 DNN의 상황에서 Backpropagation을 계산해보겠음.
초록색 노드는 bias를 더해주는 node임.

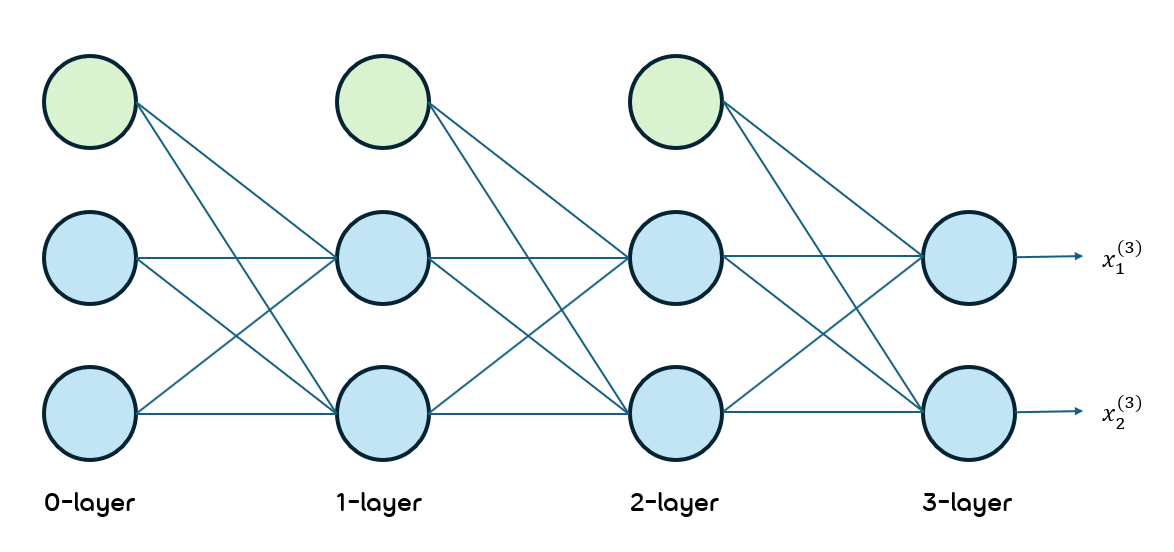
우선 사용할 기호들에 대해 아래와 같이 정의하겠음.

$x_n^{l+1}=g(s_n^l)$
$g(x) : activation function$
$s_n^l$ : l번째 layer에서 l+1번째 layer의 n번째 node로 보내는 값
$W_{ab}^l$ : l번째 layer의 a번째 node에서 l+1번째 layer의 b번째 node로 보낼 때의 가중치

따라서
$x_1^{(3)}=g(s_1^{(2)})$이고, $s_1^{(2)}=W_{01}^{(2)}+W_{11}^{(2)}x_1^{(2)}+W_{21}^{(2)}x_2^{(2)}$가 성립함. 이와 동일하게
$x_2^{(3)}=g(s_2^{(2)})$와 $s_2^{(2)}=W_{02}^{(2)}+W_{12}^{(2)}x_1^{(2)}+W_{22}^{(2)}x_2^{(2)}$ 또한 성립함.
우리는 이 식을 바탕으로 Chain Rule을 적용해 미분해 나갈거임.

손실함수를 $f$ 라고 설정하면, 우리는 각 가중치들을 업데이트하기 위해 각 가중치에 대하여 $f$를 미분한 값을 찾아내야 함.

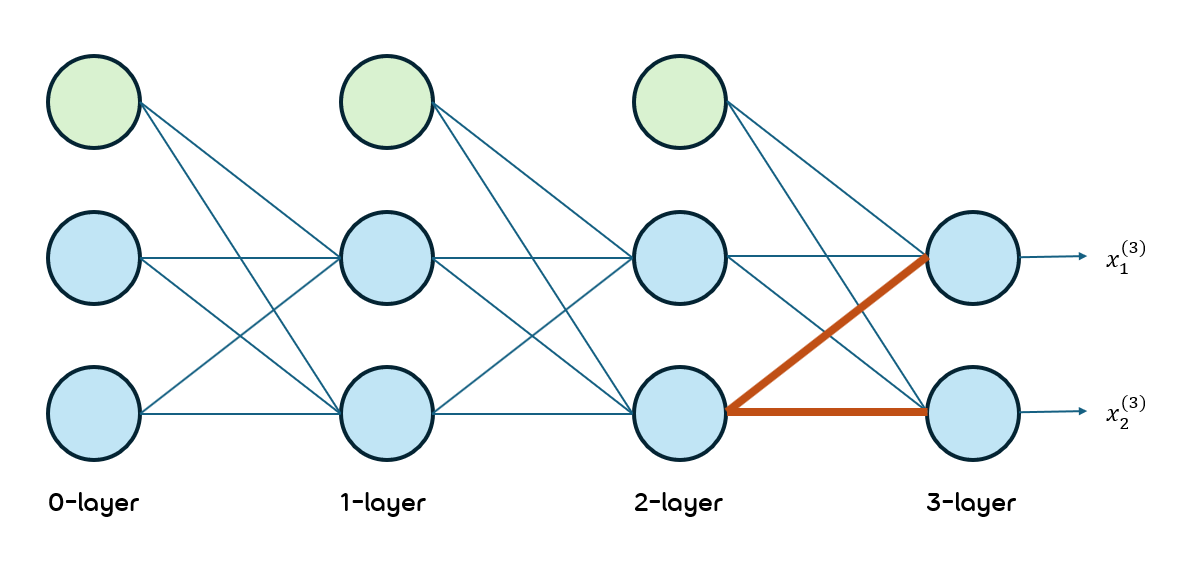
우선 아래 경로에 대한 미분값을 찾아보겠음.
빨간 경로에 해당하는 가중치 행렬은 $W_{21}^{(2)}$와 $W_{22}^{(2)}$임.

Chain Rule을 적용하여 나타낸 결과는 아래와 같음.

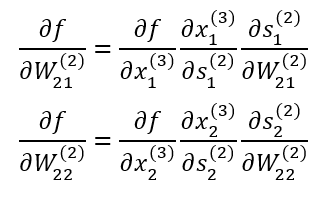
이때 $s$를 $W$에 대해 미분한 값에 대해서는 위의 식을 바탕으로 계산하여 나타낼 수 있음.
또한 그 앞의 두 미분값을 아래와 같이 치환하겠음.

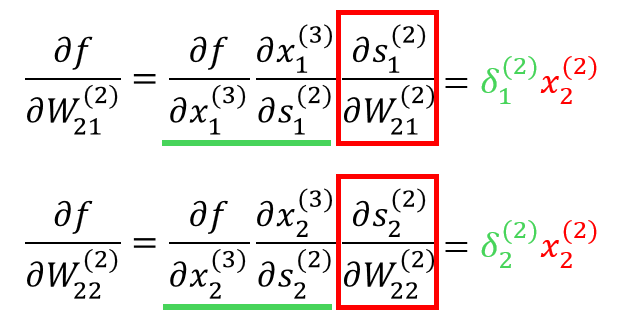
다음으로는 아래 빨간색 경로의 가중치에 대한 미분값을 계산해보겠음. 그런데 이번에는 해당 가중치가 뒤의 두 초록색 경로에 영향을 주고 있으므로 이를 고려하여 계산할 필요가 있음.


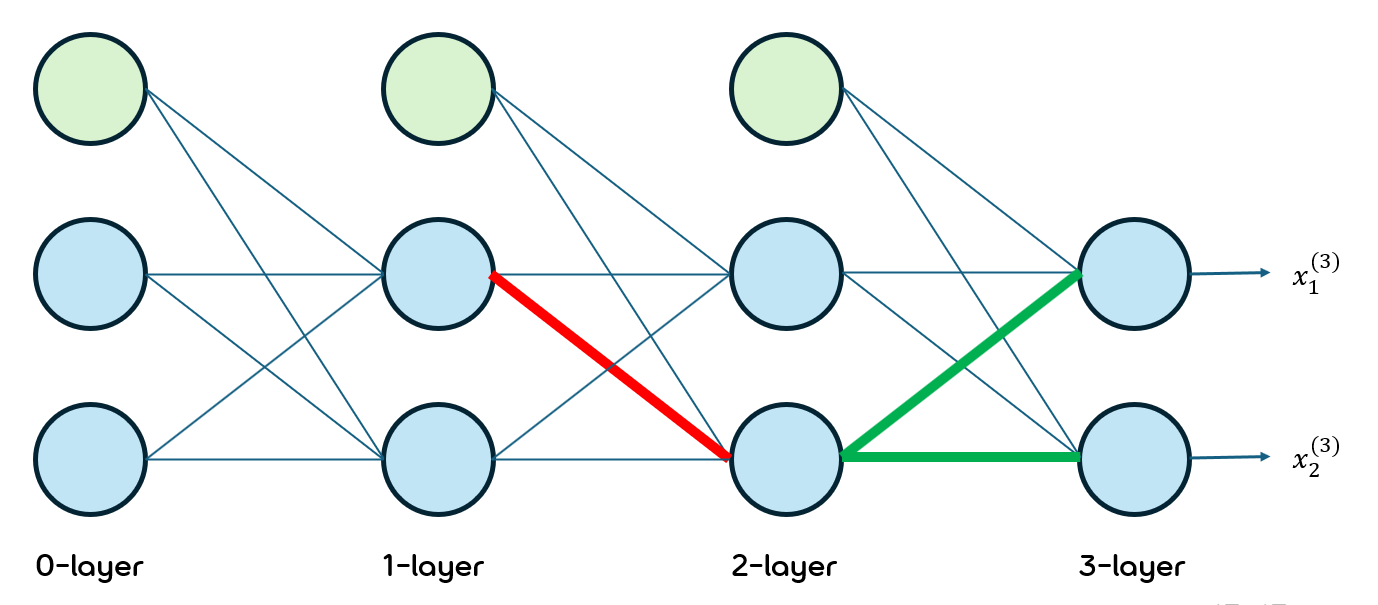
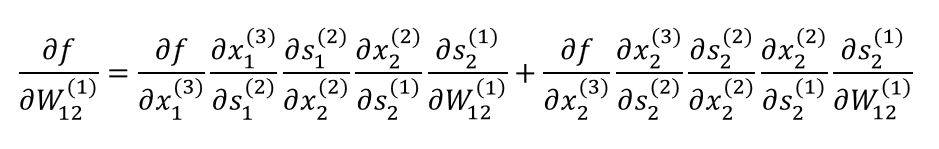
해당 가중치의 값이 마지막 두 노드의 값에 영향을 미치므로 마지막 두 노드를 나누어 미분한 후 더하였음.
위 수식을 자세히 관찰해보면 처음에 델타로 치환하였던 값과 같은 부분도 있고, 직접 미분값을 계산할 수 있는 부분도 있음. 이를 적용하여 식을 풀어내면 아래와 같이 계산됨.

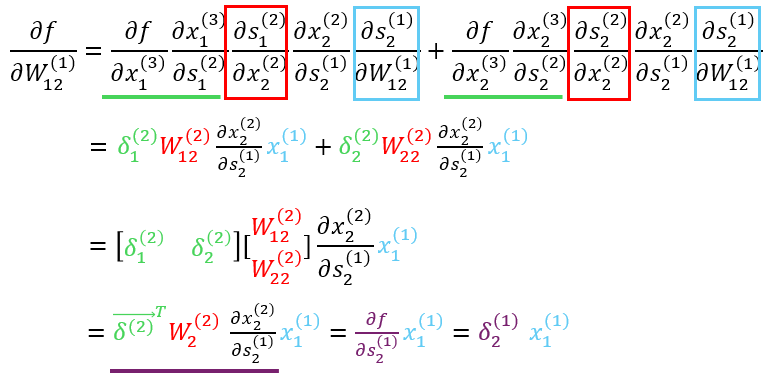
수식의 최종 결과를 보면 처음 계산했던 두 가중치 미분 결과와 꼴이 매우 비슷하다는 것을 볼 수 있음. 그리고 델타는 다음 layer의 델타값을 참조하는 것을 보아 oupput layer에서부터 input layer 방향으로 미분해 나가면 복잡하게 미분할 필요없이 이전에 사용한 미분값을 사용하여 쉽게 계산할 수 있을 것이라는 것도 알 수 있음.

일반화하여 전체 layer의 개수 $L$에 대하여 $l\leq L-2$의 범위를 가질 때 아래와 같은 식이 성립함.

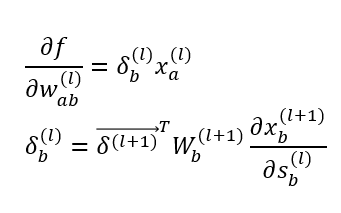
정리하면 인공신경망의 학습 과정은 다음과 같음.

1. 순전파 과정을 통해 출력
2. 출력값을 바탕으로 오차함수 계산
3. 오차함수의 각 가중치에 대한 미분계수를 역전파로 계산
4. 얻어낸 미분계수로 경사하강법 적용 후 가중치 업데이트
5. 1~4 과정 반복

Vanishing Gradient

역전파 계산에 등장하는 문제점 중 하나임. 특히 이 기울기 소실(Vanishing Gradient)은 활성화함수로써 Sigmoid를 사용할 때 많이 발생함.

Sigmoid는 아래와 같이 생겼음.

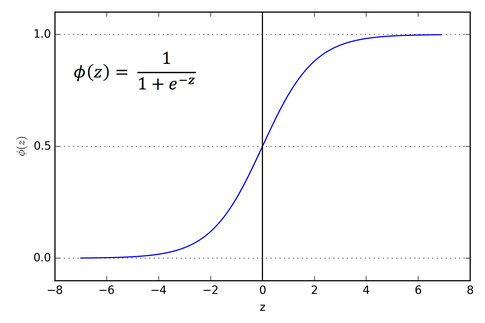
이 함수는 $x=0$일 때 기울기가 $1/4$으로, 함수 내에서 가장 큰 기울기임. 그리고 $x$가 무한대로 갈수록 그 기울기는 빠르게 0에 가까워짐.

이러한 함수의 특징 때문에 역전파 계산에서 활성화함수를 미분한 값을 사용할 때 layer가 쌓일수록 미분값이 점점 0에 가까워지는 것임. 즉 아무리 layer를 많이 쌓아도 output layer에 가까운 layer의 가중치만 조금 업데이트되고, input layer에 가까운 layer의 가중치는 거의 업데이트가 안된다는 것임.

따라서 이는 sigmoid에만 해당하는 문제가 아닌 기울기가 점점 0으로 소실되는 함수들 모두에 해당하는 문제가 됨.

그렇다면 어떤 함수를 써야 하는가?
대표적인 함수가 바로 ReLU임.

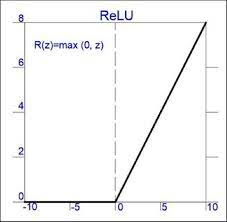
sigmoid와 달리 값이 양수라면 기울기가 항상 1이기 때문에 활성화함수의 미분값으로 인해 기울기가 소실될 문제를 완전히 해결했음. 또한 값이 음수인 값에 대해서는 기울기가 모두 0이기 때문에 모든 노드에 대한 미분값을 반영하는 것이 아닌 일부 노드만 반영한다는 특징도 있음. 이 또한 기울기 소실 문제를 줄이는 데에 영향을 줌.

그렇다면 ReLU를 사용하는 것이 항상 기울기 소실 문제에 대해 옳은가?
그건 또 아님.

ReLU는 값이 하나라도 음수가 나온다면 그 노드에 대한 미분값을 0으로 처리해버리는 상남자 함수이므로, 노드의 개수가 충분하지 않은, 노드의 개수가 매우 적은 신경망에 대해서는 오히려 가중치 업데이트를 정상적으로 하지 못할 가능성이 더 높음. 따라서 노드의 개수가 충분히 많지 않다면 기존의 sigmoid 함수를 사용하는 것이 기울기 소실이 발생하더라도 더 학습을 잘 할 수 있음.