[기초 통계학] 확률변수

융·2023년 4월 28일

기초통계학

[기초 통계학]

목록 보기

3/6

확률(Probability)

모든 경우의 수에 대한 특정 사건이 발생하는 비율이다.
확률 실험을 통해 얻은 모든 실험 결과 *표본 공간)들 중에 특정 사건(event)이 일어나는 것에 대한 확신의 정도

확률의 고전적 정의

어떤 사건의 발생 확률운 그것이 일어날 수 있는 경우의 수 대 가능한 모든 경우의 수의 비이다.

표본 공간(Sample Space)

어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합

동전 던지기 {앞면, 뒷면}
주사위 던지기 = {1,2,3,4,5,6}
사건 A가 일어날 확률을 P(A)라고 하고, 표본공간 (S) 가 유한 집합일때 표본 공간의 모든 원소들이 일어날 확률이 같으면

✒️ 예제

동전 두개를 던져서 뒷면이 한번만 나오는 확률은 얼마인가?

표본 공간 : {(앞, 뒤), (뒤, 앞), (뒤, 뒤), (앞, 앞)}
사건 A : {(앞, 뒤), (뒤, 앞)}
P(A) = 1/2

📌통계적 확률 (statistical probality)

과거의 경험이나 실제로 실험을 한 뒤에 나온 결과들을 바탕으로 계산한 확률

동전 두개를 던져서 뒷면이 한번만 나오는 확률 P(A) 는 수학적 확률에서 1/2 이다. 이는 앞면과 뒷면의 발생가능성이 동일하다고 가정하는 고전적 확률 이다.

실제 실험을 하면 확률이 다르게 나올 가능성이 크지만 동전 던지기는 무한히 반복한다면 상대도수의 극한(통계적 확률) 또한 1/2과 유사하게 수렴한다.

실험을 무한히 반복하면 n(A) / n 은 어떤 값으로 수렴하는데 이 극한 값을 사건 A가 일어날 확률로 해석하는 것을 통계적 확률이라 한다.

실험을 계속 반복한다는 것은 표본이 무수히 많아진다는 뜻이며 결국 모집단이 된다는것을 의미한다. 즉, 확률은 표본이 아니라 모집단이 어떤 형태로 이루어져 있는지 표시한것이며 상대도수의 극한은 많은 표본을 통해 모집단의 특성을 파악 한다고 해서 통계적 확률 이라고 한다.

참고 : 통계적 확률 | AI 꿈나무

확률의 성질

합사건(union) : 사건 A 또는 사건B가 일어날 확률 A∪B

곱사건(intersection) : 사건 A와 사건B가 동시에 일어날 확률 A∩B

배반사건(mutually exclusive event) : 사건 A와 사건B가 동시에
일어날 수 없을 경우 A∩B = ∮

여사건(complement) : 사건A가 일어나지 않을 확률 Ac

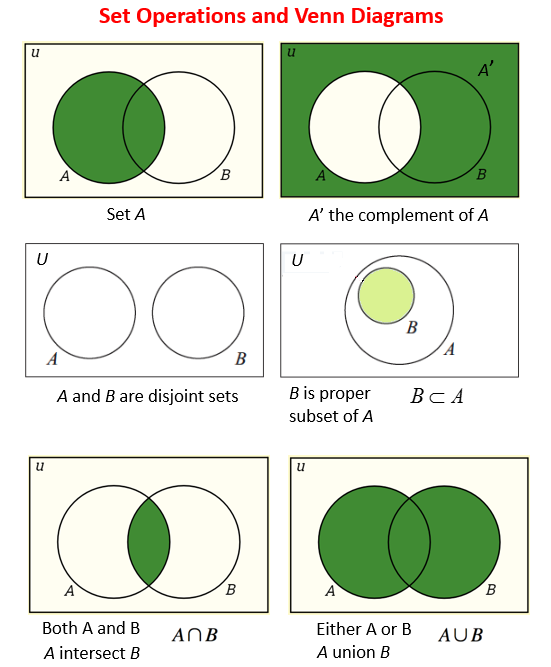
이미지 출처 : Set Operations - Union, Intersection, Complement

1) 확률의 덧셈법칙: : P(A∪B) = P(A) + P(B) − (A∩B)
2) A와 B가 배반 사건이면, P(A∩B) = P(∮) = 0
3) A의 여사건이 Ac 이면, P(A) + P(Ac) = 1

✒️ 예제

1부터 13까지 13장의 카드에서 한장을 뽑는 실험에서 아래의 사건을 생각해보자
A: 짝수를 뽑을 확률
B: 5이하의 카드를 뽑을 확률

(a) 표본공간을 정의하고 각 사건의 확률을 구하라

표본공간 : {1,2,3,4,5,6,7,8,9,10,11,12,13} , P(1) = p(2) = p(3) ... = P(13) = 1/13

(b) A와 B의 곱사건과 합사건을 구하라

A = {2,4,6,8,10,12} : P(A) = 6/13
B = {1,2,3,4,5} : P(B) = 5/13
A∩B = {2,4} : P(A∩B) = 2/13
P(A∪B) = P(A)+P(B)-P(A∩B) = (6+5-2)/13 = 9/13

조합과 순열

! (Factorial): n개를 일렬로 늘여 놓은 경우의 수를 n!로 표현하며,
n! = n(n-1)(n-2) … 2 * 1

순열(Permutation): 순서를 고려하여 n개 중 r개를 뽑아서 배열하는 경우의 수

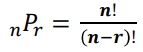
조합(Combination) : 순서를 고려하지 않고 n개중 r개를 뽑아서 배열하는 경우의 수

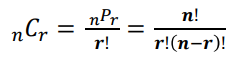
조건부 확률 (conditional probality)

주어진 사건이 일어났다는 가정 하에 다른 한 사건 일어날 확률 , 어떤 사건 A가 발생한 상황에서 또 하나의 사건 B가 발생할 확률 P(B|A)

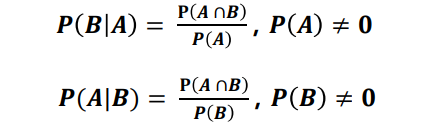
예제 - 주사위 굴리기
주사위를 굴린 후 숫자 1 이 나올 확률은 보통 1/6로 가정한다. 하지만 주사위를 굴리고 난 후, 얻은 숫자가 홀수라는 추가 정보가 있을때, 새로운 정보는 1 이 나올 확률을 계산할 때 영향을 미친다.

초기 표본 공간 {1,2,3,4,5,6} 에서 {1,3,5} 로 줄었기 때문이다.

위의 식을 정리하면
A : 주사위를 굴렸을때 1이 나오는 사건 -> P(A) = 1/6
B : 주사위를 굴렸을때 홀수가 나오는 사건 -> P(B) = 1/2
P(A∩B) = 숫자 1이 나올 확률 = 1/6

P(A|B) = 숫자가 홀수가 나온 후 그 수가 1일 확률 = P(A∩B) / P(B) = 1/3

확률의 곱셈 법칙

📌 베이즈의 정리

사후 확률을 사전 확률을 이용하여 표현하는 방법
조건부 확률울 이용하여 또 다른 조건부 확률을 계산하는 방법을 설명하는 정리

사후 확률이란 원인들의 영향을 비교하는 것
사건B or 사건C 가 원인이 되어 일어나는 사건A 가 있다. 사건A 가 100번 일어났을 경우 원인을 조사 한 결과 사건B 가 원인인 경우의 수는 40번, 사건C 가 원인인 경우의 수는 60번이다.

사건 A가 일어났을 때 원인이 B인 경우 = 40/100
사건 A가 일어났을 때 원인이 C인 경우 = 60/100

두 사건 모두 '사건A가 일어났던 것을 전제하고 있다' 이 두 확률이 바로 P(B|A), P(C|A) 이다.

따라서 사후 확률 P(B|A)는 사건 A가 일어났을 때, 다른 여러가지 원인들과 비교하여 사건 B가 얼마나 사건A가 발생하는데 영향을 주었는지 평가하는 것

P(B|A) 에서 사건 B가 사건 A가 일어나는데 얼만큼 영향을 주었는지는 계산하는 것이 베이즈 정리의 핵심으로, 베이즈 정리의 우변이 표현하고 있는 내용이다.

✒️예제

(1) 상자에서 공 뽑기

서로 다른 2개의 상자 A와 B가 있다.
상자 A에는 파란색 공 1개와 빨간색 공2개, 상자 B에는 파란색 공 2개와 빨간색 공 1개가 들어있다.
상자 A와 B중 한 상자를 뽑아 공 1개를 뽑는 시행을 생각하자. 꺼낸 색 공이 빨간색 일 때, 그 공이 상자 A에서 나왔을 확률은 얼마인가? (단, 2상자 중, 1상자를 선택할 확률은 0.5로 모두 같다고 가정한다.)

구하려는 것 P(A|Red) 
P(A) = 0.5
P(B) = 0.5
P(RED) = 3/6 = 1/2 = 0.5
P(RED|A) = 2/3 
P(A|Red) = P(RED|A)*P(A)/P(RED) =  (2/3*0.5)/0.5 = 2/3 = 0.0606

(2) 자동차 보험을 든 고객이 사고 날 확률
자동차 보험의 고객의 분포 A등급 30%, B등급 50%, C등급 20%이고, 각 고객 등급별로 1년내 사고의 확률은 A등급 0.1 B등급 0.2 C등급 0.3이라면

a) 임의의 한 고객을 선택했을때, 그 고객이 1년 이내에 사고를 낼 확률을 구하시오

b) 어떤 고객이 1년내 사고를 낸 고객이라면, 그 고객이 A등급일 확률을 구하시오


P(A) = 0.3
P(B) = 0.5
P(C) = 0.2
P(K|A) = 0.1
P(K|B) = 0.2
P(K|C) = 0.3 

(a) 
P(K) = 고객이 1년내 사고날 확률 
= P(A)*P(K|A) + P(B)*P(K|B) + P(C)*P(K|C) 
= (0.3*0.1) + (0.5*0.2) + (0.2*0.3) 
= 0.19 

(b)
P(A|K) 
= P(K|A) * P(A) / P(K)
= 0.1 * 0.3 / 0.19
= 0.15789

참고 : 베이즈 정리와 조건부 확률의 관계

확률 변수 (random variable)

표본공간 내에 있는 각 원소(s)에 하나의 실수값(R)을 대응 시키는 함수

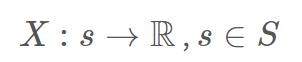
확률 현상에 기인해 결과값이 확률적으로 정해지는 변수를 의미한다.

일반적으로 확률 변수는 대문자로 표현하며, 확률변수의 특정값을 소문자로 표현함

이산확률변수(discrete random variable): 확률변수 X가 셀 수 있는 값들로 구성되거나 일정 범위로 나타나는 경우 (예 : 동전 던지기)
연속 확률 변수(continuous random variable): 확률변수 X가 연속형 또는 무한대와 같이 셀 수 없는 경우

예) 하나의 부품을 불량이나 양품으로 판정한다고 했을 때 확률변수 X = X : 1 부품이 불량 X : 0 부품이 정상으로 정의 가능

참고 : 확률변수(Random variable)

이산확률변수

확률변수 X가 갖는 값을 셀 수 있을 때 (나열 가능할 때), 그 확률변수 X를 이산확률변수라고 한다.

이산확률분포

확률변수 X의 값들을 나열했을 때 각각에 대한 확률의 대응 관계를 이산확률변수 X에 대한 확률분포라고 한다.

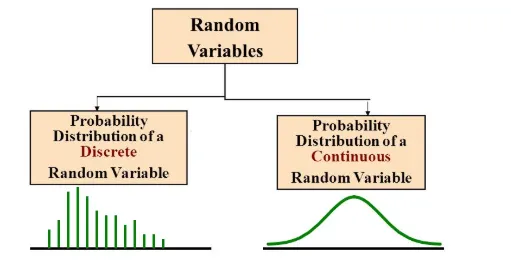
이미지 출처 : Probability Distributions: Discrete and Continuous

예제 - 동전 던지기

동전을 두번 던졌을 때 앞면(H), 뒷면(T) 의 조합이 나올 경우 : {HH, HT, TH, TT}
확률 변수 X 를 앞면이 나온 동전의 개수라고 정의
표본공간 : {HH, HT, TH, TT} => 실수 : {2,1,1,0}

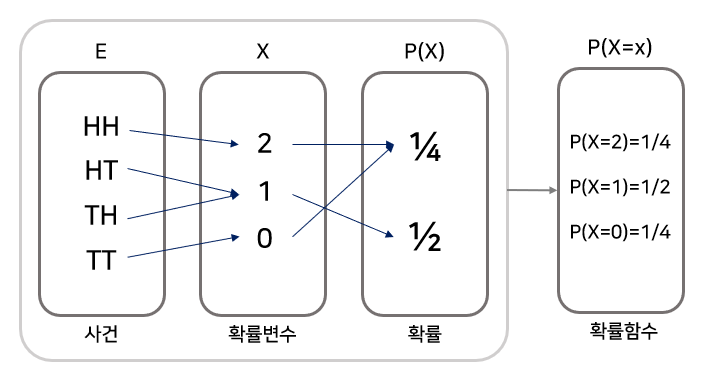
P( 0<X<3 ) = 1/4 + 2/4 = 3/4

이미지 출처 : [기초통계] 이산 확률변수 vs 연속 확률변수

연속확률변수

사람의 몸무게, 통학시간, 각 물질의 끓는 점 등과 같이 확률변수 X가 어떤 구간의 모든 실수값을 가질 때, 그 확률변수 X를 연속확률변수라고 한다.

확률밀도함수 (Probability density function)

연속확률변수 X에 대해서 함수 f(x) 가 아래의 조건을 만족하면 확률밀도함수라고 한다.

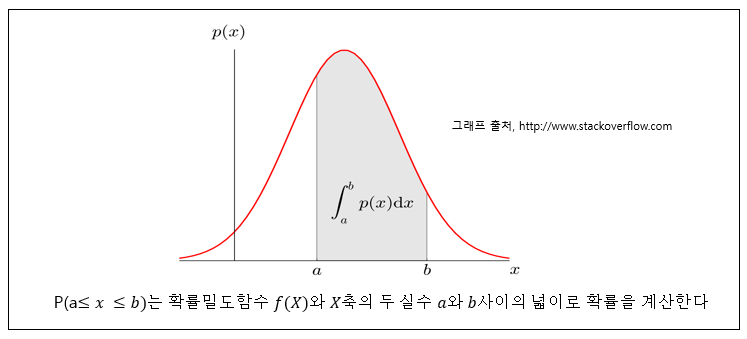
이미지 출처 : 확률밀도함수(Probability Density Function)

이산확률변수의 기대값

✒️ 예제

아래 표와 같이 상금이 걸려 있는 복권에서 상금의 평균을 구하시오

------------------------------------------------
|   상금  | 10,000 | 5,000 | 1,000 |   0  | 합계 |
------------------------------------------------
| 복권 수 |   1   |   5   |   15  |  29  |  50  |
------------------------------------------------

------------------------------------------------
|   X   | 10,000 | 5,000 | 1,000 |   0   | 합계 |
------------------------------------------------
| P(X)  |  1/50  |  5/50 | 15/50 | 29/50 |  1  |
------------------------------------------------

기댓값 : E(X) = (1000
*1/50) + (5000*5/50) + (1000*15/50) + (0 * 29/50) = 1000

: 확률변수 * 확률의 평균

복권을 한장을 구입할 때 기대할 수 있는 상금 : 1000
만약 복권 한장의 가격이 500원이면 살만 하나 1000원 보다 비싸면 확률적으로 안사는것이 낫다고 생각할 수 있다.