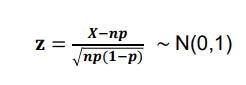이산확률변수(discrete random variable) : 확률변수 X가 셀 수 있는 값들로 구성되거나 일정 범위로 나타나는 경우
연속 확률 변수(continuous random variable) : 확률변수 X가 연속형 또는 무한대와 같이 셀 수 없는 경우
확률분포(probability distribution)
확률변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수
이산확률분포
📌 이산형균등분포 (discrete uniform distribution)
확률변수 X가 유한개이고, 모든 확률변수에 대하여 균일한 확률을 갖는 분포를 이산형균등분포라고 한다.
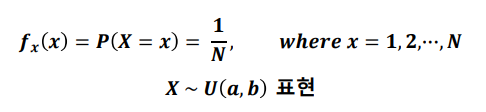
주사위를 한벌 굴려서 나오는 숫자를 확률 변수 X라고 하면, 확률변수 X는 아래와 같다.
---------------------------------------------
| X | 1 | 2 | 3 | 4 | 5 | 6 |
---------------------------------------------
| f(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
---------------------------------------------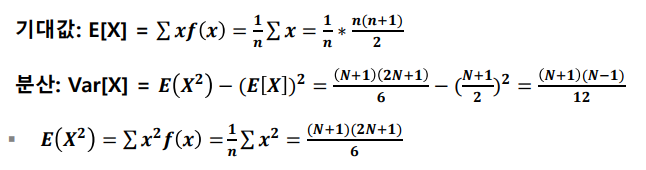
📌 베르누이 분포 (Bernoulli trial)
각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행을 베르누이 시행이라고 한다.
베르누이 시행에서 성공이 ‘1’, 실패가 ‘0’의 값을 갖을 때 확률 변수 X의 분포를 베르누이 분포(Bernoulli distribution)라고 하며 다음과 같이 정의함

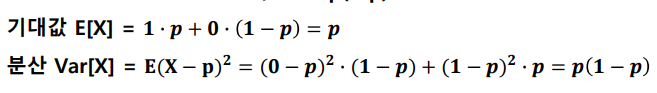
📑예제
3개 빨간공, 검은공 7개가 있는 주머니가 있다
검정공을 뽑을 시 성공, 빨강공을 뽑을 시 실패라고 가정한다
P(1) = 3/10 = p
P(0) = 7/10 = 1-p
E(X) = 1*P(1) + 0*p(0) = p
Var(X) = E(X^) - E(X)^
= 1^*p + 0^*(1-p) - p^
= p-p^
= p(1-p)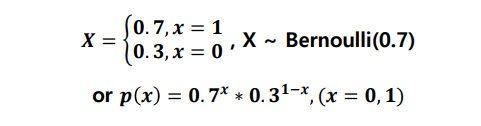
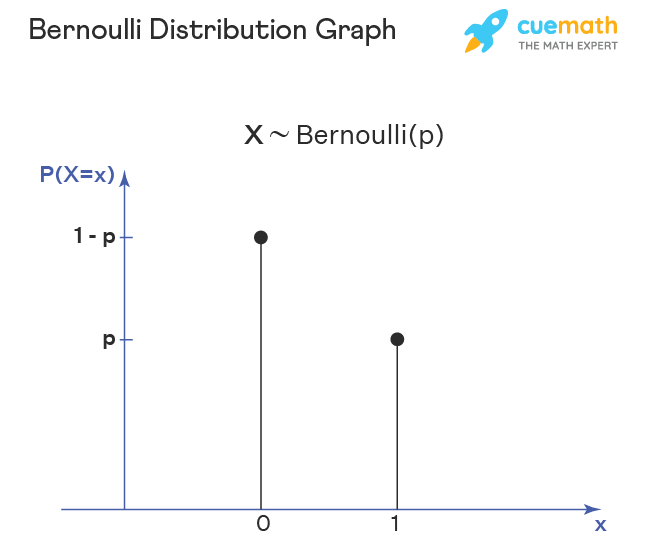
베르누이 분포 그래프
📌이항 분포 (Binomial distribution)
연속적으로 베르누이 시행을 거쳐 나타나는 확률 분포
서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
📑 예제
축구선수의 패널티킥 성공률이 80%일때, 10번 시행 시 성공횟수를 X라고 한다.
P(0) = 자유투가 성공하지 않을 확률 = 0.2^10
P(0) = 10C0 * (0.8^0 *0.2^10)
P(1) = 10C1 * (0.8 * 0.2^9)
P(2) = 10C2 * (0.8^2 * 0.2^8)
...
P(10) = 10C10 * (0.8^10 * 0.2^0)
P(X) = nCx * (p^x * (1-p)^(n-x))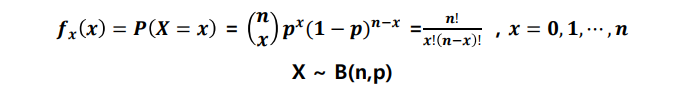
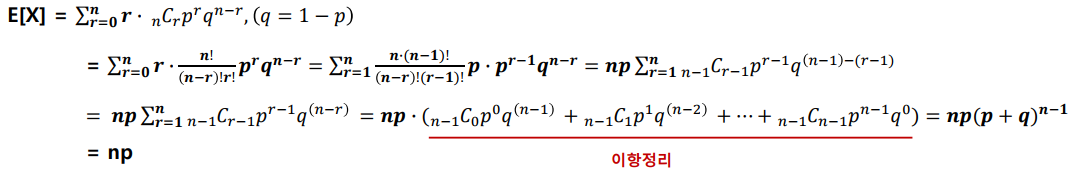
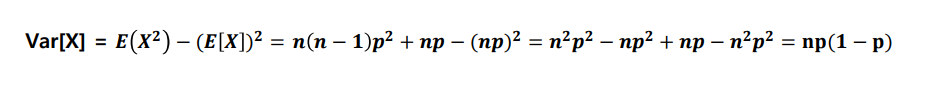
📑 예제
반도체 공장에서 불량이 발생할 확률이 10%라고 하자. 10개의 제품을 생성했을때 불량이 2개 이하일 확률을 구하시오
P(0) = 10C0 * 0.9^10
p(1) = 10C1 * 0.1^1 * 0.9^9
p(2) = 10C2 * 0.1^2 * 0.9^8
= 0.35 + 0.39 + 0.19
= 0.93 📌 기하 분포 (Geometric Distribution)
동일한 베르누이 분포를 따르는 시행의 독립적인 반복에서 처음으로 성공하기까지의 시도횟수를 확률변수로 가지는 분포
복권에 당첨될 확률이 5%일 때, 사람이 X번째로 복권을 사서 당첨될 확률을 P(X)라고 하자
P(1) = 0.05
P(2) = 0.95 * 0.05
P(3) = 0.95 * 0.95 * 0.05
P(X) = (p)*(1-p)^(x-1)
📑 예제
축구선수 손흥민의 필드골 성공 확률이 30%일 때, 5번째 슈팅에서 골을 넣을 확률 분포
(1-0.3)^4*0.3 = 0.07203
📌 음이항 분포 (Negative Binomial distribution)
기하분포는 성공확률이 p일 때, x번째 시행에서 첫번째 성공이 나올 확률을 P(X)라 했다.
P(X) = (p)*(1-p)^(x-1)
음이항분포는 여러 정의가 있다. 그 중 기하분포와 관련된 정의를 보자
성공확률이 p일 때, x번째 시행에서 K번째 성공이 나올 확률을 P(X)라 한다.
P(X) = x-1Ck-1 * p^k * (1-p) x-k
다음은 독립변수 , 종속변수, 상수에 따라 정의해보자. 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률 분포
전체 시행 횟수 : n, 성공횟수 : k, 실패횟수 : r
n = k + r
1) r이 정해지고, k가 변수인 경우 (가장 일반적으로 사용)
= r번의 실패가 나오기까지 성공이 k번일 확률
2) r이 정해지고, n이 변수인 경우 (r은 상수 k는 독립변수)
3) k가 정해지고, r이 변수인 경우
4) k가 정해지고, n이 변수인 경우
5) n이 정해지고, k 또는 r이 변수인 경우
📑 예제
농구 선수의 자유투 성공 확률이 30%일 때, 3번째 실패가 나올 때 까지 성공시킨 자유투가 X 번일 확률의 분포
P(0) = 3C3 * 0.7^3
P(1) = 3C1 * 0.3 * 0.7^3
P(2) = 4C2 * 0.3^2 * 0.7^3
r이 정해지고, k가 변수인 경우 (가장 일반적으로 사용)
= r번의 실패가 나오기까지 성공이 k번일 확률
f ( x ; r , p ) = P(X)
r번째 실패가 발생하기까지 성공은 x 번이라 정의한다.
r번째 실패 이전 횟수 : x + r - 1
p(x) = (x+r-1)Cx * p^x * (1-p)^r
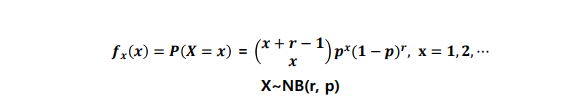
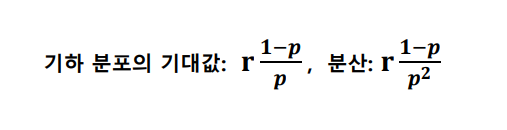
📌 포아송 분포 (Poisson distribution)
어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포
예시) 야구장에서 파울볼을 잡을 횟수, 버스 정류장에서 특정 버스가 5분 이내에 도착한 횟수, 책에서 발경되는 오타의 수
포아송 분포의 조건
1. 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예: 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정
2. 두 개 이상의 사건이 동시에 발생할 확률은 0에 가까움
3. 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적임
4. 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함
5. 포아송분포 확률 변수의 기댓값과 분산은 모두 λ 임
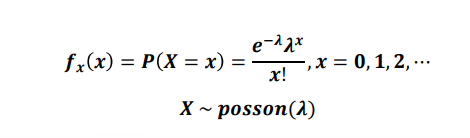
e = EXP( number ) 상수 e를 number만큼 거듭제곱한 값을 반환한다
λ : 사건의 평균 발생횟수
📑 예제
길냥이를 바주치는 평균 횟수가 3회라면 한번만 마주치는 확률은 무엇일까?
P(1) = (e^-3)(3^1) / 1!
야구장에서 경기당 홈런볼을 잡는 관객이 평균 3명 이라고 가정하자
- 오늘 경기에서 2명 이상이 홈런볼을 잡을 확률을 구하시오
λ = 3
P(X>=2) = 1 - (P(0) + P(1)
P(0) = (e^-3)(3^0)/0! + (e^-3)(3^1)/1! - 오늘과 내일 동안 경기에서 홈런볼을 잡지 못할 확률을 구하시오
(e^-3)(3^0)/0! * (e^-3)(3^0)/0! = (e^-6)(6^0) / 0! 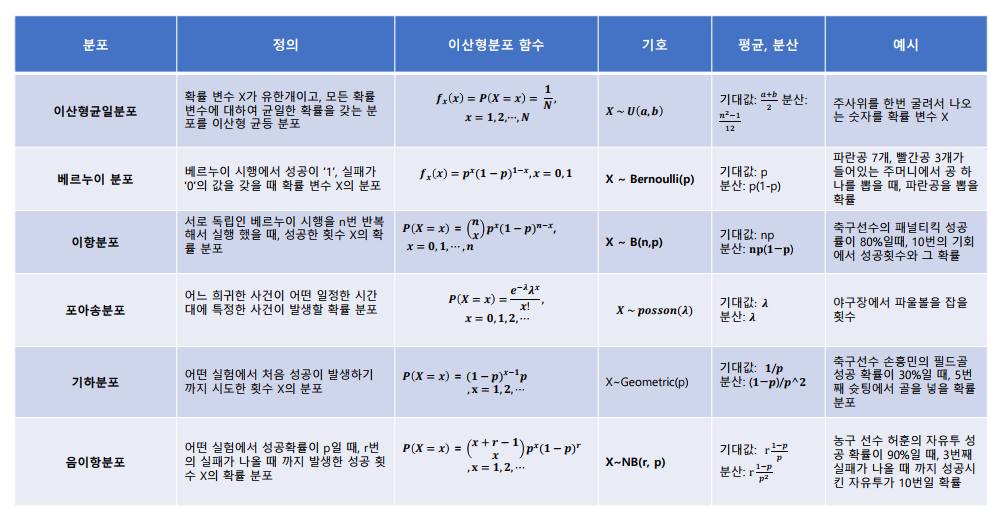
연속확률분포
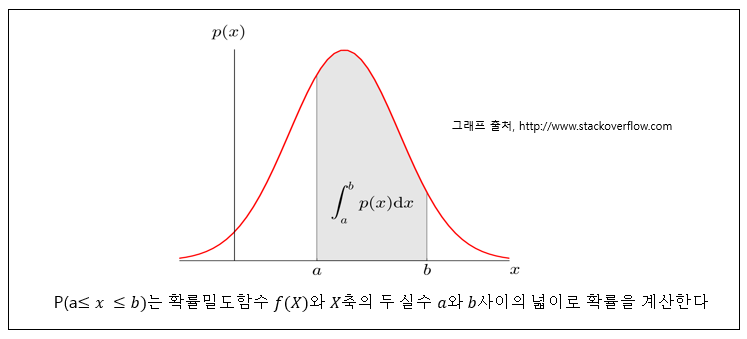
📌 확률밀도함수(probability density function)
연속형 확률 변수 X에 대해서 함수 f(x) 가 아래의 조건을 만족하면 확률밀도함수라고 함

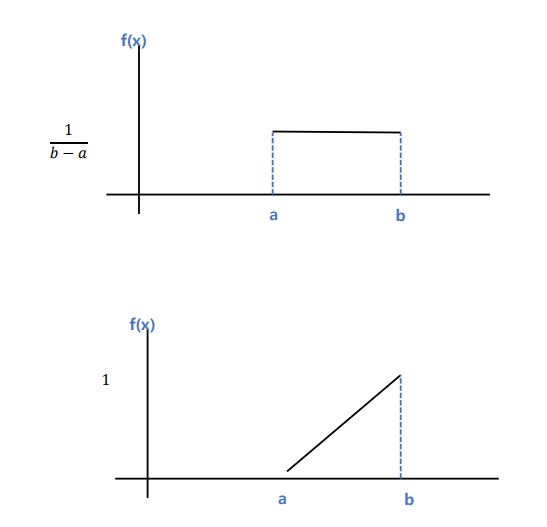
📌 균등분포 (uniform distribution)
모든 확률변수의 함수값이 동일한 분포
확률 변수가 X가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)를 갖는다.
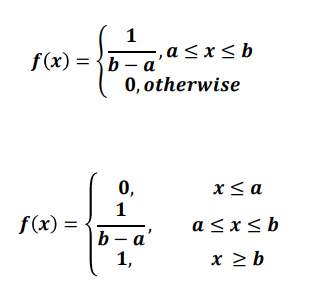
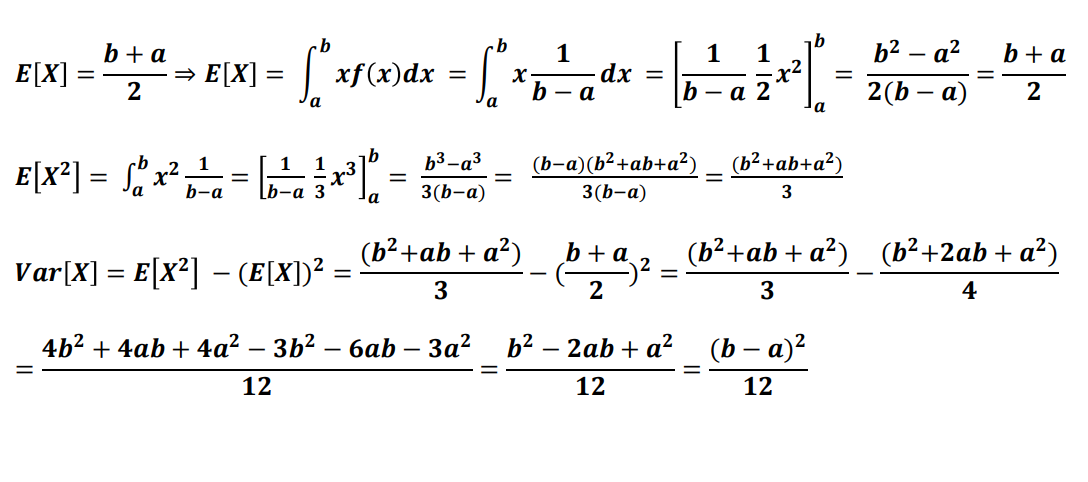
📑 예제
5분마자 한대씩 오는 버스가 있을 때, 버스를 기다리는 시간이 x분일 확률
x의 값은 셀 수 없다.
P(0<=x<=5) = k
|
|
|
k |--------
| ///// | >>> 넓이 = 1 -> k = 1/5
--------------
| 5
버스를 기다리는 시간이 0분에서 2분 사이일 확률
= 2/5
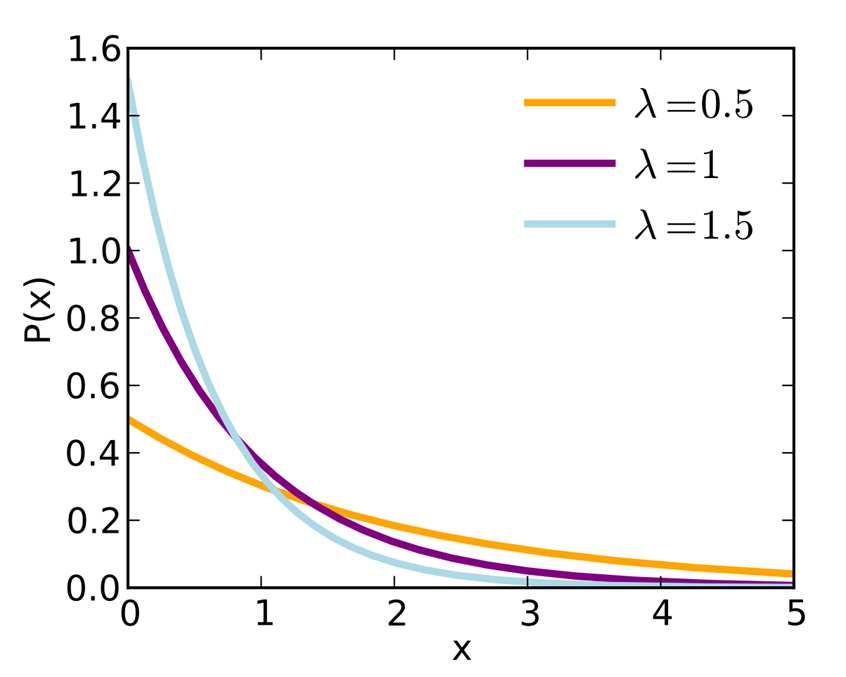
📌 지수분포
단위 시간당 발생할 확률 λ인 어떤 사건의 횟수가 포아송 분포를 따르다면, 어떤 사건이 처음 발생 할때까지 걸린 시간 확률 변수 X는 지수 분포임
예시)
1. 하루에 길냥이를 3번 마주칠 확률이 포아송분포라면, 길냥이를 마주칠때까지 걸리는 기간이 T일 이하일 확률이 지수분포
2. 버스 정류장에서 100번 버스가 도착하는 횟수가 포아송 분포를 따른다면, 첫 번째 버스가 도착할 때까지 대기 시간의 분포가 지수분포


📑 예제
하루동안 길냥이를 x회 만날 확률은?
λ = 3
P(x) = (3^x)(e^-3)/x!길냥이를 마주칠때까지 걸리는 기간이 5일이하일 확률
=> 1 - (5일동안 길냥이를 마주치질않을 확률)
p(0)^5 = ((3^0)(e^-3)/0!)^5 = (e^-3)^5
📑 예시
버스 정류장에 A버스가 평균 시간당 6대가 정차한다고 가정 하자
1) 10분 이상 대기할 확률은?
분당 버스횟수 평균 : λ = 6/60
p(x) = (1/10^x)(e^-(1/10))/x!
1 - p(0)^10
= 1-( (e^-(1/10)) )^10
= 1-(e^-1)2) 10분에서 20분 대기할 확률은?
p(0)^20 - p(0)^10 = 1-(e^-2) - 1-(e^-1)누적분포함수 (cumulative density function)

지수분포의 무기억성 (Memoryless Property)
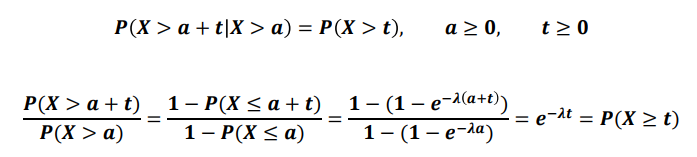
어떤 시점 부터 소요되는 시간은 과거 시간에 영향을 받지 않음
예시) 버스를 기다리는 대기시간은 먼저 기다린 사람과 확률이 같음
전구를 한달 동안 사용 했을 때 남은 수명은 한달 간 사용했던 영향을 받지 않음, 즉 새전구와 한달 간 사용한 전구의 남은 수명은
같다고 생각함
📌 정규분포 (normal distribution)
정규 분포는 19세기 최대 수학자라고 불리는 독일의 가우스에 의해 제시된 것으로 가우스 분포라고도 함
확률 밀도 함수는 확률 변수 X가 평균이 μ 이고, 분산이 σ² 인 정규분포를 따를 때 아래와 같음
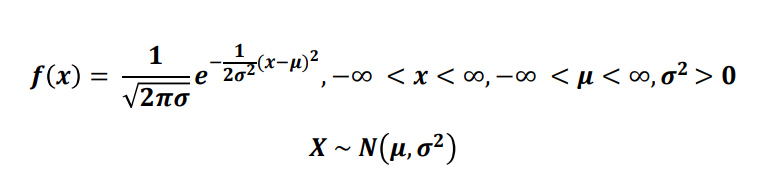
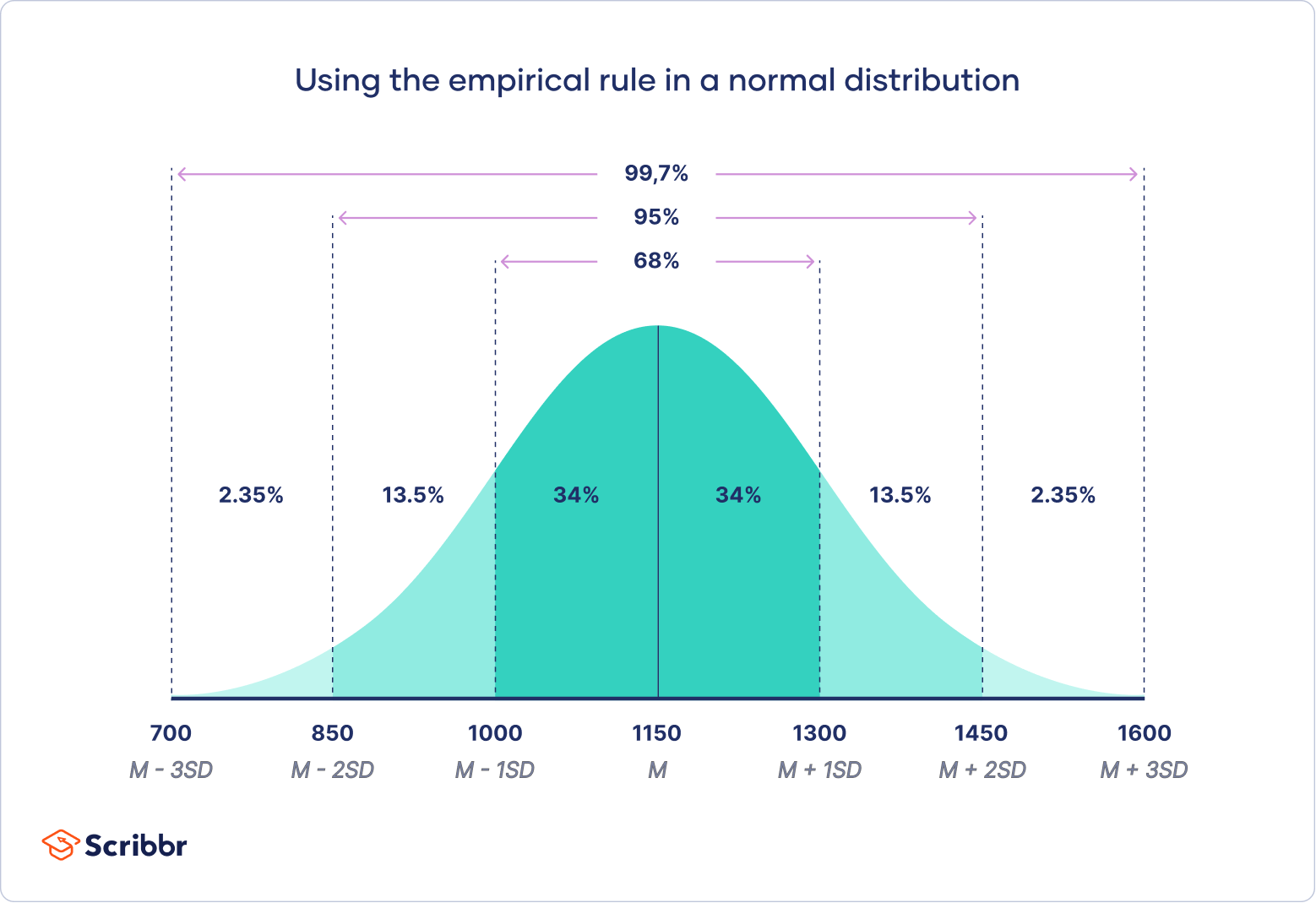
_이미지 출처 : https://www.scribbr.com/statistics/normal-distribution/

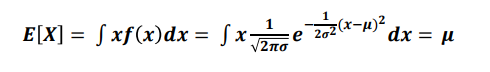
표준정규분포
확률변수 X ~ N(μ,σ²) 정규 분포를 따르고, 확률변수 Z = X- μ / σ 라고 할때 확률변수 Z~N(0,1)
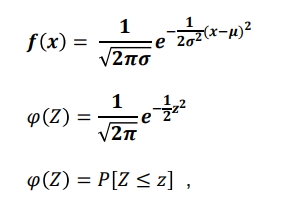
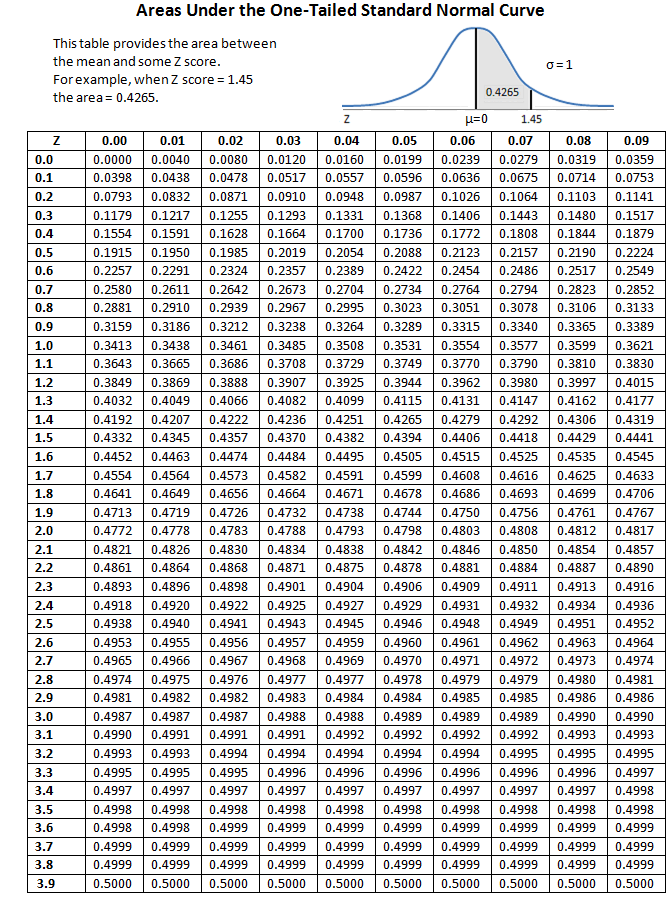
이미지 출처 : Basic Statistics and Data Analysis
예시1) P[Z ≤ 1.96] = 0.975
예시2) P[Z ≤ -1.96] = 1 − P[Z ≤ 1.96] = 0.025
예시3) P[0.5 ≤ Z ≤ 1.96] = 0.975 − 0.6915 = 0.28354
정규분포의 성질

예시) X ~ N(100,100²),일 떄,P[ 100 ≤ X ≤ 110] 을 구하시오
이항분포의 정규 근사