TIL(4W2D)[Matplotlib] 데이터 시각화 총정리

최유정·2025년 1월 7일

[강의] 데이터 전처리 & 시각화

목록 보기

4/4

1. Matplotlib.pyplot

: 시각화를 위한 라이브러리 중 하나. 다양한 종류의 그래프를 생성하기 위한 도구를 제공.

import matplotlib.pyplot as plt

2D 그래픽 생성에 주로 사용.
다양한 시각화 방식 지원.
다양한 스타일로 튜닝 가능.

2. 그래프 그리기

(cf) 도구

1. 축

x, y 인수: 각각 x축, y축에 해당하는 열을 지정.
title(): 그래프 제목
xlable(): x축 레이블
ylable(): x축 레이블

2. 범례

legend(): 그래프의 범례를 추가(loc=''을 넣어서 위치 조정도 가능)
label: 그래프 생성 코드에 바로 넣어서 범례 추가 가능.

3. 스타일

color
linestyle
marker
etc.

4. 텍스트

plt.text(x좌표, y좌표, 'text', fontsize=10)

1. Line plot(선 그래프)

: 데이터 간의 연속적인 관계를 시각화하는데 적합. 주로 시간의 흐름에 따른 데이터의 변화를 보여줌.

import pandas as pd
import matplotlib.pyplot as plt

# 데이터프레임 생성
data = {'날짜': ['2023-01-01', '2023-01-02', '2023-01-03'],
        '값': [10, 15, 8]}
df = pd.DataFrame(data)

# '날짜'를 날짜 형식으로 변환
df['날짜'] = pd.to_datetime(df['날짜'])

# 선 그래프 작성
plt.plot(df['날짜'], df['값'])
plt.xlabel('날짜')
plt.ylabel('값')
plt.title('선 그래프 예시')
plt.show()

x축은 같고 y축에 넣는 열이 다르면, 복합 그래프로 그릴 수 있음.

# 1) 날짜별 집계
# your code here
grouped_df2=df.groupby('Date').agg({'Production':'sum', 'Defects':'sum'})

grouped_df2

x= grouped_df2.index
y1= grouped_df2['Production']
y2= grouped_df2['Defects']

# 2) 선 그래프(Line Chart) 작성
plt.figure(figsize=(12,6))
bar1=plt.plot(x, y1, marker='o',label='Production')
bar2=plt.plot(x, y2, marker='x', label='Defects')
plt.title('Daily Trends: Production and Defects')
plt.xlabel('Date')
plt.ylabel('Count')
plt.legend(['Total production', 'Total defects'])
plt.grid(True)

2. Bar plot(막대 그래프)

: 범주형 데이터를 나타내며, 각각의 값을 비교할 때 사용.

# 데이터프레임 생성
data = {'도시': ['서울', '부산', '대구', '인천'],
        '인구': [990, 350, 250, 290]}
df = pd.DataFrame(data)

# 막대 그래프 작성
plt.bar(df['도시'], df['인구'])
plt.xlabel('도시')
plt.ylabel('인구')
plt.title('막대 그래프 예시')
plt.show()

막대 그래프의 x좌표는 막대의 가운데 축에 해당하는 x값을 기본으로 함 ==> width를 조정해서 하나의 범주에 막대 여러 개(bar나란히)를 같이 그릴 수도 있음.

import numpy as np
import matplotlib.pyplot as plt

# 예시 데이터 (df 대신 사용)
labels = ['Line1', 'Line2', 'Line3']
y1 = [100, 150, 120]  # Production
y2 = [5, 8, 12]       # Defects

# X좌표 생성을 위해 numpy의 arange 사용
x = np.arange(len(labels))  # [0, 1, 2, ...] 형태가 됨
width = 0.4  # 막대 너비

plt.bar(x - width/2, y1, width=width, label='Production')
plt.bar(x + width/2, y2, width=width, label='Defects')

# x축 눈금과 레이블 설정
plt.xticks(x, labels, rotation=0)

plt.title('Total Production and Defects by Line')
plt.xlabel('Line')
plt.ylabel('Count')
plt.legend()
plt.grid(axis='y')
plt.show()

또는 x좌표를 막대 그래프의 왼쪽 모서리로 맞춰 조정할 수도 있음.

plt.bar(x, y, align='edge')

3. Histogram(히스토그램)

: 연속된 데이터의 분포를 보여줌. 주로 데이터의 빈도를 시각화해 데이터 분포에 대한 이해를 도움.

* 주의점
: 다중 히스토그램을 그릴 때에는 데이터 개수와 구간의 개수를 맞춰줘야 종 모양의 대칭 구조를 얻을 수 있음

bins or binning= 데이터가 속할 구간의 개수
alpha = 투명도

import matplotlib.pyplot as plt
import numpy as np

# 데이터 생성 (랜덤 데이터)
data = np.random.randn(1000)

# 히스토그램 그리기
plt.hist(data, bins=30)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Histogram')
plt.show()

4. Pie(파이 차트)

: 백분율로 카테고리별 비율을 나타내서 비교할 때 사용.

autopct = 각 값을 숫자로 나타낼 때 표현과 관련된 함수
- % 형식 지정자를 사용하여 표시 형식을 설정합니다.
  1) %1.1f%% : 소수점 첫째 자리까지 표시 (예: 30.0%)
  2) %1.0f%% : 소수점 없이 정수로 표시 (예: 30%)
  3) %1.2f%% : 소수점 둘째 자리까지 표시 (예: 30.00%)
startangle = 파이 차트의 회전 정도

import matplotlib.pyplot as plt

# 데이터 생성
sizes = [30, 20, 25, 15, 10]
labels = ['A', 'B', 'C', 'D', 'E']

# 원 그래프 그리기
plt.pie(sizes, labels=labels, autopct='%1.1f%%')
plt.title('Pie Chart')
plt.show()

구간을 나눠서 새롭게 컬럼을 만들어내서 파이 차트를 그릴 수도 있음.
! pandas cut 함수 참고 자료_블로그

# 라이브러리 불러오기
import matplotlib.pyplot as plt
import pandas as pd

# 구간(binning)과 라벨 설정
binning= [0, 0.015, 0.02, 0.025]
label = ['Low (<= 0.015)', 'Medium (0.015-0.02)', 'High (> 0.02)']

# 결함률 데이터를 범주화하여 새로운 컬럼 생성
data_cleaned['defect_rate_category']=pd.cut(data_cleaned['defect_rate'], bins=binning, labels=label)
vc=data_cleaned['defect_rate_category'].value_counts()

# 파이 차트 생성
plt.figure(figsize=(8,8))
plt.pie(vc,labels=label,
        autopct='%1.1f%%',
        startangle=140,
        colors=['#66b3ff', '#99ff99', '#ffcc99'])

# 차트 제목 설정
plt.title("Defect Rate Categories")
# 차트 표시
plt.show()

5. Box plot(박스 플롯)

: 데이터의 분포와 이상치를 시각적으로 보여줌. [중앙값, 사분위수, 최솟값, 최댓값, 이상치 등]을 제공하여 데이터의 '통계적' 특성을 파악하는 데 사용.

1. 박스 플롯의 구성 요소

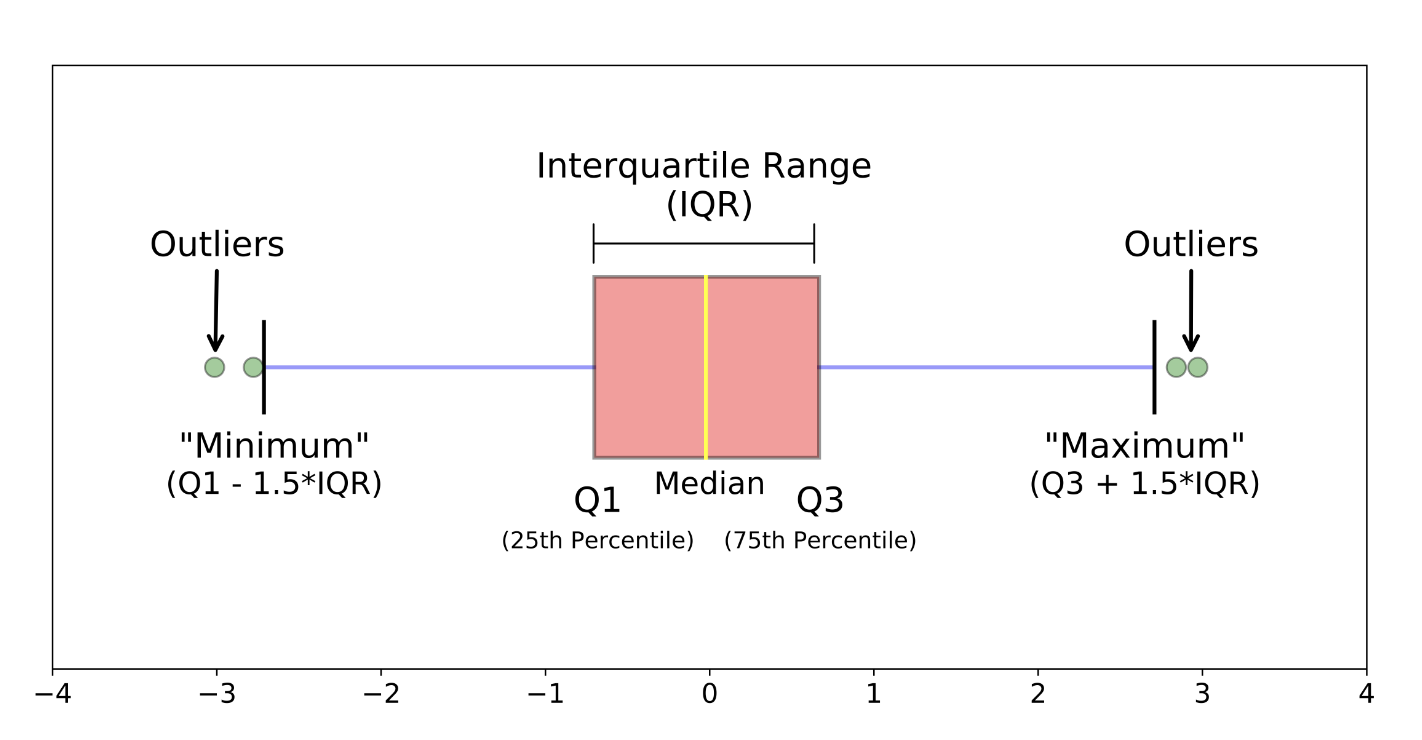
1. 상자(Box)

: 사분위수(Interquartile Range, IQR) + 데이터 중앙값(median, Q2)

IQR = Q3 - Q1
- Q1(25%) : 상자 아래 끝 or 왼쪽 끝
- Q3(75%) : 상자 위 끝 or 오른쪽 끝
median(Q2) : 상자 속 위치한 선

2. 수염(Whisker)

: 상자의 양쪽으로 연장되는 선. 일반적으로 IQR의 1.5배 범위로 계산.

3. 최솟값, 최댓값(Minimum, Maximum)

: 수염의 각 끝에 해당하는 값.

min : Q1 - 1.5 * IQR
max : Q3 + 1.5 * IQR

4. 이상치(Outliar)

: 수염을 벗어나는 범위에 해당하는 값. 일반적인 범위를 벗어나는 값으로 독립적으로 표시.

import matplotlib.pyplot as plt
import numpy as np

# 데이터 생성
np.random.seed(10)
data = [np.random.normal(0, std, 100) for std in range(1, 4)]

# 박스 플롯 그리기
plt.boxplot(data)
plt.xlabel('Data')
plt.ylabel('Value')
plt.title('Box Plot')
plt.show()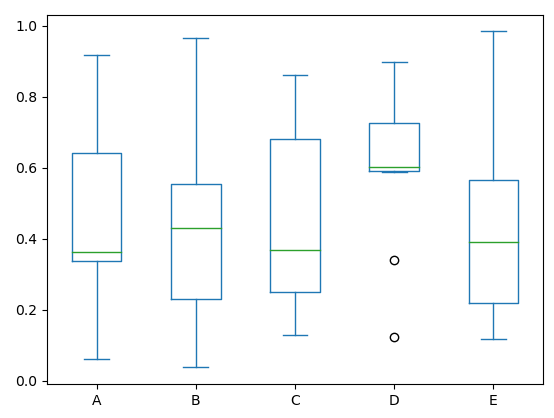

6. Scatter plot(산점도)

: 두 변수 간의 상관 관계를 점으로 표시해 보여주는 그래프.

import matplotlib.pyplot as plt

# 데이터 생성
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]

# 산점도 그리기
plt.scatter(x, y)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('Scatter Plot')
plt.show()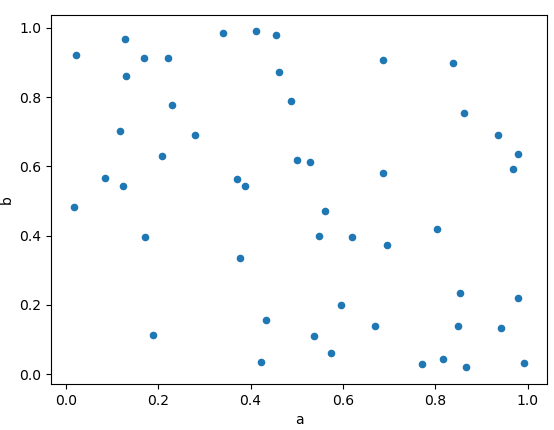

1. 상관관계 확인

1.양의 상관관계

: 점들이 오른쪽 위 방향으로 일직선으로 분포되어 있을 때. 즉, 하나의 변수가 증가할 때 다른 변수도 증가하는 경향이 있음.

2. 음의 상관관계

: 점들이 왼쪽 위 방향으로 일직선으로 분포되어 있을 때. 하나의 변수가 증가할 때 다른 변수는 감소하는 경향이 있음.

3. 무상관 관계

: 점들이 어떤 방향으로도 일직선으로 분포하지 않고 무작위로 퍼져 있을 때. 즉, 두 변수 간에는 상관관계가 거의 없는 것으로 보임.

2. 상관관계의 강도 확인

1. 점들의 모임

: 점들이 더 밀집된 곳은 상관관계가 높음.

2. 점들의 방향성

: 일직선에 가까운 분포일수록 상관관계가 강할 가능성이 높음.

3. 상관계수 계산

: 피어슨 상관계수와 같은 통계적 방법을 사용하여 상관관계의 정도를 수치적으로 계산 가능.

3. 피어슨 상관계수(Pearson correlation coefficient)

: 두 변수 간의 선형적인 관계를 측정하기 위한 통계적인 방법 중 하나

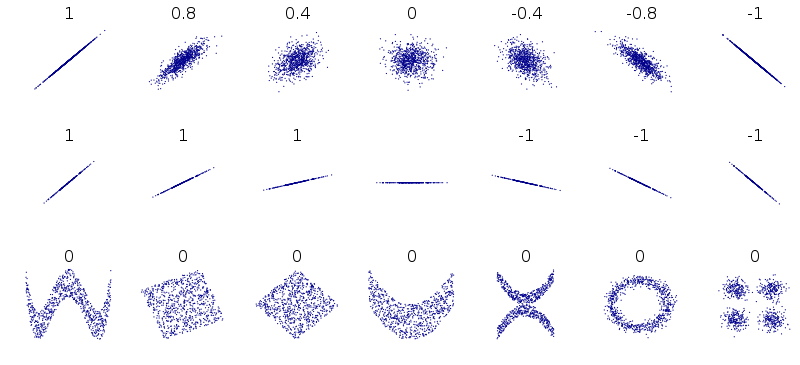
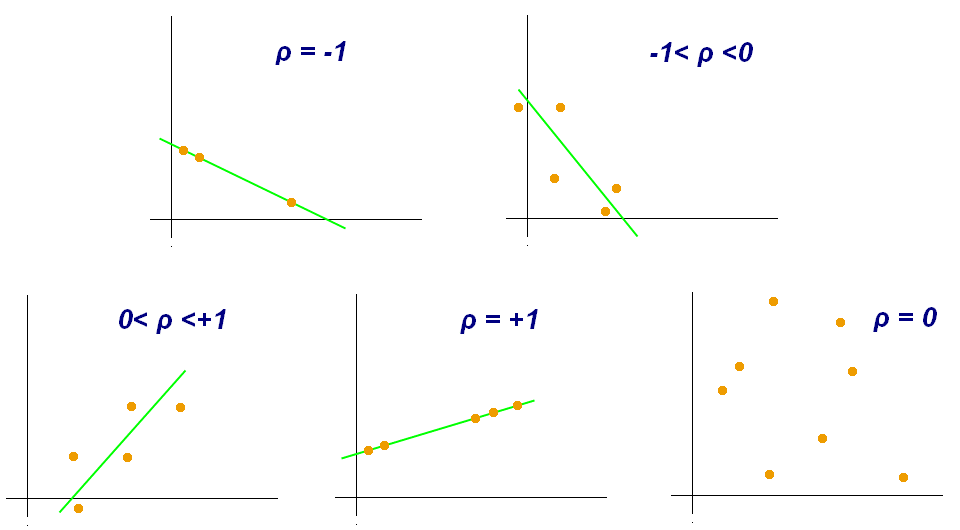
범위: -1 < p < 1
- 양의 상관관계: 1에 가까울수록 강한 양의 선형관계
- 음의 상관관계: -1에 가까울수록 강한 음의 선형관계
- 무상관관계: 0에 가까울수록 약한 관계

*주의점
: 강한 상관관계를 가진다고 해서, 꼭 인과관계인 것은 아님.

3. 정리

그래프 유형

그래프 유형	자료 유형	특징
Line plot	연속형 데이터	데이터의 변화 및 추이를 시각화
Bar plot	범주형 데이터	카테고리 별 값의 크기를 시각적으로 비교
Histogram	연속형 데이터	데이터 분포, 빈도, 패턴 등을 이해
Pie chart	범주형 데이터의 비율	범주별 상대적 비율을 부채꼴 모양으로 시각화
Box plot	연속형 데이터의 분포	중앙값, 사분위수, 최소값, 최대값, 이상치 확인
scatter plot	두 변수 간의 관계	변수 간의 관계, 군집, 이상치 등 확인

최유정

이전 포스트