graphSAGE 논문 요약 및 코드 리뷰

graphSAGE-pytorch

• arguments

parser.add_argument('--dataSet', type=str, default='cora')
parser.add_argument('--agg_func', type=str, default='MEAN')
parser.add_argument('--epochs', type=int, default=50)
parser.add_argument('--b_sz', type=int, default=20)
parser.add_argument('--seed', type=int, default=824)
parser.add_argument('--cuda', action='store_true',
					help='use CUDA')
parser.add_argument('--gcn', action='store_true')
parser.add_argument('--learn_method', type=str, default='sup')
parser.add_argument('--unsup_loss', type=str, default='normal')
parser.add_argument('--max_vali_f1', type=float, default=0)
parser.add_argument('--name', type=str, default='debug')
parser.add_argument('--config', type=str, default='./src/experiments.conf')

• config

file_path {
	workdir = ./
	cora_content = ${file_path.workdir}cora/cora.content
	cora_cite = ${file_path.workdir}cora/cora.cites
	pubmed_paper = ${file_path.workdir}pubmed-data/Pubmed-Diabetes.NODE.paper.tab
	pubmed_cites = ${file_path.workdir}pubmed-data/Pubmed-Diabetes.DIRECTED.cites.tab
}


setting {
	num_layers = 2
	hidden_emb_size = 128
}

데이터 셋이나 데이터 로더 등등은 이전과 크게 다를 바가 없으므로 생략한다.
main.py의 training 과정을 보면

graphSage = GraphSage(config['setting.num_layers'], features.size(1), config['setting.hidden_emb_size'], features, getattr(dataCenter, ds+'_adj_lists'), device, gcn=args.gcn, agg_func=args.agg_func)
num_labels = len(set(getattr(dataCenter, ds+'_labels')))
classification = Classification(config['setting.hidden_emb_size'], num_labels)
unsupervised_loss = UnsupervisedLoss(getattr(dataCenter, ds+'_adj_lists'), getattr(dataCenter, ds+'_train'), device)

먼저 graphSage와 Classification 모델을 선언한다.
argument를 확인해보면,
num_layer가 논문에서의 K이고(depth),
input_size가 dataset에서 feature의 개수, out_size가 embedding_dim이라고 볼 수 있을 것 같다.
graphSage 모델은 좀 이따 보기로 하고, Classification 모델만 먼저 보면

self.layer = nn.Sequential(
						nn.Linear(emb_size, num_classes)	  
						#nn.ReLU()
					)
def forward(self, embeds):
	logists = torch.log_softmax(self.layer(embeds), 1)
	return logists

logistic regression으로 embedding을 label로 분류하는 아주 간단한 모델이다.

UnsupervisedLoss도 나중에 설명하기로 한다.

for epoch in range(args.epochs):
	print('----------------------EPOCH %d-----------------------' % epoch)
	graphSage, classification = apply_model(dataCenter, ds, graphSage, classification, unsupervised_loss, args.b_sz, args.unsup_loss, device, args.learn_method)
	if (epoch+1) % 2 == 0 and args.learn_method == 'unsup':
		classification, args.max_vali_f1 = train_classification(dataCenter, graphSage, classification, ds, device, args.max_vali_f1, args.name)
	if args.learn_method != 'unsup':
		args.max_vali_f1 = evaluate(dataCenter, ds, graphSage, classification, device, args.max_vali_f1, args.name, epoch)

이후 모델을 학습하고 evaluate로 평가를 하는 모습을 볼 수 있다. 또한 unsupervised의 경우에는 2 epoch마다 classification을 학습하는 모습을 확인할 수 있다.
apply_model의 argument로는 batch_size와 unsup_loss 등이 들어감을 확인 가능하다.

if unsup_loss == 'margin':
	num_neg = 6
elif unsup_loss == 'normal':
	num_neg = 100
    
models = [graphSage, classification]
params = []
for model in models:
	for param in model.parameters():
		if param.requires_grad:
			params.append(param)
optimizer = torch.optim.SGD(params, lr=0.7)

apply_model 코드를 보면, unsup_loss의 종류에 따라 num_neg를 다르게 두는 것을 확인 가능하다. 또한 graphSage 모델과 Classification 모델의 parameter를 한 list에 합쳐 이를 SGD optimizer에 넣어주는 것을 확인 가능하다.

batches = math.ceil(len(train_nodes) / b_sz)
for index in range(batches):
	nodes_batch = train_nodes[index*b_sz:(index+1)*b_sz]
nodes_batch = np.asarray(list(unsupervised_loss.extend_nodes(nodes_batch, num_neg=num_neg)))

그 후 batch_size로 train 데이터를 나눠준 후에 나눠진 nodes를 extend_nodes 메소드에 넘기는 것을 알 수 있다.

def extend_nodes(self, nodes, num_neg=6):
	self.positive_pairs = []
	self.node_positive_pairs = {}
	self.negtive_pairs = []
	self.node_negtive_pairs = {}

	self.target_nodes = nodes
	self.get_positive_nodes(nodes)
	# print(self.positive_pairs)
	self.get_negtive_nodes(nodes, num_neg)
	# print(self.negtive_pairs)
	self.unique_nodes_batch = list(set([i for x in self.positive_pairs for i in x]) | set([i for x in self.negtive_pairs for i in x]))
	assert set(self.target_nodes) < set(self.unique_nodes_batch)
	return self.unique_nodes_batch

extend_nodes는 unique한 positive_pairs와 negative_pairs를 구해 합친 후에 반환한다.

def get_positive_nodes(self, nodes):
	return self._run_random_walks(nodes)

def _run_random_walks(self, nodes):
	for node in nodes:
		if len(self.adj_lists[int(node)]) == 0:
			continue
		cur_pairs = []
		for i in range(self.N_WALKS):
			curr_node = node
			for j in range(self.WALK_LEN):
				neighs = self.adj_lists[int(curr_node)]
				next_node = random.choice(list(neighs))
				# self co-occurrences are useless
				if next_node != node and next_node in self.train_nodes:
					self.positive_pairs.append((node,next_node))
					cur_pairs.append((node,next_node))
				curr_node = next_node

		self.node_positive_pairs[node] = cur_pairs
	return self.positive_pairs

get_positive_nodes는 nodes를 받아 run_random_works를 실행하게 되고, run_random_walks는 node를 순회하며 N_WALKS = 6, WALK_LEN = 1로 positive nodes pair를 만들게 된다.
이 결과로 self.positive_pairs는 nodes의 node와 연결된 다른 node를 node마다 N_WALKS개 만큼 sampling하는 결과를 가져온다.

def get_negtive_nodes(self, nodes, num_neg):
	for node in nodes:
		neighbors = set([node])
		frontier = set([node])
		for i in range(self.N_WALK_LEN):
			current = set()
			for outer in frontier:
				current |= self.adj_lists[int(outer)]
			frontier = current - neighbors
			neighbors |= current
		far_nodes = set(self.train_nodes) - neighbors
		neg_samples = random.sample(far_nodes, num_neg) if num_neg < len(far_nodes) else far_nodes
		self.negtive_pairs.extend([(node, neg_node) for neg_node in neg_samples])
		self.node_negtive_pairs[node] = [(node, neg_node) for neg_node in neg_samples]
	return self.negtive_pairs

N_WALK_LEN = 5로 for문을 실행하며 neighbors은 for문이 지날 수록 더 많은 nodes를 가지게 되어 결과적으로 N_WALK_LEN까지 떨어진 neighbor을 모두 가지게 된다.
far_nodes는 전체 node에서 neighbors를 빼므로 node에서 N_WALK_LEN의 depth만으로 도달할 수 없는 node들만을 가지게 된다. 즉 이 코드에선 nodes로부터 depth가 6 이상인 노드들을 가지게 된다.
따라서 far_nodes에서 num_negs만큼 랜덤으로 sampling하면 negative nodes가 선별 되게 된다.

visited_nodes |= set(nodes_batch)
labels_batch = labels[nodes_batch]
embs_batch = graphSage(nodes_batch)

이 후 이 nodes들을 visited_nodes에 추가하고, 이에 대해 labels를 가져온다.
nodes_batch를 graphSage 모델에 넣어 이에 대한 embedding을 생성하게 된다.

if learn_method == 'sup':
	# superivsed learning
	logists = classification(embs_batch)
	loss_sup = -torch.sum(logists[range(logists.size(0)), labels_batch], 0)
	loss_sup /= len(nodes_batch)
	loss = loss_sup

만약 learn_method가 supervised라면 embeddings를 classification으로 분류하고, 분류된 logists의 각 row, 즉 한 node에 대한 label 예측값에서 실제 label인 부분만을 sum한다. 즉 1번째 노드의 실제 label이 0이었고, 그 node의 softmax 값이 [0.5, 0.2, 0.3] 이었다면 0.5만을 가져오고 이런 식으로 batch의 모든 노드들의 값을 가져와 더하게 된다.
이후 nodes_batch의 크기에 따라 loss가 정해지지 않도록 nodes_batch의 크기로 나눠주게 된다.

else:
	if unsup_loss == 'margin':
		loss_net = unsupervised_loss.get_loss_margin(embs_batch, nodes_batch)
	elif unsup_loss == 'normal':
		loss_net = unsupervised_loss.get_loss_sage(embs_batch, nodes_batch)
	loss = loss_net

unsupervised learning의 경우엔 margin과 normal로 나눠 계산하는데,

def get_loss_margin(self, embeddings, nodes):
	assert len(embeddings) == len(self.unique_nodes_batch)
	assert False not in [nodes[i]==self.unique_nodes_batch[i] for i in range(len(nodes))]
	node2index = {n:i for i,n in enumerate(self.unique_nodes_batch)}

self.unique_nodes_batch와 embedding의 개수, nodes_batch[i]와 unique_nodes_batch[i]가 같은 지 비교한다. 당연히 위의 extend_nodes에서 unique_nodes_batch를 반환하고 이를 node_batch로 이용해 embs_batch를 구했기 때문에 같아야 정상이다.
이 후 unique_nodes_batch에 index매겨 node to index를 만든다.

for node in self.node_positive_pairs:
	pps = self.node_positive_pairs[node]
	nps = self.node_negtive_pairs[node]

이 후 node_positive_pairs의 node들을 이용하는데, 이 때 node_positive_pairs는 원래 batch node(처음에 batch_size에 의해 가져온 노드)들을 포함하고 있다.
즉 batch의 node들에 대해 positive_pairs와 negative_pairs를 가져오게 된다.

indexs = [list(x) for x in zip(*pps)]
node_indexs = [node2index[x] for x in indexs[0]]
neighb_indexs = [node2index[x] for x in indexs[1]]
pos_score = F.cosine_similarity(embeddings[node_indexs], embeddings[neighb_indexs])
pos_score, _ = torch.min(torch.log(torch.sigmoid(pos_score)), 0)

위 코드는 본 node와 positive한 neighbor의 embedding끼리 cosine similarity를 구하게 된다. 즉 두 embedding끼리 얼마나 비슷한지 구한다. 그리고 이를 sigmoid -> log를 하여 가장 낮은 값을 pos_score로 한다.

indexs = [list(x) for x in zip(*nps)]
node_indexs = [node2index[x] for x in indexs[0]]
neighb_indexs = [node2index[x] for x in indexs[1]]
neg_score = F.cosine_similarity(embeddings[node_indexs], embeddings[neighb_indexs])
neg_score, _ = torch.max(torch.log(torch.sigmoid(neg_score)), 0)

neg_score도 같은 방식으로 구하되 이번엔 max값으로 neg_score로 한다.
즉 pos에 대해서는 가장 비슷하지 않은 것을 기준으로 하고, neg에 대해서는 가장 비슷한 것을 기준으로 한다는 것이다.

nodes_score.append(torch.max(torch.tensor(0.0).to(self.device), neg_score-pos_score+self.MARGIN).view(1,-1))

이 후 전체 score는 neg_score에 pos_score를 뺀 후 margin을 넣은 값을 한다.(self.MARGIN = 3)
loss는 낮아야 하므로 결과적으로 pos_score는 최대한 높이고, neg_score는 최대한 낮추는 방식으로 training을 하게 된다.

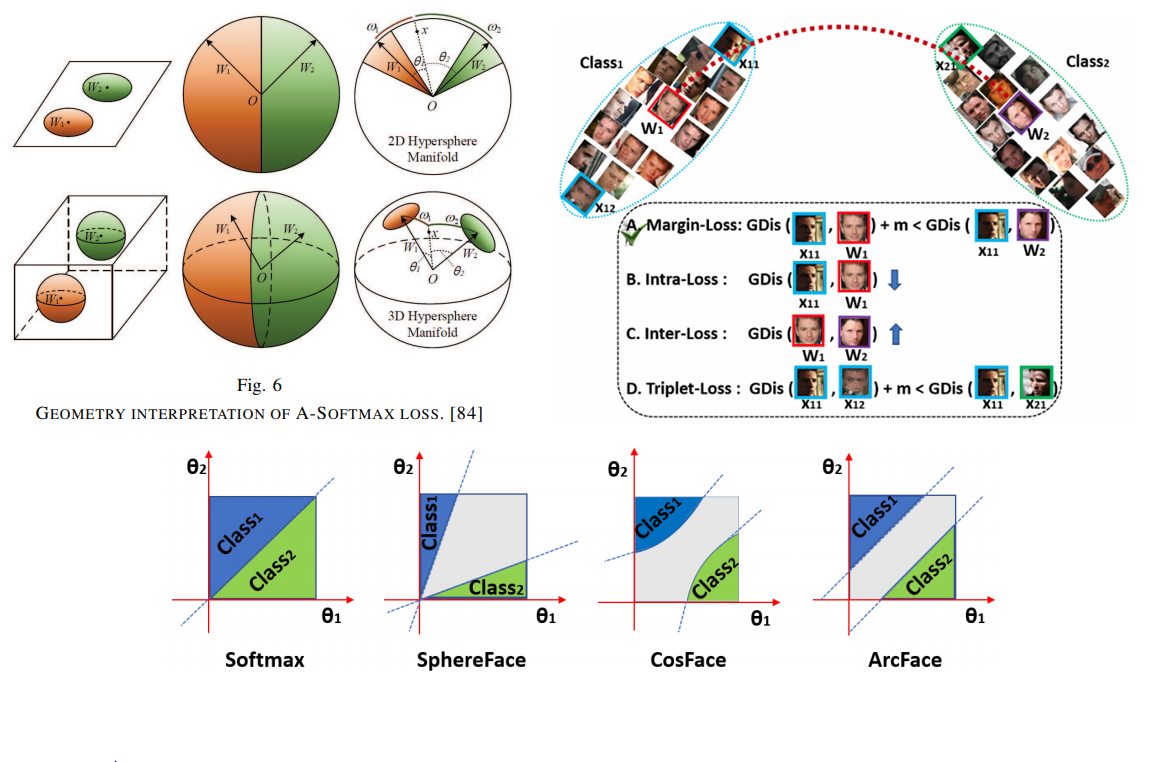
cosine similiarity = 1 - cosine distance이므로 이 식은 1 - neg dist - 1 + pos dist + margin = pos dist + margin - neg dist가 된다. 즉 pos dist를 줄이고 neg dist를 높이되 이 차이가 margin 이상으로는 되지 않도록 조절하는 느낌으로 보인다.
Unsupevised learning을 제대로 해본 적이 없어서 이 부분에 대해선 추후에 따로 공부하면 좋을 것 같다.

loss = torch.mean(torch.cat(nodes_score, 0),0)
return loss

각 node에 대해 nodes_score를 계산한 후에 이를 평균내어 loss로 삼게된다.

결과적으로 unsupervised learning에선 자신과 관계있는(WALK_LEN의 범위 안에 있는) 노드와 embedding을 최대한 일치시키고, 자신과 먼(N_WALK_LEN보다 더 떨어진) 노드들의 embedding과는 최대한 다르도록 만드는 것이 목표라고 할 수 있다.

normal 방식도 거의 비슷하지만 score를 구하는 방식이 약간 다르다.

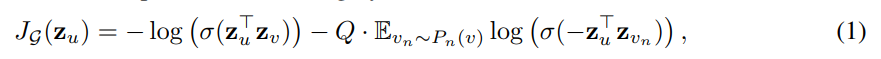
이 loss function은 논문에서 나온 방식을 그대로 이용한다.

neg_score = self.Q*torch.mean(torch.log(torch.sigmoid(-neg_score)), 0)
pos_score = torch.log(torch.sigmoid(pos_score))

neg_score는 일단 max가 아닌 mean을 이용하고 있고, sigmoid에 -neg_score를 넣으므로 실제로 neg_score가 음수이거나 0에 가까울수록 커지고, 양수이고 커질수록 작아지게 된다. 즉 embedding이 차이가 날 수록 점수가 높아진다. 여기에 self.Q = 10을 곱해준다.(Q defines the number of negative samples)
근데 num_negs는 6으로 두고 Q는 10으로 두는 이유는 모르겠다.
또한 pos_score는 min을 하지 않고 전부 이용하고 있다.

nodes_score.append(torch.mean(- pos_score - neg_score).view(1,-1))

이후 -pos_score - neg_score의 합으로 nodes_score를 구하게 되는데, pos_score는 embedding의 차이가 없을수록 점수가 크고, neg_score는 embedding의 차이가 클수록 점수가 크다. 따라서 pos sample과의 차이를 줄이고, neg sample과의 차이를 늘리는 방식으로 훈련이 된다.

elif learn_method == 'plus_unsup':
	# superivsed learning
	logists = classification(embs_batch)
	loss_sup = -torch.sum(logists[range(logists.size(0)), labels_batch], 0)
	loss_sup /= len(nodes_batch)
	# unsuperivsed learning
	if unsup_loss == 'margin':
		loss_net = unsupervised_loss.get_loss_margin(embs_batch, nodes_batch)
	elif unsup_loss == 'normal':
		loss_net = unsupervised_loss.get_loss_sage(embs_batch, nodes_batch)
	loss = loss_sup + loss_net

learn_method가 plus_unsup이라면 GraphSage with Supervised Learning plus Net Unsupervised Learning으로 작동한다.
이는 앞에서 나온 것과 똑같은 방식으로 loss_sup을 구한 후, unsupervised learning 방식으로도 loss_net을 구해 이를 더해 loss를 만드는 방식이다.

이러면 loss도 구했으니 훈련은 거의 끝인데 하나 눈여겨봐야할 점은

loss.backward()
for model in models:
	nn.utils.clip_grad_norm_(model.parameters(), 5)
optimizer.step()

optimizer.zero_grad()
for model in models:
	model.zero_grad()

clipgrad_norm을 통해 gradient clipping을 했다는 점이다. 이를 통해 gradient exploding을 막을 수 있다.

이제 마지막으로 graphSage model을 보면 끝이다. 그 전에 SageLayer를 보면

self.weight = nn.Parameter(torch.FloatTensor(out_size, self.input_size if self.gcn else 2 * self.input_size))

mm 연산에 사용할 weight가 있고,

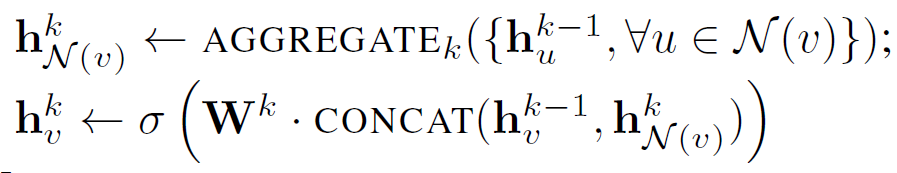
def forward(self, self_feats, aggregate_feats, neighs=None):
	if not self.gcn:
		combined = torch.cat([self_feats, aggregate_feats], dim=1)
	else:
		combined = aggregate_feats
	combined = F.relu(self.weight.mm(combined.t())).t()
	return combined

gcn이 아니라면 self_feats와 aggregate_feats를 concat하여 사용하고, 아니라면 aggregate_feats만 이용한다.
그리고 $W^k \cdot combined$를 계산한 후 activation function(RELU)를 적용한다.

graphSage를 확인해보면

for index in range(1, num_layers+1):
	layer_size = out_size if index != 1 else input_size
	setattr(self, 'sage_layer'+str(index), SageLayer(layer_size, out_size, gcn=self.gcn))

layer를 선언하고,

def forward(self, nodes_batch):
	lower_layer_nodes = list(nodes_batch)
	nodes_batch_layers = [(lower_layer_nodes,)]
	for i in range(self.num_layers):
		lower_samp_neighs, lower_layer_nodes_dict, lower_layer_nodes= self._get_unique_neighs_list(lower_layer_nodes)
		nodes_batch_layers.insert(0, (lower_layer_nodes, lower_samp_neighs, lower_layer_nodes_dict))

nodes_batch를 이용하는데 이 때 nodes_batch는 extend_nodes에서 나온 노드들이다. 즉 원래 배치에서 WALK_LEN만큼 이동하고, N_WALK_LEN보다 멀리 있는 node도 포함되어 있다.

def _get_unique_neighs_list(self, nodes, num_sample=10):
	_set = set
	to_neighs = [self.adj_lists[int(node)] for node in nodes]
	if not num_sample is None:
		_sample = random.sample
		samp_neighs = [_set(_sample(to_neigh, num_sample)) if len(to_neigh) >= num_sample else to_neigh for to_neigh in to_neighs]
	else:
		samp_neighs = to_neighs
	samp_neighs = [samp_neigh | set([nodes[i]]) for i, samp_neigh in enumerate(samp_neighs)]
	_unique_nodes_list = list(set.union(*samp_neighs))
	i = list(range(len(_unique_nodes_list)))
	unique_nodes = dict(list(zip(_unique_nodes_list, i)))
	return samp_neighs, unique_nodes, _unique_nodes_list

node들을 순회해가며 num_sample만큼 neighbor를 샘플링한다.
이 후 sample_neights에 본인 node도 포함시키고, 샘플링한 node들을 중복되지않게 unique하게 하여 _unique_nodes_list를 만든다.
이 후 unique nodes에 index를 매겨 node : index 로 dict를 만들어 unique_nodes로 만든다.
이 후 샘플링된 노드들 samp_neighs, 각 unique한 노드들로 만든 dict인 unique_nodes, unique nodes의 리스트인 _unique_nodes_list를 반환한다.
이 후 nodes_batch의 tuple만 있던 lower_layer_nodes에 (_unique_nodes_list, samp_neighs, unique_nodes) tuple을 list의 맨 앞에 추가한다. 이를 layer의 개수만큼 반복한다.
즉 논문에서 나온 것 처럼 K까지 점점 멀리있는 neighbor를 추가하는데 list의 앞으로 갈 수록 node의 개수가 많아진다는 것이다.

pre_hidden_embs = self.raw_features
for index in range(1, self.num_layers+1):
	nb = nodes_batch_layers[index][0]
	pre_neighs = nodes_batch_layers[index-1]
	# self.dc.logger.info('aggregate_feats.')
	aggregate_feats = self.aggregate(nb, pre_hidden_embs, pre_neighs)
	sage_layer = getattr(self, 'sage_layer'+str(index))
	if index > 1:
		nb = self._nodes_map(nb, pre_hidden_embs, pre_neighs)
	# self.dc.logger.info('sage_layer.')
	cur_hidden_embs = sage_layer(self_feats=pre_hidden_embs[nb],
								aggregate_feats=aggregate_feats)
	pre_hidden_embs = cur_hidden_embs

return pre_hidden_embs

이 후 num_layers만큼 loop를 하는데,
첫loop에서 nb는 첫번째 neighbor까지 추가했을 때, _unique_nodes_list이고, pre_neighs는 neighbor을 추가하지 않은 nodes_batch이다.
pre_hidden_embs = self.raw_features = 전체 node의 features이다.

def aggregate(self, nodes, pre_hidden_embs, pre_neighs, num_sample=10):
	unique_nodes_list, samp_neighs, unique_nodes = pre_neighs

	# len(nodes) = m
	# len(samp_neighs) = m
	# len(unique_nodes_list) = n
	# len(unique_nodes) = n
	# len(pre_hidden_embs) = n
	# 이라고 한다. m <= n
	# m개의 node에서 n개의 neighbor를 뽑아내고, 그 neighbor에 해당하는 hidden_embs를 뽑아내는 것이다.
	assert len(nodes) == len(samp_neighs)
	indicator = [(nodes[i] in samp_neighs[i]) for i in range(len(samp_neighs))]
	assert (False not in indicator)
	if not self.gcn:
		samp_neighs = [(samp_neighs[i]-set([nodes[i]])) for i in range(len(samp_neighs))]
	if len(pre_hidden_embs) == len(unique_nodes):
		embed_matrix = pre_hidden_embs	# n x d
	else:
		embed_matrix = pre_hidden_embs[torch.LongTensor(unique_nodes_list)]
	mask = torch.zeros(len(samp_neighs), len(unique_nodes))	# m x n
	column_indices = [unique_nodes[n] for samp_neigh in samp_neighs for n in samp_neigh]	# sampling size * m 이하의 크기를 가진다.
	row_indices = [i for i in range(len(samp_neighs)) for j in range(len(samp_neighs[i]))]	# sampling size * m 이하의 크기를 가진다.
	mask[row_indices, column_indices] = 1	# adj 느낌으로 mask를 만든다.

	if self.agg_func == 'MEAN':
		num_neigh = mask.sum(1, keepdim=True)
		mask = mask.div(num_neigh).to(embed_matrix.device)
		aggregate_feats = mask.mm(embed_matrix)	# [m x n] x [n x d] = [m x d]

	elif self.agg_func == 'MAX':
		# print(mask)
		indexs = [x.nonzero() for x in mask==1]
		aggregate_feats = []
		for feat in [embed_matrix[x.squeeze()] for x in indexs]:
			if len(feat.size()) == 1:
				aggregate_feats.append(feat.view(1, -1))
			else:
				aggregate_feats.append(torch.max(feat,0)[0].view(1, -1))
		aggregate_feats = torch.cat(aggregate_feats, 0)
	
	return aggregate_feats

이를 self.aggregate로 aggregate_feats로 만들어 주는데, aggregate func는 논문에서는 gcn, mean, lstm, pool을 이용했지만, 이 구현에서는 기본이 mean이고 이외에 pool를 구현했다. pool과 lstm의 성능이 가장 좋다고 했는데 lstm은 속도도 느리고 pool과 성능이 비슷하므로 넣지 않은 것 같다.
aggregate는 코드를 보고 차원을 계산하면서 천천히 이해하면 될 것이다.

이후엔 pre_neighs의 node to index dict를 이용해 현재 node인 nb를 index로 변환하고(pre_neighs의 노드가 현재 node들을 포함하는 형태이므로 가능하다)
sage에 이전의 hidden_emb를 현재 nb를 index로 얻어(m x d) self_feats로 하고, aggregate에서 나온 hidden emb(m x d)를 aggregate_feats로 한다.
결과 갚은 m x d가 된다.
결국 layer를 반복하면 num_batch x d의 embedding이 결과로 나오게 된다.
이 결과로 위에서 설명한 apply_model을 끝까지 진행하면 된다.