📌 확률변수란?
변수는 말그대로 "변하는 수"를 말하죠. 그렇다면 확률변수는 무엇을 일까요? 확률변수란 영어로 random variable로 무작위로 시험했을 때 각 경우의 결과를 수치적으로 나타낸 변수를 의미합니다.
사전적 정의로 이해하기 어려우니 예시를 들어 설명해보도록 할께요!
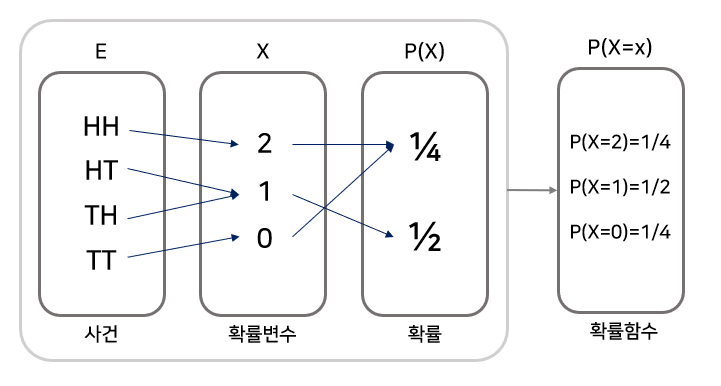
동전을 두번 던졌을 때 발생되는 경우는 HH,HT,TH,TT로 4가지 입니다. "앞면이 몇번 나올 것인가"에 대해 실수값을 대응시키는 작업을 "확률 변수"만드는 과정이라고 합니다.
- 확률변수 (즉, 앞면의 갯수)가 2인경우: HH (1개)
- 확률변수 (즉, 앞면의 갯수)가 1인경우: TH, HT (2개)
- 확률변수 (즉, 앞면의 갯수)가 0인경우: TT (1개)
- 확률변수가 2가 될 확률: 1/4
- 확률변수가 2가 될 확률: 2/4
- 확률변수가 2가 될 확률: 1/4
📌 확률변수 종류
확률변수는 이산 확률변수(discrete random variable)과 연속 확률변수(continuous random variable)로 구분할 수 있습니다. 확률 변수를 이산 확률 변수와 연속 확률 변수로 구분하는 기준은 그 값이 가능한 결과의 집합이나 범위의 특성에 따라 결정됩니다.
간단히 말하면 결과값을 셀수 있으면 이산확률변수 셀수 없는 경우를 연속확률변수라고 할 수 있습니다.
1️⃣ 이산확률변수 (discrete random variable)
- 이산확률변수의 특징
- 이산 확률 변수는 유한한 또는 세기 가능한 값을 가집니다. 즉, 값의 개수가 셀 수 있거나 유한합니다.
- 표, 함수, 그래프로 나타낼 수 있습니다.
- 이산 확률 변수는 각각의 값에 대한 확률을 정의할 수 있습니다. 따라서 이산 확률 변수의 확률 분포는 확률 질량 함수를 사용하여 나타낼 수 있습니다. (🤭 질량 함수에 대해 밑에서 자세히 설명할께요!)
- 이산확률변수의 예시
- 어느 날 동물원의 입장갯수
- 2개의 동전을 던졌을 때 나올 수 있는 앞면 갯수
- 스트라이크를 성공할 때 가지 볼링공을 굴린 횟수
2️⃣ 연속확률변수 (continuous random variable)
- 이산확률변수의 특징
- 연속 확률 변수는 실수 범위 내에서 무한한 가능한 값을 가집니다. 즉, 값의 개수가 무한히 많을 수 있습니다.
- 연속 확률 변수는 각각의 특정 값에 대한 확률을 정의할 수 없으며, 대신 구간(interval) 내의 확률을 정의합니다. 이를 위해 확률 밀도 함수를 사용합니다.(🤭 밀도 함수에 대해 밑에서 자세히 설명할께요!)
- 표로는 나타낼 수 없지만, 함수와 그래프로 나타낼 수 있습니다.
- 시간,온도,길이,무게 등은 무한개의 연속적 값을 가지므로 연속확률변수에 속할 수 있습니다.
- 연속확률변수의 특징
- 어느 지역에 일년 동안 내리는 강수량
- 어느 공장에서 생산된 전구의 수명
- 한 버스가 오기까지의 시간
📌 확률분포
이산확률변수는 질량 함수으로 나타내고 연속확률변수는 밀도함수로 나타낼수 있다고 앞서 말씀드렸는데요.이에 대해 더 자세히 설명하려고 합니다. 이를 위해 확률 분포가 뭔지 먼저 짚고 넘어가도록 하겠습니다. 확률 분포는 어떤 사건의 가능한 결과들과 그 결과들이 일어날 확률을 보여주는 것입니다.
예를 들어 주사위를 던져서 어떤 숫자가 나올지 생각해봅시다. 각 숫자가 나올 확률은 같아서 1/6이 될 것입니다. 이렇게 가능한 결과와 그 결과들이 일어날 확률을 모아놓은 것이 확률 분포입니다. 이 또한 확률변수와 같이 "이산확률분포"과 "연속확률분포"로 나뉩니다.
1️⃣ 이산확률분포
이산확률변수에서 말한 예시를 들자면 주사위를 던져 나온 숫자를 생각해봅시다. 이 주사위는 5면으로 이루어져 있으며 각 숫자의 면의 넓이 다릅니다. 이러한 주사위를 던졌을때 각 숫자가 나올 확률이 아래와 같다고 가정해봅시다!
- 1이 나올 확률: 2/15
- 2가 나올 확률: 3/15
- 3이 나올 확률: 5/15
- 4이 나올 확률: 3/15
- 5이 나올 확률: 2/15
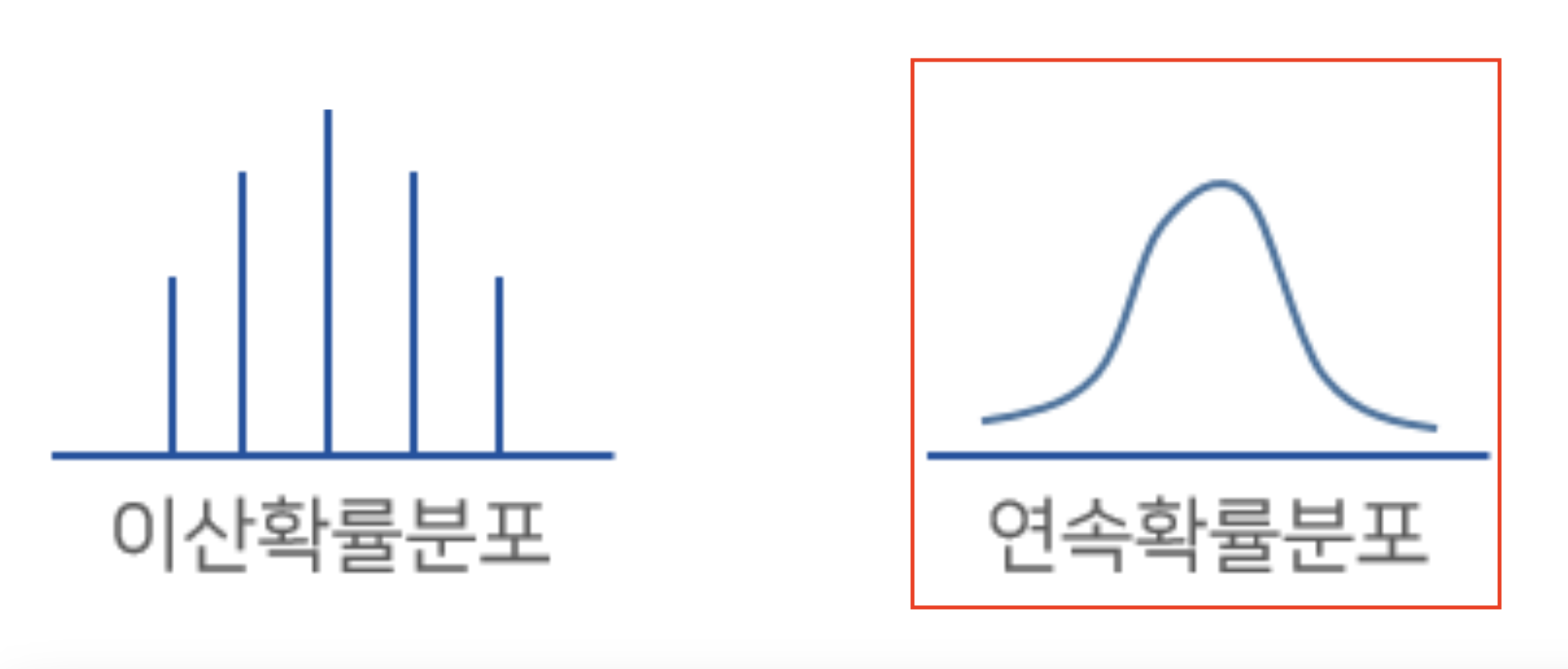
각 숫자를 x에 두고 x일때 나올수 있는 확률을 y로 하여 그래프를 그린다면 아래 이미지의 왼쪽과 같을겁니다.
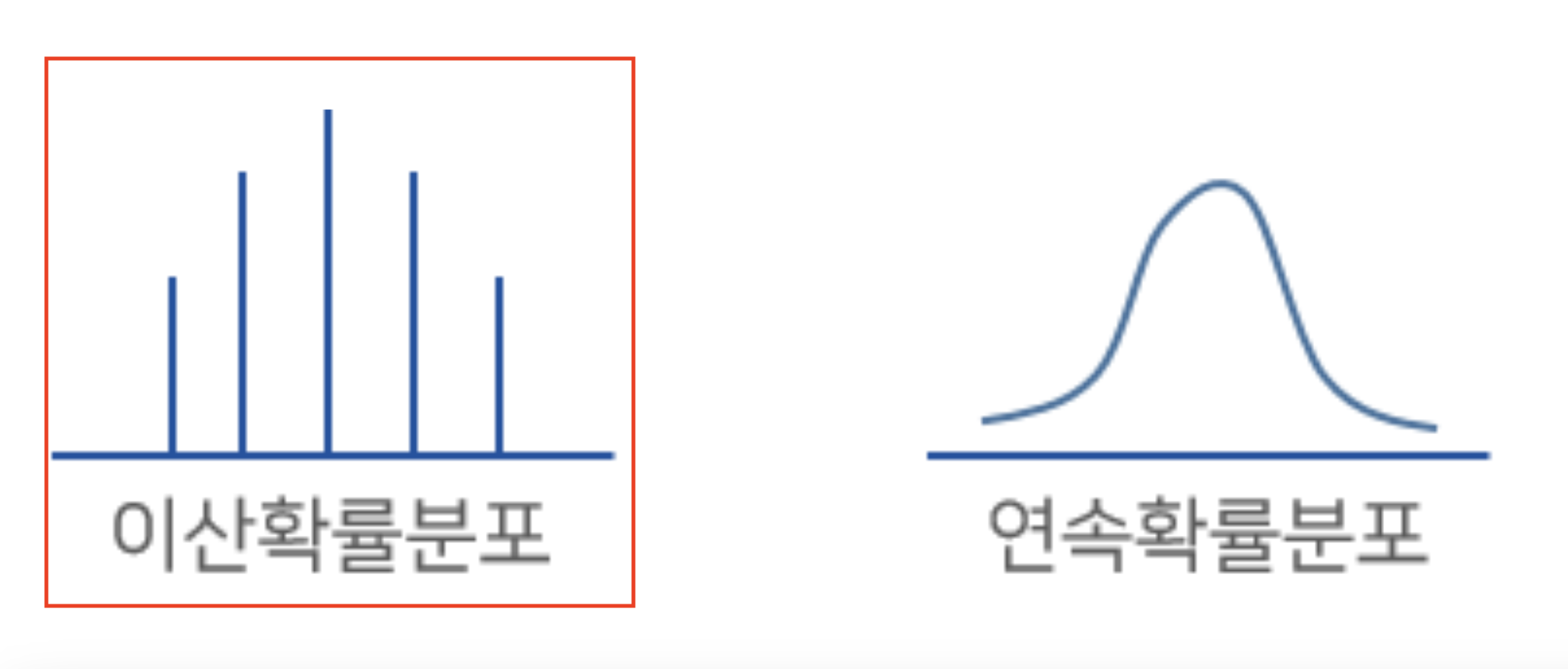
만약 숫자3이 나올 확률을 묻는다면 x가 3일때 y값을 구하면 됩니다. 이와 같이 이산 확률 분포에서 특정 값 x에 대한 확률을 나타내는 함수를 확률 질량 함수(probability mass function, PMF)라고 합니다. 확률 질량 함수로 이산 확률 분포를 나타낼 수 있습니다.
2️⃣ 이산확률분포
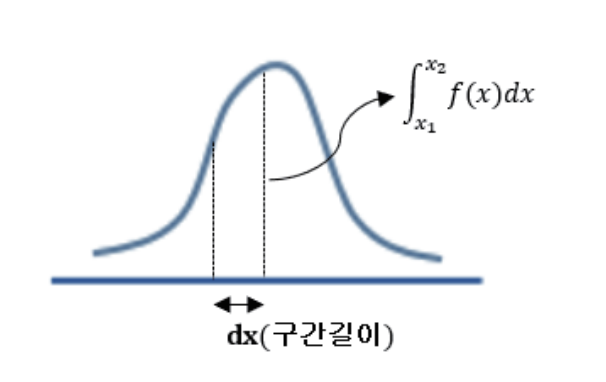
이산확률분포는 주사위 예시처럼 딱딱 나눠진 값이 아니라 어떤 범위 내에서 일어날 수 있는 경우입니다. 예를 들어, 온도나 시간과 같은 것들이 연속 확률 분포를 가집니다. 예를 들어 24시간동안 기온 변화를 나타내는 그래프가 있다고 생각해봅시다. (x축이 시간 y축이 온도입니다) 시간이란 무한한 가능한 값(1시 1분 1초, 1시 1.111111초 ...)들의 범위에서 값을 가지므로 선으로 된 그래프를 만들게 될겁니다.
시간개념은 연속적인 개념이기에 특정 값 하나에 대한 확률을 직접 계산하기 어렵습니다. 따라서 우리가 알고 싶은 사건이 발생하는 구간의 넓이를 계산함으로써 그 사건이 발생할 확률을 계산할 수 있습니다. 이를 확률 밀도 함수(probability density function, PDF))라고 합니다