ML/DL을 위한 필수 확률과 통계 개념 익히기 📈
1.[확률/통계] 확통 단어 개념 정리하기: 모집단, 표본

확률과 통계(aka. 확통)기초 공부를 시작하기 전에 몇가지 중요 개념을 반드시 이해하고 넘어간다면 조금 수월합니다. 무턱대고 외웠더니 나중에 개념들이 꼬여 다시 기초부터 배워야 하는 순간이 찾아옵니다.... 🥲(그게 바로 나..;;)그래서 확률/통계 시리즈를 찬찬히
2.[확률/통계] 확률변수(random variable)
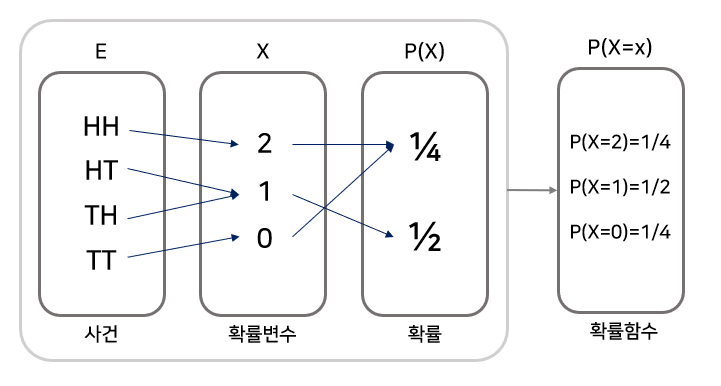
변수는 말그대로 "변하는 수"를 말하죠. 그렇다면 확률변수는 무엇을 일까요? 확률변수란 영어로 random variable로 무작위로 시험했을 때 각 경우의 결과를 수치적으로 나타낸 변수를 의미합니다. 사전적 정의로 이해하기 어려우니 예시를 들어 설명해보도록 할께요!
3.[확률/통계] 헷갈리는 확률분포 개념잡기- 베르누이, 이항, 포아송

개념어떤 일을 1번 시행할때 일어날 확률 p, 일어나질 않을 확률 q라고 정의함 하지만 이때, 시행마다 일어날 확률은 항상 일정해야 함 표현 B(n,p) = B(시행횟수, 성공할 확률) 공식 이항분포의 기댓값 $E(X) = np$이항분포의 분포$V(X) = npq$이
4.이산확률분포 - 정규분포
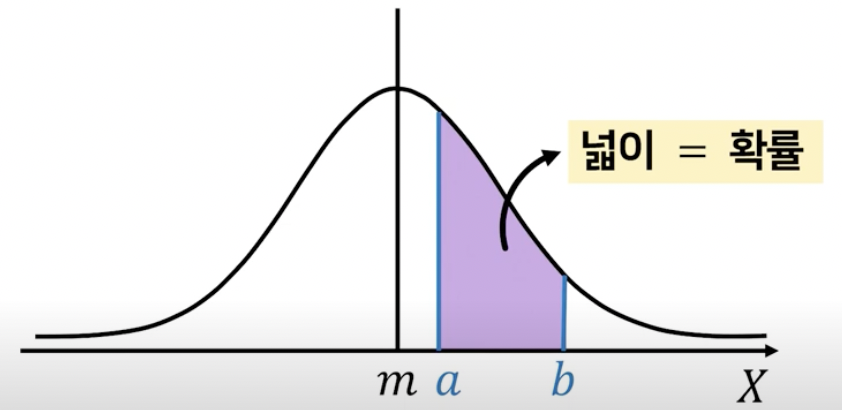
표현 N(m,\\sigma ^2) = N(평균, 분산) 확률변수 X가 정규 분포 $N(30, 4^2)$을 따를 때, 다음 표준정규분포표을 이용하여 $P(22 \\leq X \\leq 42)$를 구하시오.문제풀이x축 22부터 42까지의 색칠된 넓이를 구하면 이는 확률을
5.[확률/통계] 베이즈 정리(Bayess' Theorm)

베이즈 정리를 사용하는 이유구하기 어려운 확률을 쉬운 확률을 사용하여 구하기 위함베이즈 정리 공식$P(A|B) = \\frac{P(B|A)\\times P(A)}{P(B)}$$P(A|B) = \\frac{P(B|A)\\times P(A)}{P(B|A)P(A)+P(B|A
6.이산확률변수 기댓값(평균)

확률변수 기댓값 공식$\\mu = E(X) = \\sum\_{x_i} x_iP(X=x_i)$확률변수 기댓값 예시기대값 공식에 수치를 대입해 보자! $\\mu = E(X) = \\sum\_{x_i} x_iP(X=x_i)$ $=x_1P(X=x_1)+x_2P(X=x_2)
7.이산확률변수 분산 및 표준편차

확률변수 산포도 공식 \-$\\sigma^2 = Var(X) = E((X-\\mu)^2)$= $E(X^2) -|E(x)|^2$ 확률변수 표준편차 $\\sigma = \\sqrt Var(X)$ 평균으로부터 결과값이 얼마나 다른지 나타내는 것은같으나, 확률변수와 같은