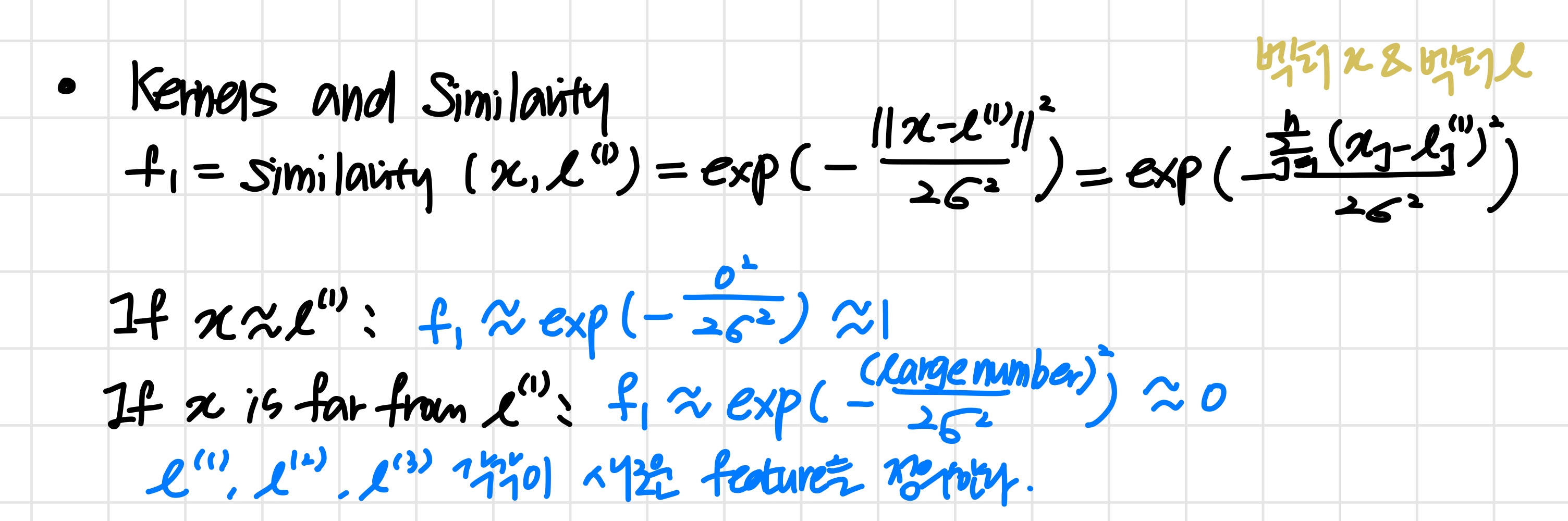[ML] 7주차-2 : Kernels

Machine Learning by professor Andrew Ng in Coursera

1) Kernels I

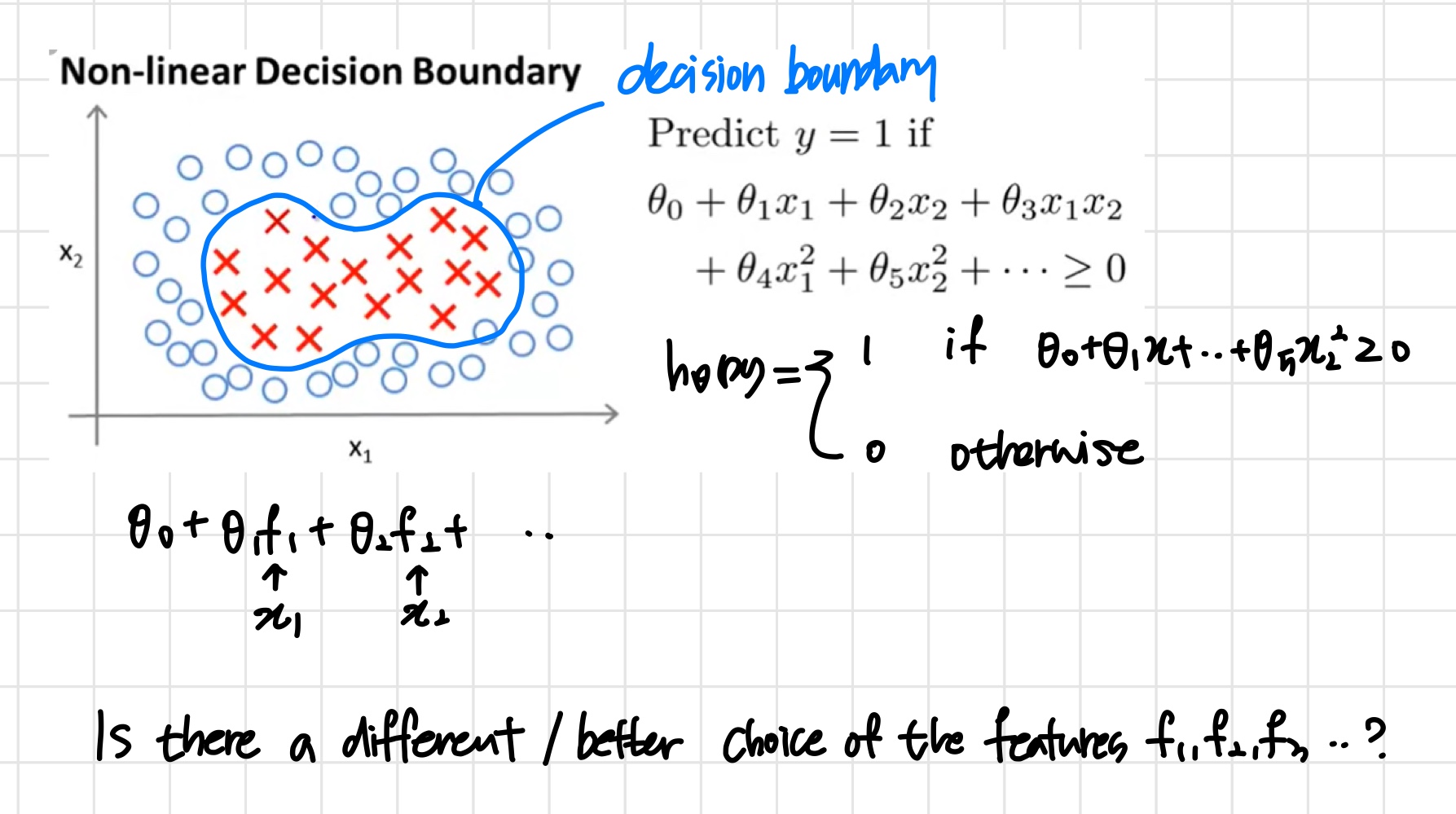
위와 같은 data에는 non-linear decision boundary가 필요하다.
이때 svm classifier의 목표는
$\theta_0 + \theta_1x_1 + \theta_2x_2+ ... + \geq 0$일 때 $y = 1$로 예측해 내는 것이다.
이때 $x_1, x_2, x_1^2..$ 등 feature들의 자리를 $f_1, f_2, f_3..$등 좀 더 일반화된 형태로 다시 고쳐본다.
이때 $f_1, f_2, f_3..$들은 기존의 feature들, $x_1, x_2, x_1^2..$이 어떤 과정을 거쳐 변환된 새로운 feature들이다.
이 $f_1, f_2, f_3..$를 구하는 과정에 대해 알아본다.

Kernel

---

• feature space에 임의의 landmark $l^{(1)}, l^{(2)}, l^{(3)}$이 있다고 가정한다.
• 새로운 feature $f_1, f_2, f_3..$ 들은 이 landmark들과 기존의 $x_1, x_2, x_1^2..$들 간의 거리로 결정된다.
• 이때 Gaussian 함수를 이용한다.

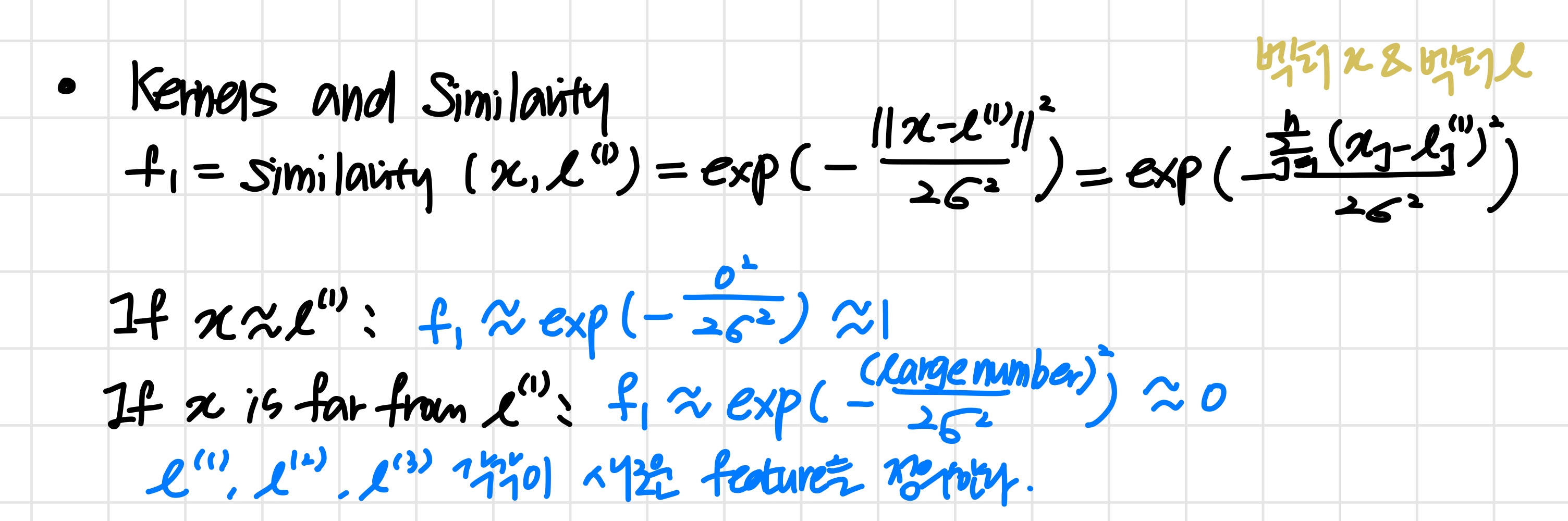
• $x$가 $landmark$와 가깝다면 해당 $f_i \approx 1$이 되고, 그렇지 않다면 $f_i \approx 0$이 된다.

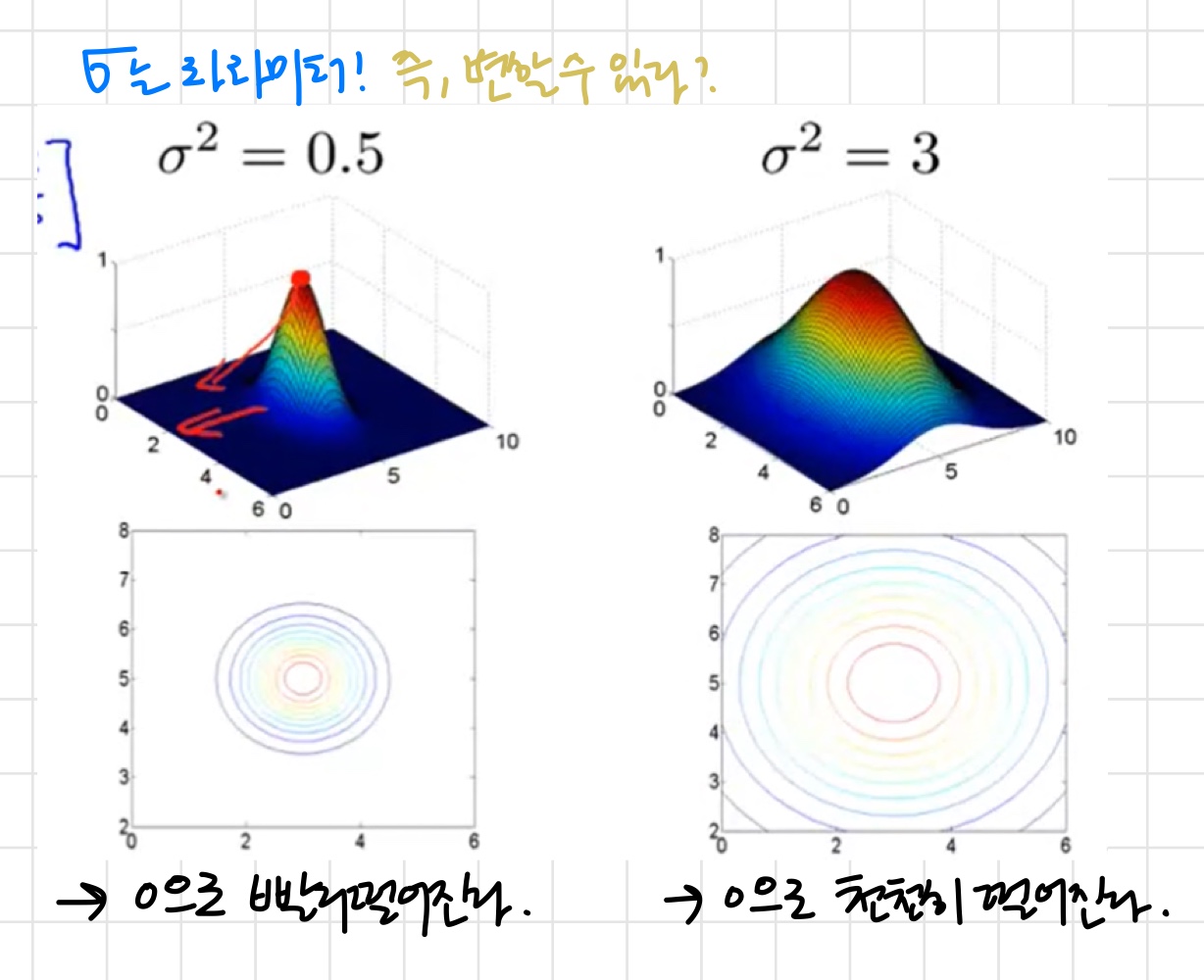
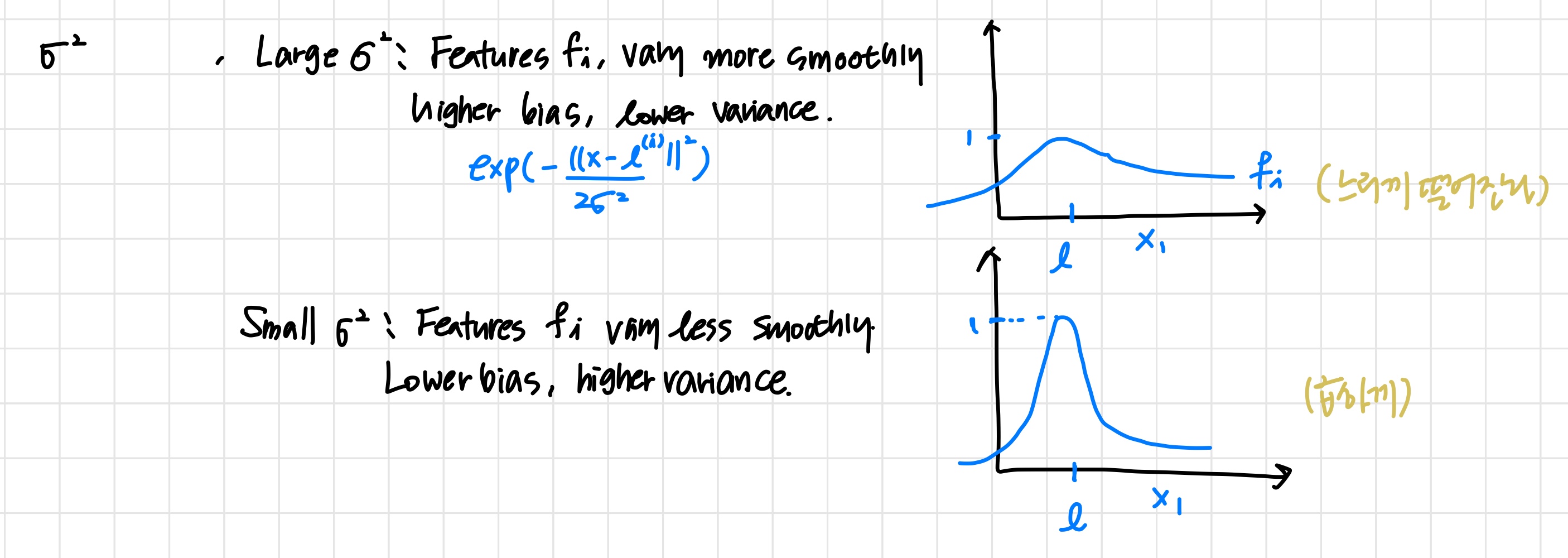
• 파라미터 $\sigma$
  '값이 변할 수 있기 때문에 이거에 따른 변화 ~..'

• $\color{pink}x$가 $l^{(1)}$과 가깝기 때문에 $f_1 \approx1, f_2 \approx0, f_3 \approx0$.
  $\theta_0 + \theta_1\times1 + \theta_2\times0 + \theta_3\times0 = -0.5 + 1 \geq 0$ 이므로
  $y=1$로 예측
• $\color{green}x$가 $l^{(1)}$과 가깝기 때문에 $f_1 \approx1, f_2 \approx0, f_3 \approx0$.
  $\theta_0 + \theta_1\times1 + \theta_2\times0 + \theta_3\times0 = -0.5 + 1 \geq 0$ 이므로
  $y=1$로 예측
• 이런 식으로 여러 $x$들을 각 landmark와 비교해 보고 $y$를 예측해 나가면서 decision boundary를 구할 수 있다.

2) Kernels II

'기존 feature $x$들과 landmark간의 거리를 이용해서 새로운 feature $f_i$를 만들어냈다. 그럼 이 landmark들은 어떻게 생겨났는지에 대해 알아본다.'

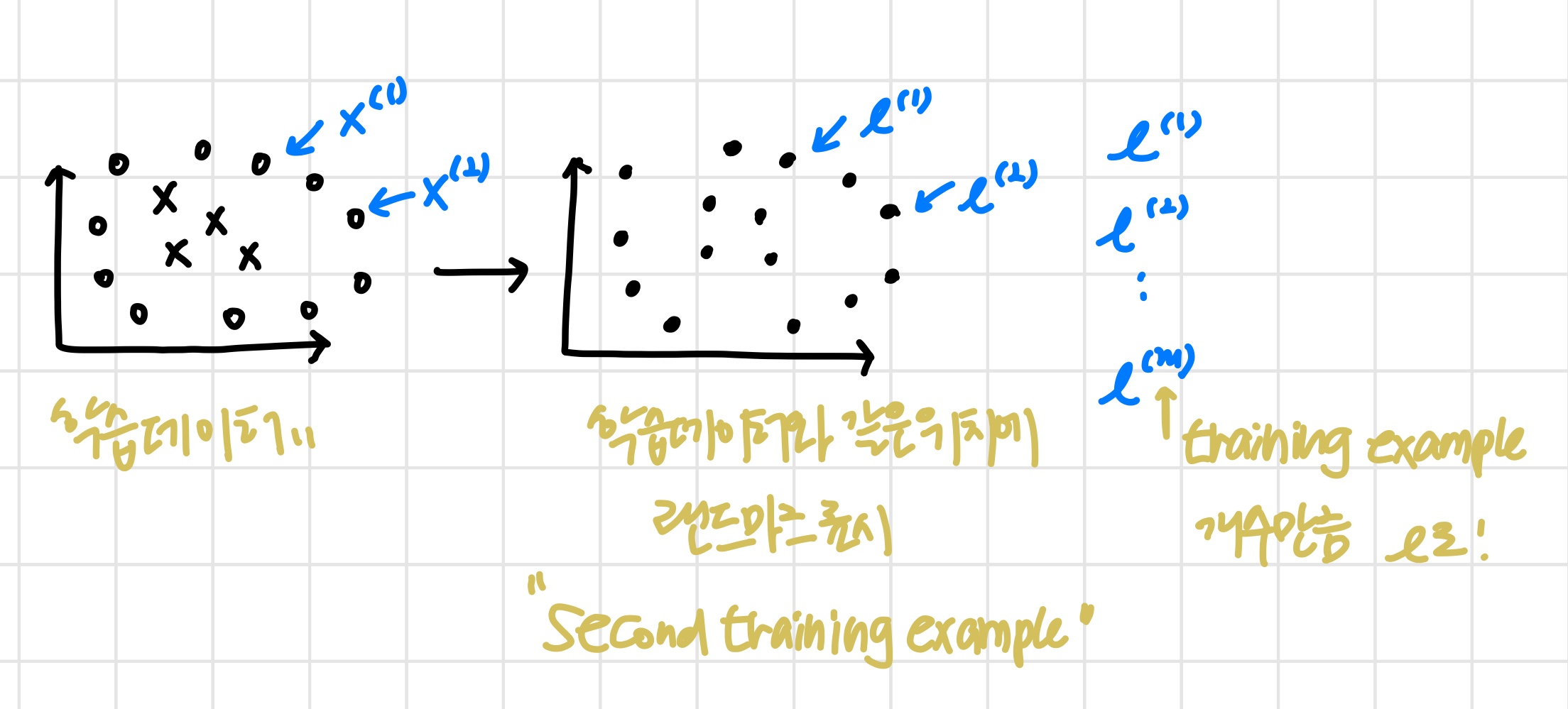
• 한 가지 방법은 학습데이터와 같은 위치에 랜드마크를 표시하는 것

SVM with Kernels

---

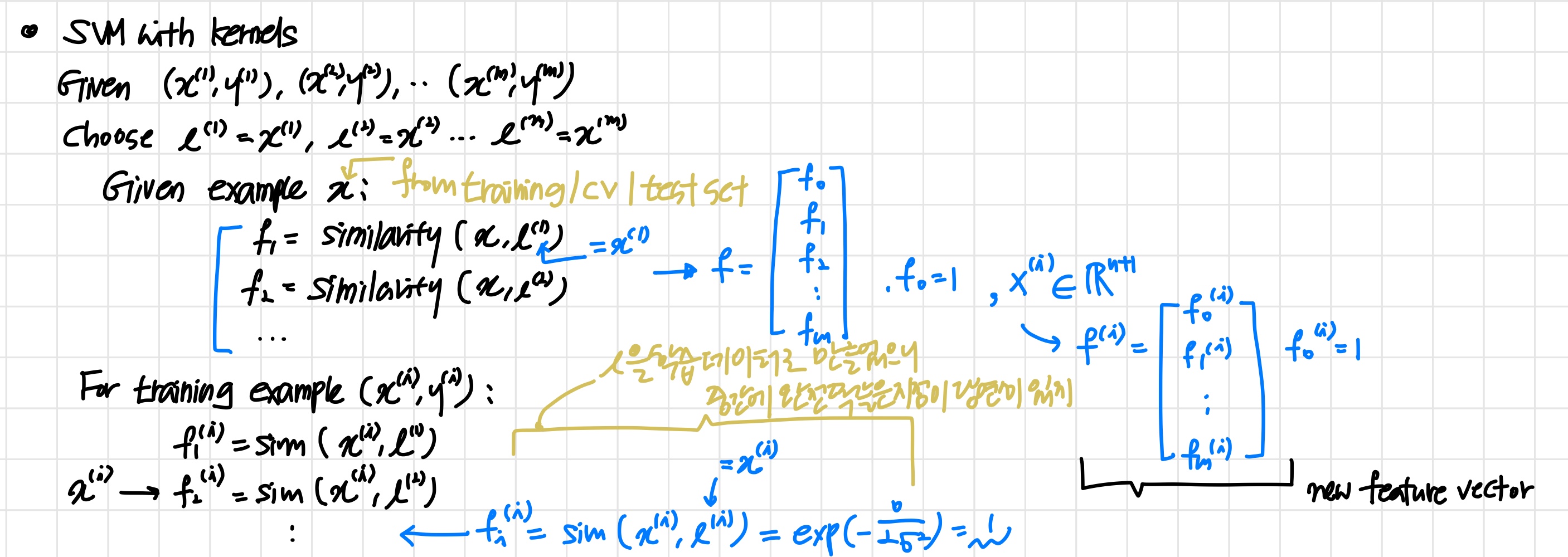
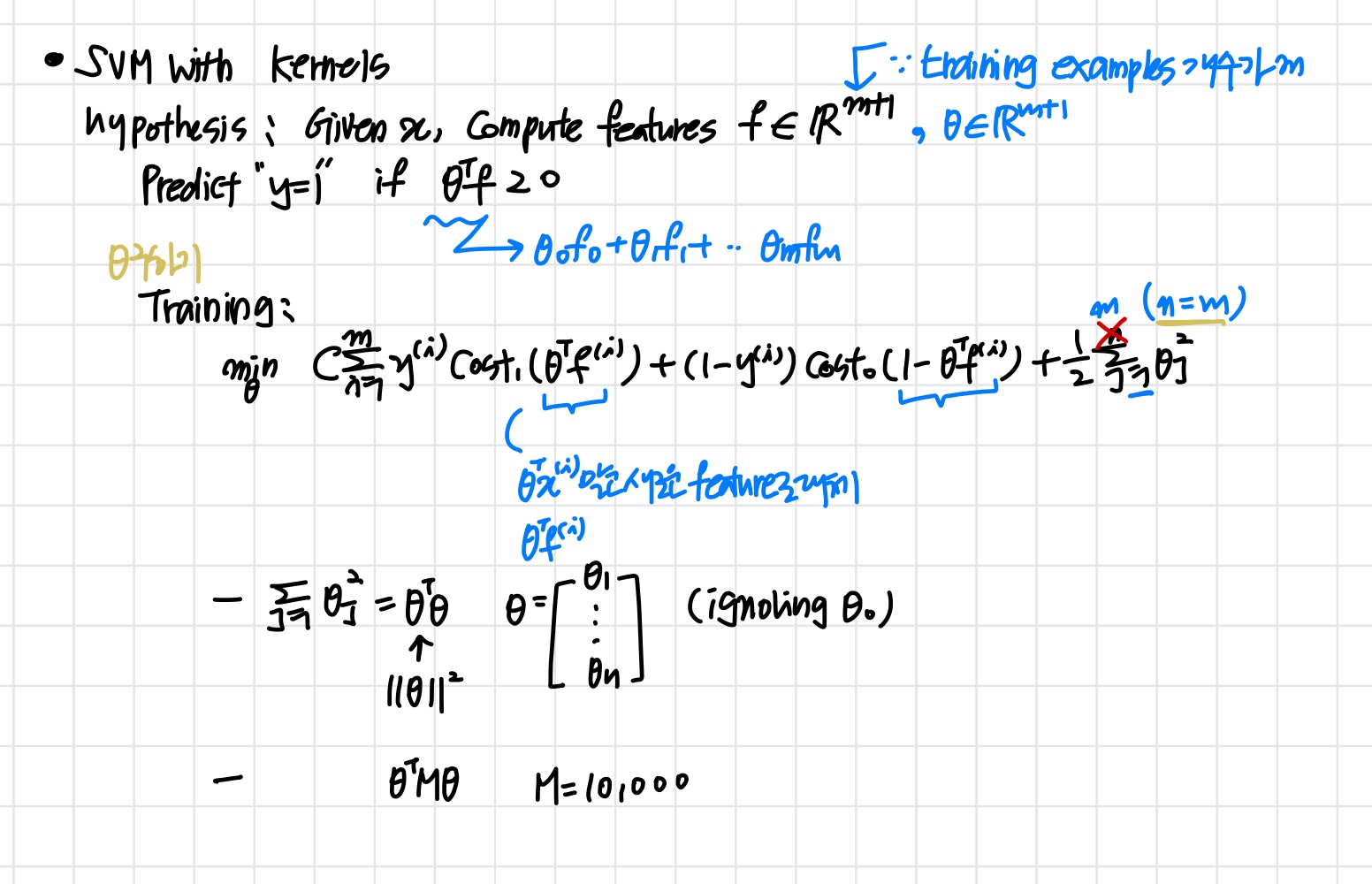
SVM이 아닌 다른 알고리즘에도 kernel 개념을 적용할 순 있지만 연산속도가 매우 느려진다.

SVM parameters

---