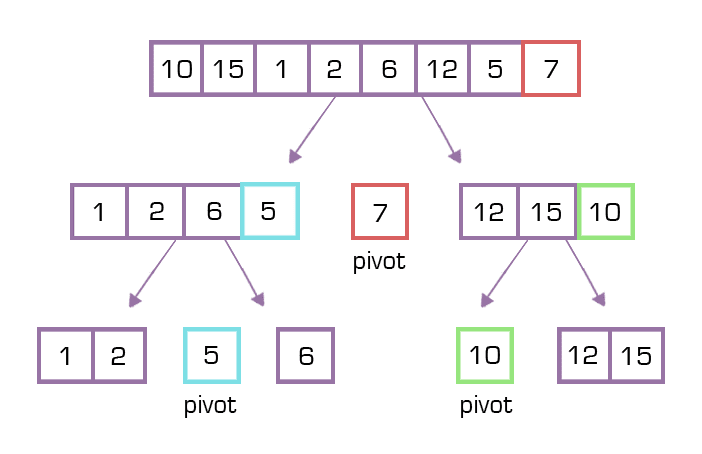
퀵 정렬에서는 먼저 기준점(Pivot)을 하나 정하고, pivot보다 작으면 left 배열에, pivot보다 크면 right 배열에 삽입합니다. 이때, pivot은 첫번째 데이터로 정하면 됩니다. 그 다음으로는 left와 right 배열에 대해서도 똑같이 각각 pivot을 정하고 pivot의 값을 기준으로 left와 right로 값들을 모읍니다. 결국 left와 right의 크기가 1이 될때까지 합니다. 마지막으로, left+pivot+right 을 리턴함으로써 최종적으로 정렬된 데이터를 반환합니다.

Pseudo Code

파이썬(Python)

def quickSort(data):
    if len(data) <= 1:
        return data
    
    pivot = data[0]
    left = []
    right = []
    
    for d in data:
        if d < pivot:
            left.append(d)
        elif d > pivot:
            right.append(d)
        else:
            continue
    
    return quickSort(left) + [pivot] + quickSort(right)
    

자바(Java)

public class QuickSort {

    public List<Integer> quick_sort(List<Integer> data) {
        if (data.size() <= 1) {
            return data;
        }

        int pivot = data.get(0);

        List<Integer> left = new ArrayList<>();
        List<Integer> right = new ArrayList<>();

        List<Integer> sorted_list = new ArrayList<>();

        data.forEach(d -> {
            if (d < pivot) {
                left.add(d);
            } else if (d > pivot) {
                right.add(d);
            } else {
                return;
            }
        });

        sorted_list.addAll(quick_sort(left));
        sorted_list.add(pivot);
        sorted_list.addAll(quick_sort(right));

        return sorted_list;
    }
}

시간복잡도

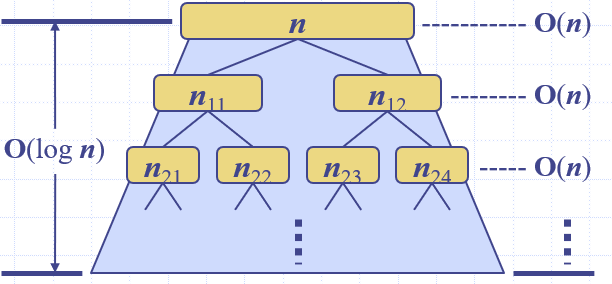
평군 시간복잡도는 O(n log n) 입니다. 왜냐하면, n개의 데이터를 결국 이진 트리처럼 나누게 되며, n개의 데이터에 대해서 높이가 h 일때, h = $log n$인데, 각 높이/깊이마다 n개의 데이터가 있고, n개의 데이터 모두 비교를 하기 떄문에 각 높이/깊이에서 O(n)의 시간이 걸립니다. log n의 높이에 대해서 O(n)의 시간이 걸리므로, 시간복잡도는 O(n $logn$)이 됩니다.

하지만, 최악의 경우에는 O($n^2$)이 됩니다. 왜냐하면, 만약에 각 높이에서 pivot이 나머지 모든 값들보다 크거나 작으면, 결국 left 또는 right 한쪽으로만 n-1개의 데이터가 쌓이게 됩니다. 그러면 결국 트리의 높이는 n이 됩니다. 높이 n에 대해서 n번의 비교가 이루어지므로, O($n^2$)이 됩니다.