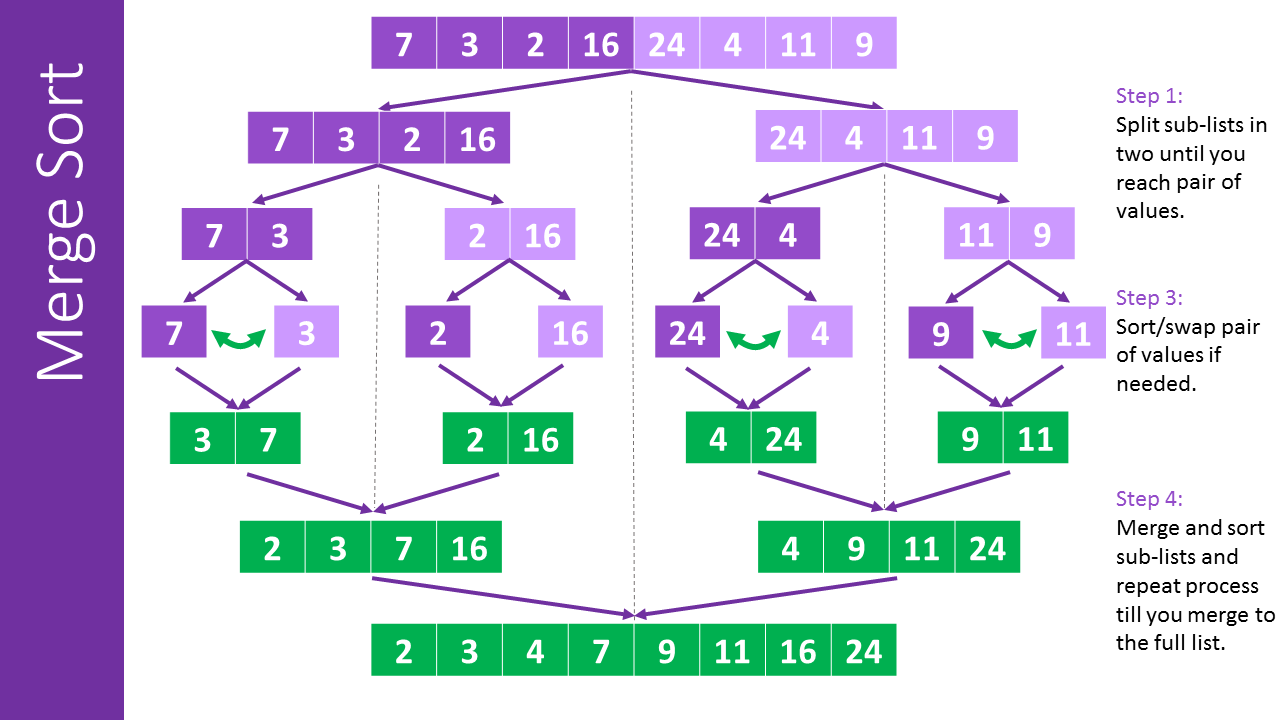
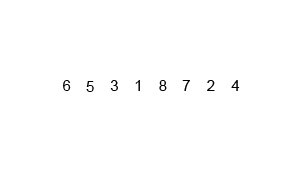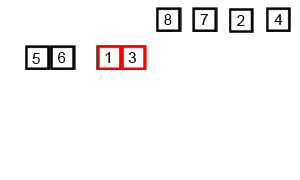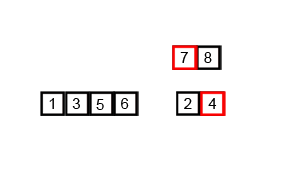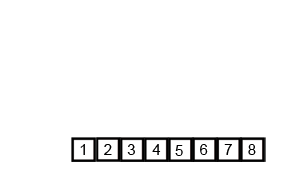합병 정렬은 분할 통치법(Divide and Conquer) 알고리즘을 이용한 대표적인 정렬 방법입니다. 분한 통치법은 문제를 나눌 수 없을 때까지 나눈 후, 다시 합병함으로써 문제를 푸는 방법입니다. 하양식 접근 법으로, 상위의 값을 구하기 위해, 아래로 내려가면서 답을 구합니다. 대표적으로 퀵 정렬과 합볍 정렬이 있습니다.

합병 정렬은 우선 리스트에 하나의 값만 남을때까지 반으로 쪼갭니다. 쪼갠 후, 각 리스트의 첫번째째 원서를 서로 비교해서, 더 작은 값을 새로운 리스트에 추가하면서 쪼갠 리스트들을 합병하는 과정을 거칩니다. 결국, 정렬된 리스트가 완성이 됩니다.

Pseudo Code

파이썬(Python)

def merge(left, right):
    lp = 0
    rp = 0
    sorted_list = []
    
    # left랑 righr에 둘 다 정렬이 되지 않았을때
    while lp < len(left) and rp < len(right):
        if left[lp] < right[rp]:
            sorted_list.append(left[lp])
            lp = lp + 1
            continue
        elif left[lp] > right[rp]:
            sorted_list.append(right[rp])
            rp = rp + 1
            
    # right의 데이터는 모두 정렬이 됐는데 left에는 정렬되지 않은 데이터가 있을때
    if lp < len(left) and rp >= len(right):
        while lp < len(left):
            sorted_list.append(left[lp])
            lp = lp + 1
            
    # left의 데이터는 모두 정렬이 됐는데 right에는 정렬되지 않은 데이터가 있을때
    if lp >= len(left) and rp < len(right):
        while rp < len(right):
            sorted_list.append(right[rp])
            rp = rp + 1
    
    #print(sorted_list)
    return sorted_list

def split_list(data):
    if len(data)<= 1:
        return data
    partition = int(len(data)/2)
    left = split_list(list(data[0:partition]))
    right = split_list(list(data[partition:]))
    
    return merge(left, right)
    

자바(Java)

public class MergeSort {

    public List<Integer> merge_sort(Integer[] data) {
        List<Integer> data_list = List.of(data);

        return splitAndMergeList(data_list);
    }

    private List<Integer> splitAndMergeList(List<Integer> data_list) {
        int size = data_list.size();

        if (size <= 1) {
            return data_list;
        }

        int partition = size / 2;
        List<Integer> left = new ArrayList<>();
        List<Integer> right = new ArrayList<>();
        for (int i = 0; i < size; i++) {
            if (i < partition) {
                left.add(data_list.get(i));
            } else {
                right.add(data_list.get(i));
            }
        }

        return merge_lists(splitAndMergeList(left), splitAndMergeList(right));
    }

    private List<Integer> merge_lists(List<Integer> left, List<Integer> right) {
        List<Integer> sorted_list = new ArrayList<>();
        int lp = 0;
        int rp = 0;
        int lSize = left.size();
        int rSize = right.size();

        while (lp < lSize && rp < rSize) {
            if (left.get(lp) < right.get(rp)) {
                sorted_list.add(left.get(lp++));
            } else {
                sorted_list.add(right.get(rp++));
            }
        }

        while (lp < lSize) {
            sorted_list.add(left.get(lp++));
        }
        while (rp < rSize) {
            sorted_list.add(right.get(rp++));
        }

        return sorted_list;
    }

}

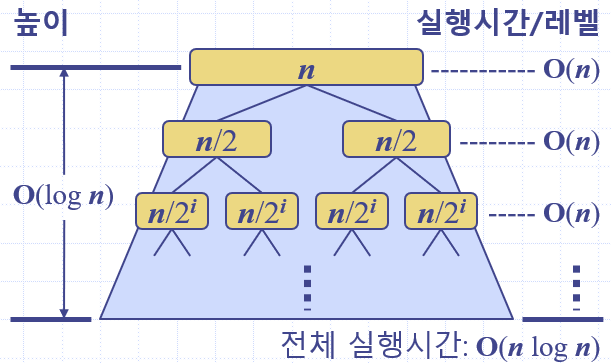
시간 복잡도

리스트를 쪼개는 과정에서, 무조건 각 리스트를 반으로 쪼개기 때문에, 데이터 n개에 대해서 높이가 $logn$인 이진 트리가 생성이 됩니다. 이때, 각 단계에서 n개의 데이터를 비교하기 때문에, 각 단계에서 걸리는 시간은 O(n) 입니다. 그렇기 때문에 시간 복잡도는 O(n) * O($logn$) 으로써, O(n $logn$)이 됩니다.