트리?
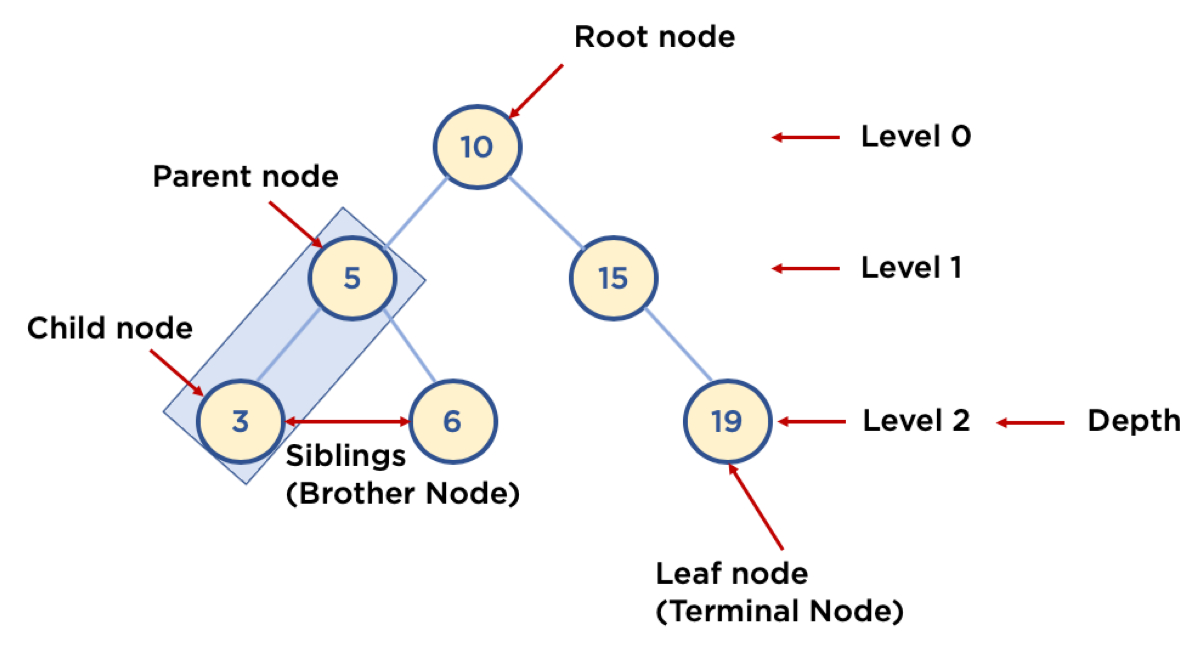
값을 저장하고 있는 노드(Node)들이 Branch로 연결되어 있는 데이터 구조입니다. 가장 위에 있는 루트 노드(Root Node)에서 시작해서 밑으로 갈 수록 연결되어 있는 노드들이 많아지면서, 거꾸로 봤을때 나무 같기 때문에 트리라고 부릅니다.
(http://www.fun-coding.org/00_Images/tree.png)
용어:
- Node: 트리에서 데이터를 저장하는 기본 요소
- Root Node 또는 Root: 트리에서 가장 위에 있는 노드 (탐색의 시작점)
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node(부모 노드): 어떤 노드의 바로 위에 연결된 노드
- Child Node(자식 노드): 어떤 노드의 바로 하위에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
이진 탐색 트리(Binary Search Tree)
(https://www.mathwarehouse.com/programming/images/binary-search-tree/binary-search-tree-insertion-animation.gif)
하나의 부모 노드에 대해서 가질 수 있는 최대의 자식 노드가 2개로 이루어진 트리입니다. 이진 탐색 트리에서 무조건 지켜야되는 규칙으로는 부모 노드보다 값이 작은 자식 노드는 왼쪽 자식 노드, 부모 노드보다 값이 큰 노드는 오른쪽 자식 노드로 저장해야 된다는 것 입니다.
노드 추가하기
def insert(self, value):
node = self.root
while True:
if node.value <= value:
if node.right == None:
node.right = Node(value)
return
else:
node = node.right
else:
if node.left == None:
node.left = Node(value)
return
else:
node = node.left노드를 추가하기 위해서는 노드가 저장되어야 하는 위치를 찾아줘야합니다. 루트 노드로 시작해서 Leaf Node가 나올때까지 트리의 하단으로 이동을 합니다. 이때, 현재 탐색 중인 노드의 값과 추가할려는 값을 비교해서, 추가할 값이 더 크면 오른쪽 자식으로 이동, 값이 더 작으면 왼쪽 자식으로 이동하면서 Leaf Node를 찾습니다. Leaf Node를 찾으면, 해당 노드보다 추가할려는 값이 작으면 추가할려는 값은 찾은 Leaf Node의 왼쪽 자식이되고, 값이 더 크면 오른쪽 자식이 됩니다.
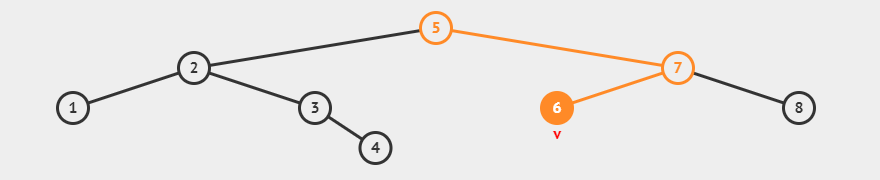
만약에 숫자들 2,3,4,7,8,1,6를 적혀 있는 순서 대로 값을 추가해서 이진 탐색 트리를 생성하면 다음과 같은 트리가 생성될 것 입니다.
노드 삭제하기
이진 탐색 트리에서 노드를 추가하는 것은 간단하지만, 삭제하는 것은 조금 더 복잡하니다. 왜냐하면, 노드를 삭제한 후, 삭제할 노드의 자리를 대체할 노드를 찾아서 위치를 바꿔줘야하기 때문입니다. 노드를 삭제할 때 고려해야되는 Case들을 3개로 나눠서 보도록 하겠습니다.
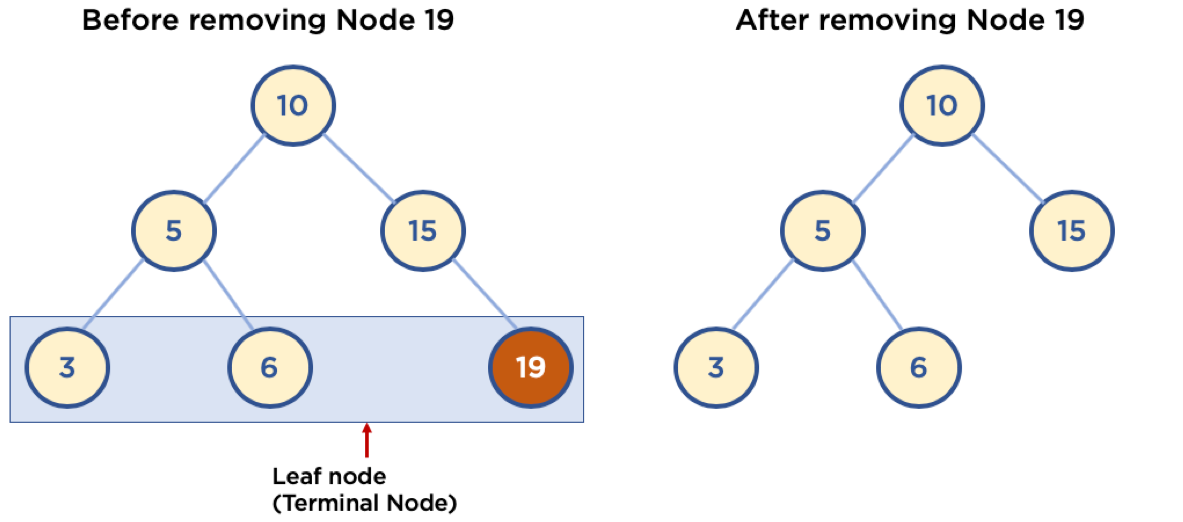
Case 1: 삭제할 노드가 Leaf Node 일때
이러한 Case는 간단합니다. Leaf Node이면 자식 노드가 없으므로, 삭제할 노드를 자신의 하위에 있는 서브 트리 중의 노드 하나로 대체할 필요가 없기 때문입니다. 노드를 삭제하고, 삭제한 부모 노드의 자식 노드만 갱신시켜주면 됩니다.
(http://www.fun-coding.org/00_Images/tree_remove_leaf.png)
# Case 1
if node.left == None and node.right == None: # 삭제할 노드가 Leaf Node 일때
if parent.left.value == node.value: # 부모 기준 삭제될 노드가 왼쪽 자식 일때 -> 왼쪽 자식은 삭제되므로 None으로 갱신
parent.left = None
return True
if parent.right.value == node.value:# 부모 기준 삭제될 노드가 오른쪽 자식 일때 -> 오른쪽 자식은 삭제되므로 None으로 갱신
parent.right = None
return True
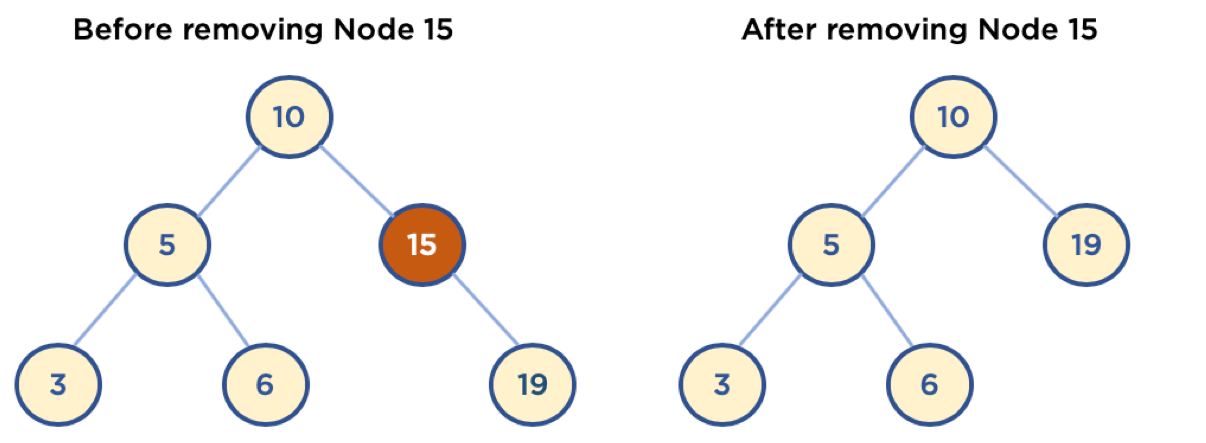
return FalseCase 2: 삭제할 노드가 자식 노드 하나를 갖고 있을때
Case 2 같은 경우에는, 원하는 노드를 삭제한 후, 삭제한 노드의 자릴 자식 노드로 대체하고, 삭제한 노드의 부모 노드의 자식 노드를 갱신시켜주면 됩니다. 삭제한 노드의 유일한 자식 노드로 대체 할 경우, 자식 노드의 하위 서브 트리도 그대로 유지되고, 이진 탐색 트리의 규칙에도 어긋나지 않기 때문에 고려할 부분들이 많지 않습니다.
삭제할 노드가 부모 노드의 왼쪽 자식인지 오른쪽 자식인지, 그리고 삭제할 노드가 왼쪽 자식만 있는지 오른쪽 자식만 있는지 확인하면 됩니다.
(http://www.fun-coding.org/00_Images/tree_remove_1child.png)
# Case 2
if node.left != None and node.right == None: # 삭제할 노드가 왼쪽 자식만 갖고 있을때
if parent.left != None:
if parent.left.value == node.value: # 삭제할 노드가 부모 노드의 왼쪽 자식일때
parent.left = node.left
return True
if parent.right != None:
if parent.right.value == node.value: # 삭제할 노드가 부모 노드의 오른쪽 자식일때
parent.right = node.left
return True
return False
elif node.left == None and node.right != None: # 삭제할 노드가 오른쪽 자식만 갖고 있을때
if parent.left != None:
if parent.left.value == node.value: # 삭제할 노드가 부모 노드의 왼쪽 자식일때
parent.left = node.right
return True
if parent.right != None:
if parent.right.value == node.value: # 삭제할 노드가 부모 노드의 오른쪽 자식일때
parent.right = node.right
return True
return FalseCase 3: 삭제할 노드가 자식 노드 두개를 갖고 있을때
(http://www.fun-coding.org/00_Images/tree_remove_2child.png)
이진 탐색 트리에서 노드를 삭제할때 고려할것이 가장 많은 Case 입니다. 그러한 이유는 이진 탐색 트리의 규칙 때문입니다. 값을 추가할때, 특정 노드보다 추가할 값이 크면 오른쪽 자식으로, 값이 작으면 왼쪽 자식으로 저장하는 규칙 때문에 자기 자신의 노드보다 오른쪽 서브 트리에 있는 모든 노드들은 자기 자신보다 값들이 무조건 커야하고, 반대로 왼쪽 서브 트리에 있는 모든 노드들은 값들이 작아야 합니다. 다음 트리를 한 번 보도록 하겠습니다.
(http://www.fun-coding.org/00_Images/tree_remove_2child_code_left.png)
보다시피, 현재 자기 자신이 15 노드라고 했을때, 15보다 왼쪽에 있는 노드들은 모두 15보다 작고, 오른쪽에 있는 노드들은 모두 15보다 큽니다. 이러한 규칙은 노드를 삭제한 이후에도 유지되어야 하기 때문에 삭제한 노드를 대체할 노드를 찾는것이 가장 큰 문제점 입니다. 만약, 위의 트리에서 노드 15를 삭제하고 노드 17로 대체하면, 17의 오른쪽에는 노드 16이 여전히 있습니다. 하지만, 노드 17의 오른쪽에 있는 노드들은 모두 17보다 커야하기 때문에 16은 오른쪽에 있으면 안됩니다. 그렇기 때문에, 규칙을 유지하면서 대체할 노드를 찾는 것이 가장 중요합니다.대체할 노드를 찾는 방법은 두가지가 있습니다.
- 삭제할 노드의 오른쪽 서브트리에서 가장 작은 노드로 대체하기(-> 위의 트리에서는 16)
- 삭제할 노드의 왼쪽 서브트리에서 가장 큰 노드로 대체하기(-> 위의 트리에서는 14)
위의 두가지 방식으로 찾은 노드들로 대체하면 이진 탐색 트리의 규칙을 유지할 수 있습니다. 저희는 1번 방식을 통해 대체할 노드를 찾아보도록 하겠습니다.
1번 방식으로 노드를 찾는 방법은 다음과 같습니다:
1. 삭제할 노드의 오른쪽 자식을 찾습니다.
2. 삭제할 노드의 오른쪽 자식으로 부터 Leaf Node가 나올때까지 계속 왼쪽 자식으로 이동합니다.
3. 이렇게 찾은 Leaf Node는 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 노드가 될 것 입니다.
삭제할 노드가 A, 대체할 노드를 B, A의 부모 노드를 C, A의 왼쪽 자식 노드를 D, A의 오른쪽 자식 노드를 E라고 하겠습니다.
A를 B로 대체하기 위해서는 C->B를 가르키고, B->D && B->E를 자식 노드들로 가르키도록 하면 됩니다.
# Case 3
if node.left != None and node.right != None: # 자식 노드가 왼쪽 오른쪽 자식 모두 있을때
replacement = node.right
replacement_parent = node
while replacement.left != None: # 오른쪽 서브 트리에서 가장 작은 노드 찾기; B 찾기
replacement_parent = replacement
replacement = replacement.left
replacement_parent.left = replacement.right #대체한 노드의 부모 노드의 자식 노드 갱신하기
# 대체할 노드의 자식들 갱신 시켜주기
replacement.left = node.left # B->D 가르키기
replacement.right = node.right # B->E 가르키기
if parent.left != None:
if parent.left.value == node.value: # 삭제한 노드가 부모 노드의 왼쪽 자식일때
parent.left = replacement # 삭제한 노드의 부모 노드의 자식 노드 갱신하기; C->B 가르키기
return True
if parent.right != None:
if parent.right.value == node.value: # 삭제한 노드가 부모 노드의 오른쪽 자식일때
parent.right = replacement # 삭제한 노드의 부모 노드의 자식 노드 갱신하기; C->B 가르키기
return True
return False시간 복잡도
트리의 depth/높이를 h라고 했을때, 시간 복잡도는 O(h)가 됩니다. 이때, 트리가 n개를 가지고 있으면 h = log n 에 가깝기 때문에 시간 복잡도는 O(log n)이 됩니다. 하지만, 이는 평균 시간 복잡도를 뜻합니다.
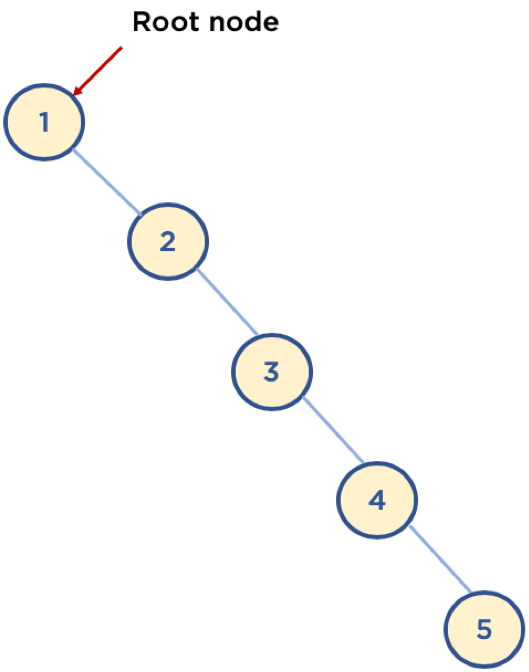
이진 탐색 트리는 최악의 경우 O(n)의 시간 복잡도를 가지게 됩니다. 왜냐하면, root에 n개의 값들 중 가장 작은 값이 들어가고, 추후에 추가되는 값들이 이전에 추가된 값들 보다 모두 큰 값이 들어오면 결국 모든 노드는 오른쪽 자식만 갖게 됩니다.
(http://www.fun-coding.org/00_Images/worstcase_bst.png)
이런 경우에는 결국 배열과 동일하기 처음부터 순차적으로 하나씩 탐색해서 원하는 값을 찾게되기 때문에 시간 복잡도는 O(n)이 됩니다.
이렇게 한쪽으로만 데이터가 추가되는 것을 방지하기 위해 AVL 트리(Tree) 처럼 좌우로 균형을 맞춰주는 트리가 있습니다.