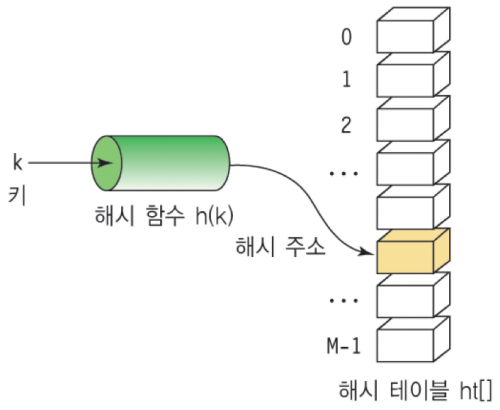
해쉬 테이블(Hash Table)은 저장할 데이터(Value)와 매칭되는 키(Key) 값을 Key-Value 형태로 같이 저장하는 데이터 구조로써, 원하는 데이터를 찾기 위해서 처음부터 순차적으로 배열을 훑어야하는 문제점을 해결합니다. 원하는 데이터를 찾고 싶은 경우, 데이터와 매칭되는 키 값을 통해 바로 원하는 데이터를 반환 받을 수 있습니다.
데이터를 저장하거나 읽기 빠르므로, 검색, 저장, 삭제, 읽기가 많이 일어나는 경우 사용하기 용이합니다.
(https://www.fun-coding.org/00_Images/hash.png)
용어
- 해쉬(Hash): 임의 값을 고정 길이로 변환하는 것
- 해쉬 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
*해싱 함수(Hashing Function): Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수- 해쉬 값(Hash Value) 또는 해쉬 주소(Hash Address): Key를 해싱 함수로 연산해서, 해쉬 값을 알아내고, 이를 기반으로 해쉬 테이블에서 해당 Key에 대한 데이터 위치를 일관성있게 찾을 수 있음
- 슬롯(Slot): 한 개의 데이터를 저장할 수 있는 공간
구현하기(파이썬)
hash_table = list([0 for i in range(8)])
def get_key(key):
return hash(key) # hash() -> 파이썬에 제공해주는 Hash Key 값을 반환해주는 함수
def hash_function(key):
return key % 8
def save_data(key, value):
hash_address = hash_function(get_key(key))
hash_table[hash_address] = value
def read_data(key):
hash_address = hash_function(get_key(key))
return hash_table[hash_address]
- hash_table : 크기가 8인 해쉬 테이블
- def get_key(key) : 파이썬에서 제공해주는 hash() 메서드를 이용해서 키 값을 해쉬로 변환
- def hash_function(key) : 해쉬 값을 해쉬 테이블에 저장할 위치인 해쉬 주소로 변환
- def save_data(key, value) : 저장할 Key-Value 값을 받아서, 키 값은 해쉬 주소로 변환하고, 변환된 해쉬 주소에 Value 값을 저장
- def read_data(key): 찾고 싶은 데이터의 키 값을 해쉬 주수로 반환하고, 해쉬 테이블에서 해당 주소의 값을 가져와서 찾고자 하는 데이터 반환
문제점:
해쉬 테이블의 가장 큰 문제점은 같은 해쉬 주소에서 다수의 데이터를 저장하고자 할때 충돌이 일어난다는 문제점입니다. 위의 코드에서 해쉬 테이블의 크기는 8인데, 만약 저장하고자하는 데이터의 갯수가 8개를 초과하게 되면 무조건 충돌이 일어납니다. 또한, 적은 양의 데이터를 저장할려고해도, 해쉬 주소는 겹칠수 있기 때문에 이러한 경우에도 충돌이 일어납니다.
다음으로는 충돌이 일어나지 않는 해결 방법 두가지를 알아보도록 하겠습니다.
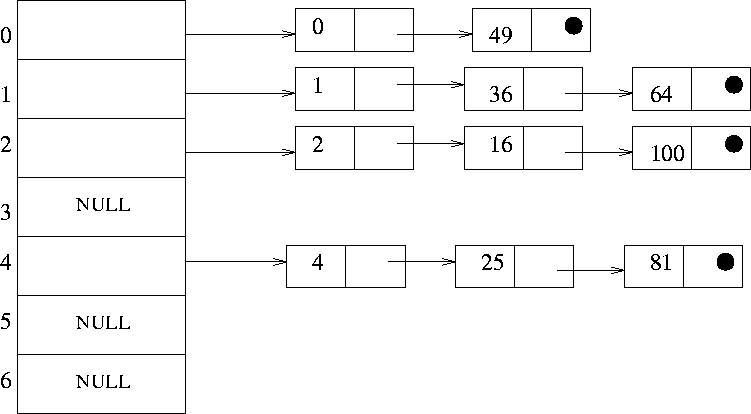
충돌 해결 #1: Chaining 기법
해당 방식은 Open Hashing 기법 중 하나입니다. Open Hashing이란, 해쉬 테이블 외의 공간을 이용해서 데이터를 저장하는 방식입니다. Chaining 기법은 각 해쉬 주소마다 다수의 데이터를 저장할 수 있도록 하며, 각 데이터를 키-데이터 값으로 저장합니다. C언어서는 연결 리스트, Java에서는 ArrayList<>()로 구현 가능 합니다.
구현하기(파이썬)
hash_table = list([0 for i in range(8)]) # 해쉬 테이블의 값들을 0으로 초기화해서 선언
def get_key(data):
return hash(data)
def hash_function(key):
return key % 8
def save_data(data, value):
key = get_key(data)
hash_key = hash_function(key)
if hash_table[hash_key] == 0:
hash_table[hash_key] = [[key, value]]
else:
for v in hash_table[hash_key]:
if v[0] == key: # 이미 버킷에 같은 Key 값을 가진 데이터가 있을때 Value를 업데이트 해줌
v[1] = value
return
hash_table[hash_key].append([key, value]) # 버킷에 같은 Key 값을 가진 데이터가 없으면 데이터를 추가해줌
def read_data(data):
key = get_key(data)
hash_key = hash_function(key)
if hash_table[hash_key] != 0:
for v in hash_table[hash_key]:
if v[0] == key:
return v
return "Data Not Found"
else:
return "Data Not Found"
- def save_data(data,value)에서 먼저 해당 해쉬 주소에 값이 저장되어 있는지 확인 합니다. 해쉬 주소에 저장된 값이 없으면 Key-Value 값을 가진 튜플을 배열에 저장 시킵니다. 이렇게 함으로써, 같은 해쉬 주소에 다수의 값이 저장될때 [[Key, Value], [Key, Value], [Key, Value]...] 로 값들이 저장될 수 있도록 합니다.
먄약 해쉬 주소에 이미 저장된 값들이 있으면, 같은 Key 값을 가진 튜플이 있는지 확인 합니다. 만약 있으며 Value 값을 갱신 시켜주고, 값이 없으면 새로운 [Key-Value] 값을 추가해줍니다.- def read_data(data) 에서는 먼저 Key 값을 해쉬랑 해쉬 주소로 변환합니다. 그 다음으로 해쉬 테이블에서 해당하는 해쉬 주소에 저장된 튜플들을 순회하면서, 해쉬를 Key 값으로 가진 튜플이 있는지 확인합니다. 일치하는 튜플이 있을 경우 Value를 반환합니다.
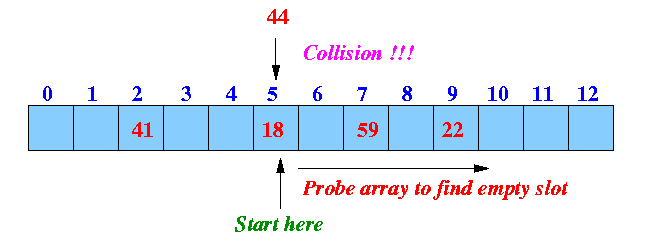
충돌 해결 #2: Linear Probing 기법
Linear Probing 기법은 Closed Hashing 기법 중 하나로써, 해쉬 테이블 외의 추가의 저장공간을 필요로 하지 않기 때문에 저장공간 활용도를 높일 수 있습니다. Linear Probing 기법은 데이터를 저장할려고 할때 충돌이 일어나면, 해당 해쉬 주소로 부터 순차적으로 하나씩 다음 주소를 확인해서 빈 공간을 찾습니다. 그렇게 맨 처음으로 나온 빈 공간에 충돌이 일어났었던 데이터를 저장하는 기법입니다.
구현하기(파이썬)
hash_table = list([0 for i in range(8)])
def get_key(data):
return hash(data)
def hash_function(key):
return key % 8
def save_data(data, value):
key = get_key(data)
hash_key = hash_function(key)
hash_size = len(hash_table)
for k in range(hash_key, hash_key+hash_size):
if hash_table[k % hash_size] == 0:
hash_table[k % hash_size] = [key, value]
return
elif hash_table[k % hash_size][0] == key:
hash_table[k % hash_size][1] = value # Key 값이 같으면 Value를 업데이트 해줌
return
return "Hash Table is Full"
def read_data(data):
key = get_key(data)
hash_key = hash_function(key)
hash_size = len(hash_table)
for k in range(hash_key, hash_key+hash_size):
if hash_table[k % hash_size] == 0:
continue
if hash_table[k % hash_size][0] == key:
return hash_table[k % hash_size]
return "Data Not Found"먼저, 데이터와 매칭되는 해쉬 주소에 데이터 저장을 시도합니다. 충돌이 일어나면 하나씩 다음 주소를 탐색해서 빈 공간을 찾고, 데이터를 저장합니다. 이때, 저장하는 데이터는 Key-Value 값인데, 그러한 이유는 데이터를 찾을때 Key 값이 필요하기 때문입니다.
데이터를 찾기 위해서는 우선 Key 값에 매칭되는 해쉬 주소를 확인합니다. 이때, 해당 해쉬 주소의 Key 값을 확인한 후, 일치하면 Value를 반환합니다. 일치하지 않을 경우, 하나씩 다음 해쉬 주소의 Key 값을 확인하면서, 일치하는 Key 값이 나올때까지 탐색합니다.
시간 복잡도
저장과 읽기를 할 때, 충돌이 일어나지 않으면 시간 복잡도는 O(1)이 됩니다. 왜냐하면, 충돌이 없을 경우 정확히 하나의 해쉬 주소를 보면 되기 때문입니다. 하지만, N개의 데이터를 저장하거나 읽을때, 모든 데이터에 대해서 충돌이 일어나면 시간 복잡도는 O(n)이 됩니다. 왜냐하면, 모든 데이터에 대해 충돌이 일어나면, 결국 배열에 순차적으러 N개의 데이터를 저장하거나 읽는 것과 똑같이 실행되기 때문입니다.