3.3 Pulse Shaping Filter

3.1~3.2 포스팅을 통해 디지털 통신의 송수신부 구조를 살펴 보았다.

여태까지는 송신부에서 비트를 심볼로 매핑하고 unit energy pulse를 통해 신호를 만들도록 설명했다.

그러나 unit energy pulse가 과연 최적의 신호를 만드는 pulse 일까? 답은 아니다. 그 이유를 알기 위해 아래 그림을 살펴 보자.

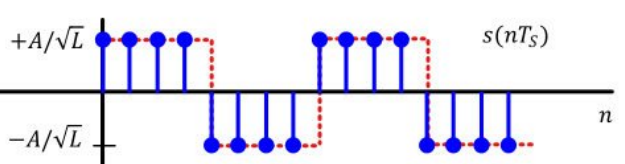
위 그림은 unit energy pulse 또는 직사각형 펄스를 통해 심볼을 신호로 바꾼 그림이다.

시간 축에서 신호를 분석해보면 첫 번째 심볼에 대한 신호와 두 번째 심볼에 대한 신호는 시간 축에서 명확히 분리되어 있다.

이를 곧 심볼 간 간섭(ISI - Inter Symbol Interference)가 없다고 정의한다.

직사각형 펄스를 푸리에 변환을 통해 주파수 축에서 보면 sinc함수가 된다. 아래 식과 같다.

sinc함수에서 null이 되는 구간은 $\frac{1}{T_M}$간격으로 나타나게 된다. 그리고 유효한 주파수 범위는 아래와 같다.

심볼 당 샘플 $L=8$ 일 때 직사각형 펄스의 스펙트럼은 아래와 같다.

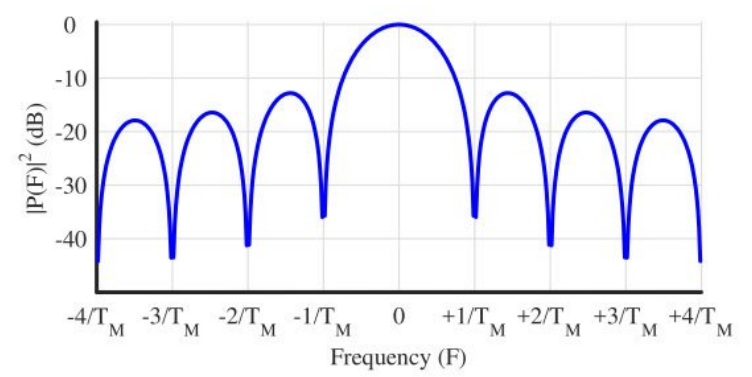
스펙트럼 크기를 살펴보면 피크 대비 두번째 피크의 크기가 -13dB 차이가 난다.

이는 곧 심볼을 직사각형 펄스를 통해 신호를 만들면 주파수 영역에서 신호가 -13dB의 크기를 가지며 전체 주파수 영역을 점유하게 된다.

일반적으로 주파수는 한정된 자원이기 때문에 한 신호가 넓은 주파수 영역을 점유하면 다른 신호에 간섭을 일으킨다.

따라서 우리가 정말로 필요한 주파수 영역만을 사용하고 나머지 영역은 매우 낮은 크기로 감쇄시켜야 다른 신호에 간섭을 일으키지 않을 수 있다.

한 가지 다른 문제는 수신부에서 매치드 필터링을 할 때 일어난다.

넓은 대역폭을 갖는 신호는 매치드 필터링을 수행할 때 더 많은 잡음이 함께 들어오게 된다. 즉 신호의 품질이 떨어지게 된다.

이제 직사각형 펄스로 pulse shaping을 수행할 때의 문제점을 알게 되었다.

가장 큰 문제는 신호가 전체 주파수 대역을 차지 한다는 점이었다.

따라서 한정된 주파수 대역을 차지하도록 신호를 만드는 pulse shaping 필터를 알아보자.

일반적으로 시간 축에서 짧은 신호는 주파수 축에서 넓은 대역을 차지한다. 직사각형 펄스는 시간 축에서 짧게 위치하므로 넓은 대역을 차지하는 것이다.

반대로 시간 축에서 길게 존재하는 신호는 주파수 축에서 좁은 대역을 차지한다. 따라서 주파수 대역을 줄이기 위해 신호를 시간 축에 길게 위치시켜야 한다.

만약 직사각형 펄스의 길이를 2배 증가 시키면 주파수 축에서 점유하는 대역은 감소하겠지만 같은 시간에 더 적은 심볼을 보내게 된다.

이를 해결하기 위해서 나이퀴스트 필터가 도입됐다. 아래 그림을 참고해보자.

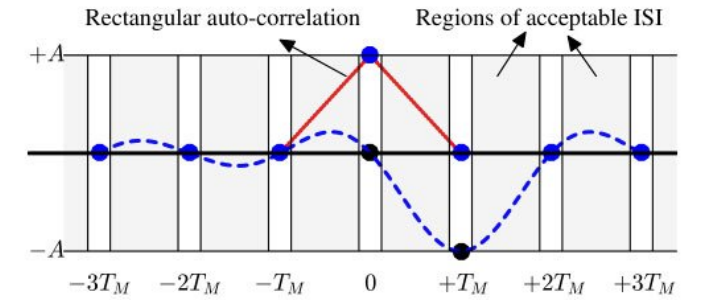
파란색 점선 신호는 나이퀴스트 필터로 pulse shaping된 한 개의 심볼에 대한 신호이다.

직사각형 펄스 신호에서 한 개의 심볼에 대한 신호는 해당 심볼 기간에만 존재하고 인접한 심볼 기간에는 0이다. 즉 인접한 심볼에 영향을 주지 않지만 넓은 주파수 대역을 차지한다.

그러나 나이퀴스트 펄스 신호에서는 한 개의 심볼에 대한 신호가 여러 심볼 주기에서 위치한다. 그러나 심볼 주기 $T_M$에서 값은 0으로 존재한다.

따라서 인접한 심볼에 영향을 주지 않으면서도 시간 축에서 넓게 위치하기 때문에 좁은 주파수 대역을 가질 수 있게 된다.

즉 시간 축에서 인접한 심볼 위치에서 심볼에 대한 신호가 0을 만족하는 pulse shaping 필터를 나이퀴스트 필터라고 한다. 아래 그림에서 확인 할 수 있다.

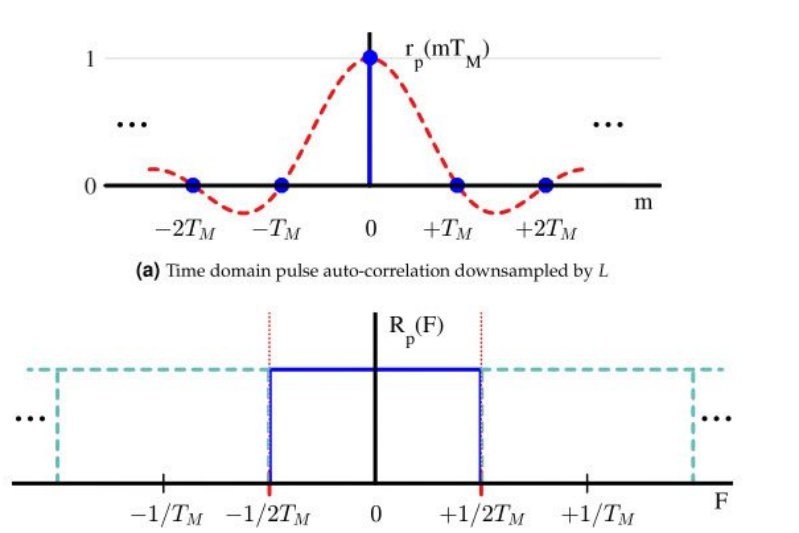
인접한 심볼 위치에서 값이 0인 것을 확인 할 수 있다.

나이퀴스트 필터중 대표적인 것이 sinc 함수이다. sinc 함수는 심볼 주기 $T_M$간격으로 값을 0으로 만들 수 있기 때문에 ISI를 없앨 수 있다.

그러나 여기서 우리는 두가지 문제점을 생각해봐야 한다.

첫 번째로 sinc함수는 시간축에서 무한히 이어지는 함수다. 무한한 계수를 갖는 필터는 구현할 수 없다.

따라서 sinc함수의 꼬리 부분을 잘라서 무한개의 계수를 유한개로 만들어야 한다.

두 번째로 DAC와 ADC 클럭은 다르다. 따라서 샘플링 주파수의 오차로 인해 최적의 심볼 위치에서 샘플링 할 수 없다. 심볼 간격$T_M$에서 조금 이라도 벗어난다면 심볼 간 간섭이 발생하여 신호의 품질에 오류를 줄 수 있다.

따라서 sinc함수의 꼬리 부분의 크기 감쇄를 빠르게 주어 영향을 최소한으로 줄여야 한다.

정리하자면 무한개의 sinc 함수의 필터 계수를 유한개로 바꾸면서 동시에 시간 축에서 꼬리 부분의 감쇄를 빠르게 수행해야 한다.

이를 달성하기 위해 Raised Cosine 필터가 제시 된다.

Raised Cosine 필터는 Sinc 필터에 비해 좀 더 넓은 주파수 대역을 점유한다. 아래 그림을 살펴 보자.

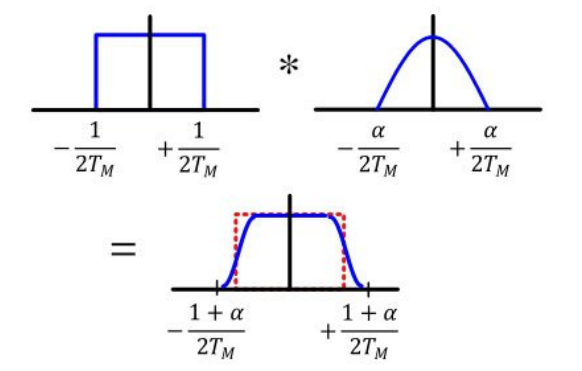
스펙트럼 모양이 직사각형인 것은 sinc 필터의 스펙트럼 모양이고, 컨볼루션 결과로 나온 스펙트럼은 Raised Cosine 필터의 스펙트럼 모양이다.

Raised Cosine 필터의 스펙트럼이 점유하는 주파수 대역이 좀 더 넓은 것을 확인할 수 있다.

이 때 $\alpha$만큼의 대역폭이 추가되었는데 이를 rol-off factor라고 정의한다.

만약 $\alpha = 1$일 때는 최소 대역폭 대비 100%의 더 넓은 대역폭을 차지한다는 뜻이다. 반대로 $\alpha =0.25$일 때는 최소 대역폭 대비 25% 더 넓은 대역폭을 차지한다는 뜻이다.

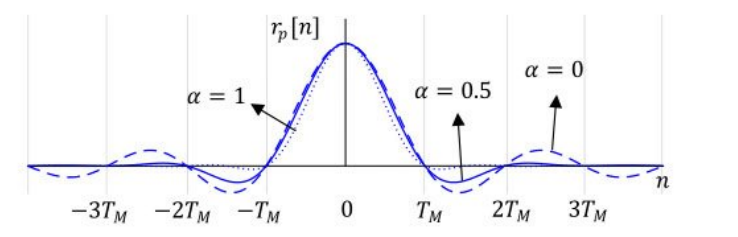
위 그림을 살펴보면 $\alpha =0$일 때는 sinc함수의 파형이고 $\alpha \neq 0$일 때는 Raised cosine의 파형이다.

roll off factor가 클 수록 스펙트럼 상에서는 더 넓은 대역폭을 차지하고, 더 빨리 감쇄 된다. 따라서 roll-off가 클수록 ADC/DAC 샘플링 클럭 차이 등으로 발생할 수 있는 ISI에 강인해진다.

그러나 한 가지 더 고려해야 할점은 송신부에서 Raised Cosine 필터를 통해 보내기만 하면 수신부에서 매치드 필터링을 무엇으로 하냐에 대한 질문이 생긴다.

따라서 Raised Cosine 필터를 루트를 취한 Square Root Raised Cosine(SRRC) 필터를 만들 수 있다.

따라서 송신부와 수신부에 각각 SRRC 필터를 분리해서 두고 Pulse Shaping 및 Matched Filtering 을 수행한다.

아래는 SRRC 필터의 임펄스 응답이다.

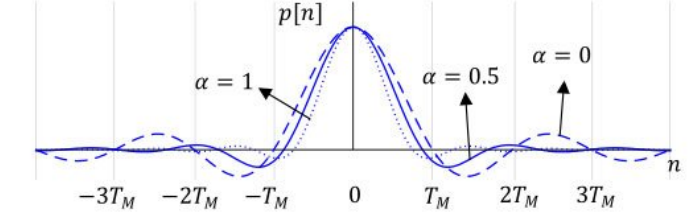
위 그림에서 확인할 수 있듯이 심볼 위치해서 값이 0이 아니다. 즉 나이퀴스트 필터 조건을 위배한다. 하지만 당연하다.

수신부에서 매치드 필터링까지 해야 결과가 Root Raised Cosine 필터가 되어 나이퀴스트 필터 조건을 만족하게 된다. 따라서 ISI를 제거할 수 있다.

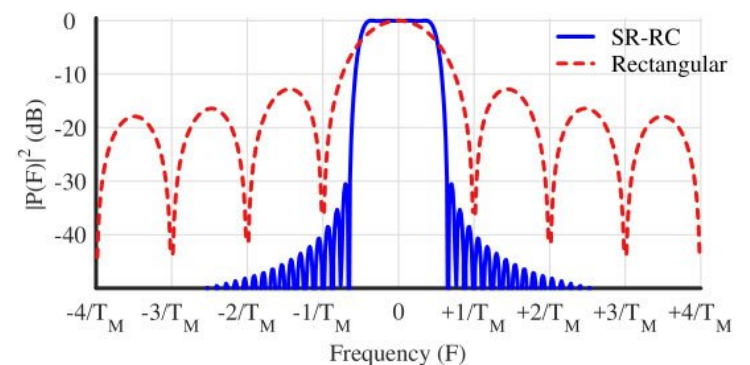
위 그림은 pulse shaping-matched filtering의 컨볼루션 결과를 주파수 축에서 나타낸 것이다.

Rectangular pulse shaping을 사용했을 때보다 SRRC Matched Filtering 한 결과가 스펙트럼 상에서 더 많이 감쇄됨을 확인할 수 있다.