3.5 Stethoscopes for a communication system

통신 모뎀의 성능을 평가하기 위해서 다양한 도구들이 존재한다.

가장 먼저 Eye Diagram에 대해 알아보자. 이를 이해하기 위해 아래 그림을 살펴보자.

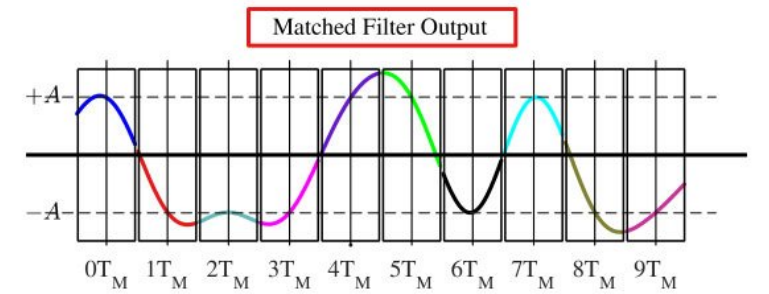
위 파형은 SRRC Matched Filtering된 결과이다.

시간 축에서 심볼 간격 $T_m$ 의 앞 뒤로 절반의 심볼 간격인 $\frac{1}{2}T_M$ 씩 선택해 영역을 구분하면 위 그림의 시간 축과 같다.

검정색 박스는 $-\frac{1}{2}T_M$ ~ $\frac{1}{2}T_M$, $\frac{1}{2}T_M$ ~ $\frac{3}{2}T_M$ ,... 간격으로 구분되어 있다.

이 구간에 해당하는 신호는 구분을 위해 다른 색으로 표시되어 있다. 만약 이 신호들을 모두 겹쳐서 그리면 어떻게 될까? 아래 그림을 살펴보자.

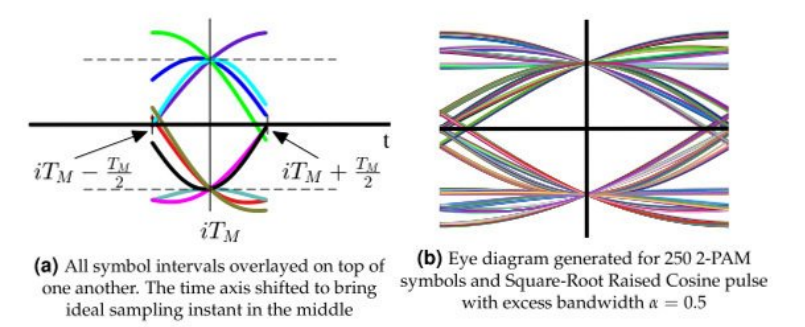
위 그림은 신호를 모두 겹쳐 그렸을 때 나오는 모양이다. 이것을 Eye Diagram이라고 한다.

즉 심볼 주기 $T_M$을 기준으로 앞뒤로 절반 심볼주기 $0.5T_M$만큼의 신호를 모두 겹쳐 그렸을 때 나오는 파형을 Eye Diagram이라고 한다.

위 그림의 (b)는 총 200개 구간의 모든 신호를 겹쳤을 때 나오는 파형이다.

Eye Diagram은 채널 환경과 심볼 간 간섭이 수신 신호에 미친 영향을 분석하는 데 유용하다. 아래 그림을 살펴보자.

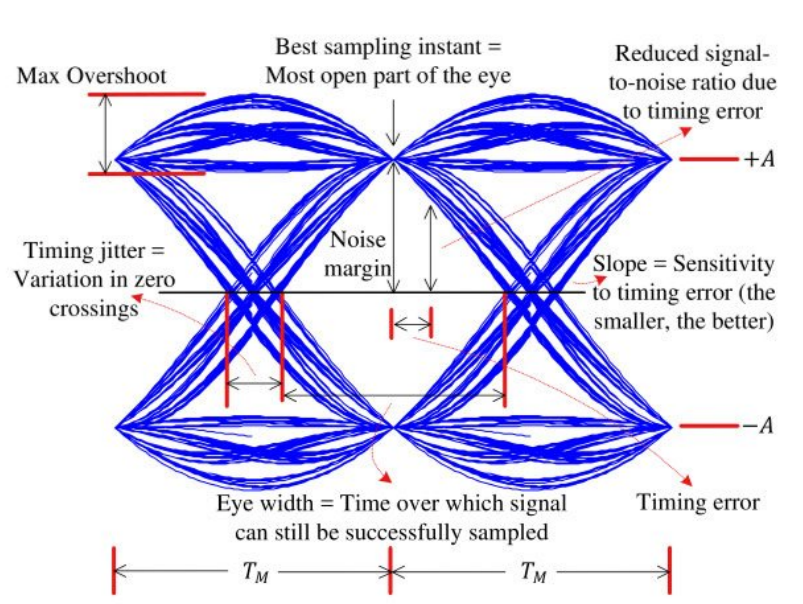
위 그림은 2개의 심볼 주기에 해당하는 Eye Diagram을 나타내었다. 위 그림을 통해 다양한 정보를 알 수 있다.

가장 먼저 최적의 샘플링 타이밍을 알 수 있다. SRRC-Matched Filtering의 경우 심볼 간 간섭이 없기 때문에 Eye Diagram에서 그림이 모이는 지점이

심볼 위치에 해당하는 샘플링 타이밍이다. 그 밖에 그림에 해당하는 다양한 정보를 유추할 수 있다.

두 번째로 Constellation Point의 산점도(Scatter plot)이다.

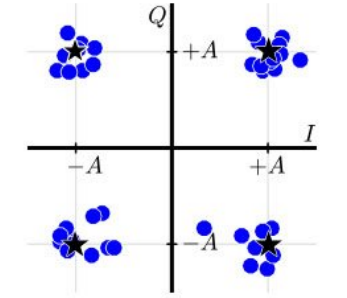
위 그림은 매치드 필터링의 결과 신호에서 심볼 주기로 추출된 샘플을 각각 복소 평면에 나타낸 것이다. 기준 별자리로 부터 멀어질 수록 SNR이 나빠진 것을 알 수 있다.

이 때 기준 별자리로 부터 수신된 심볼이 떨어진 거리를 EVM(Error-Vector-Magnitude)라고 정의한다.

세번째는 비트 오류 확률(Bit-Error-Rate)이다.

무선 통신 시스템에서 비트 오류 확률과 심볼 오류 확률을 아래와 같이 정의한다.

심볼 오류 개수를 결정 짓는 것은 무선 채널의 노이즈가 신호 대비 얼마나 큰 지에 따라 결정된다. 이를 SNR(Signal to Noise Ratio)라고 한다.

따라서 SNR에 따른 비트/심볼 오류 개수를 그래프로 그릴 수 있다. 그 전에 먼저 SNR의 정확한 정의를 알아보자.

$P_M$은 신호의 전력이고 $P_w$는 노이즈의 전력이다. 이 때 신호 전력 $P_M$은 변조된 심볼의 평균 에너지 이다. 식으로 나타내면 아래와 같다.

$E_M$은 변조된 심볼의 평균 에너지이고 $T_M$은 심볼 주기 이다.

만약 PAM 또는 QAM 변조의 경우 심볼 평균 에너지는 아래와 같다.

노이즈 전력은 신호의 대역폭 $B$ 당 노이즈 전력을 의미한다.

따라서 SNR 식을 아래와 같이 다시 쓸 수 있다.

만약 M-QAM 또는 M-PAM의 경우 $log_2M$ 비트가 1개의 심볼이기 때문에 비트 에너지는 아래와 같다.

그리고 비트 레이트 $R_b$는 아래와 같이 정의 된다.

따라서 비트 에너지당 노이즈 전력인 $E_b/N_o$는 아래와 같이 정의된다.

일반적으로 무선 통신 모뎀의 송신부에서 비트는 심볼로 변환된다.

만약 M값이 변하면 평균 심볼 에너지는 변화한다. 따라서 이 값을 normalized 해주는 것이 필요하다. 방법은 간단하다.

바로 Normalized하기 전 평균 심볼 에너지의 루트 값을 나눠주는 것이다. 실제로 위 심볼의 평균 심볼 에너지를 구해보면 1이다.

해당 과정을 통해 M값에 관계 없이 심볼 에너지가 1인 변조를 수행할 수 있다.

일반적으로 모뎀의 송신부에서는 Pulse Shaping을 수행하기 위해 심볼을 upsampling 한다. 따라서 upsampling된 심볼의 평균 에너지는 $L$이다.

따라서 SRRC Pulse Shaping필터의 Peak값도 이에 맞게 조절해줘야 한다. SRRC Pulse Shaping 필터의 peak를 $p[0]$라고 하면 아래와 같다.

노이즈의 전력에 대해 조금 더 살펴보자.

일반적으로 모뎀을 설계할 때 심볼 레이트 $R_M$은 변화시키지 않고 다른 파라미터들을 변화시킨다. 그 이유는 심볼 레이트는 신호의 대역폭과 직접적으로 연관이 있기 때문이다. 일반적으로 신호의 대역폭은 정해져있기 때문에 심볼 레이트를 변화시키지 않는다.

따라서 편의를 위해 SNR을 계산할 때 $R_M=1$ 로 고정시킬 수 있다.

노이즈의 전력을 다시 써보면 아래와 같다.

신호의 대역폭은 Aliasing 때문에 Sample Rate 가$\frac{F_S}{2}$를 넘을 수 없다.

그리고 샘플레이트 $F_S$는 $F_S = \frac{L}{T_M}$을 만족한다. $\frac{1}{T_M} = R_M = 1$로 고정하면 위 식과 같이 변형할 수 있다. $L$은 심볼 당 샘플 수이다.

따라서 심볼 당 샘플 수가 $L$이고 M으로 변조된 신호에 대한 노이즈 파워는 아래와 같다.

Normalized한 심볼로 생성한 신호의 전력과 노이즈의 전력이 모두 심볼 당 샘플 $L$에 비례하므로 snr을 계산할 때 분자와 분모에 모두 $L$이 존재한다.

따라서 이 값은 상쇄된다.