3.4 Quadrature Amplitude Modulatioin (QAM)

QAM 변조 방식을 이해하기 위해서 먼저 baseband signal과 passband signal에 대해 이해할 필요가 있다.

Baseband 신호는 신호의 스펙트럼이 주파수 0 근처에 위치한 신호이다. 아래 그림은 Baseband 신호의 예이다.

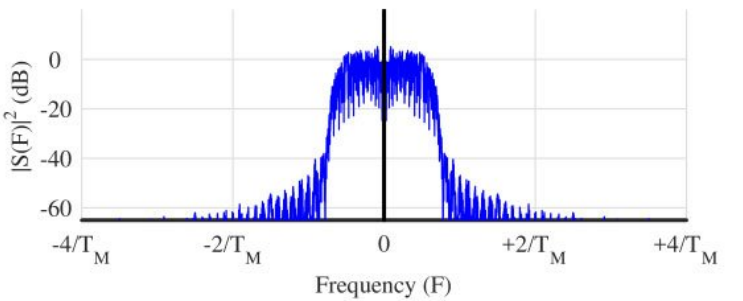
위 그림은 200개의 PAM 변조된 심볼을 SRRC Pulse Shaping 필터링한 신호의 스펙트럼 모양이다.

신호의 스펙트럼이 0 근처에 위치하기 때문에 baseband signal이다.

일반적으로 무선 통신에서는 통신 하기 위한 주파수 대역이 존재하기 때문에 baseband에 위치한 신호를 더 높은 주파수로 옮겨줘야 한다.

이를 passband signals 이라고 한다.

일반적으로 정현파 함수를 baseband 신호에 곱해서 baseband 신호를 passband 신호로 옮길 수 있다.

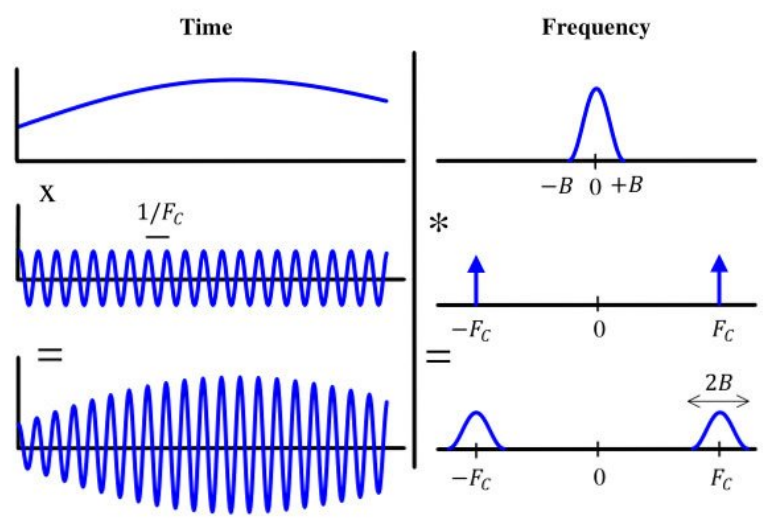
위 그림에서 PAM 변조 및 Pulse Shaping된 신호가 시간 축 및 주파수 축 상에서 나타났다. baseband에 신호가 위치한다.

여기서 주기가 $\frac{1}{F_C}$ 인 정현파를 시간 축에서 곱해준다. 시간 축에서의 곱은 주파수 축에서 convolution 이므로 신호의 중심대역이 $F_C$로 이동한 것을 볼 수 있다.

이 때 곱해진 정현파를 반송파(carrier)라고 부른다.

위 그림에서는 baseband 신호를 paseband 신호로 바꾸기 위해 cos을 반송파로 사용하였다. 그러나 정현파에는 sin도 존재한다.

시간 축에서 cos과 sin은 직교하기 때문에 baseband 신호를 cos과 sin으로 동시에 곱해 passband 신호로 만들어도 서로 간섭이 발생하지 않는다.

이 점에서 QAM 변조가 탄생 하였다. cos 반송파와 sin 반송파에 각각 다른 신호를 곱해준다면 서로 간섭이 없으면서도 전송률을 올릴 수 있게 된다.

이제 4-QAM 변조를 사용한 모뎀의 송신부를 아래 그림에 나타내었다.

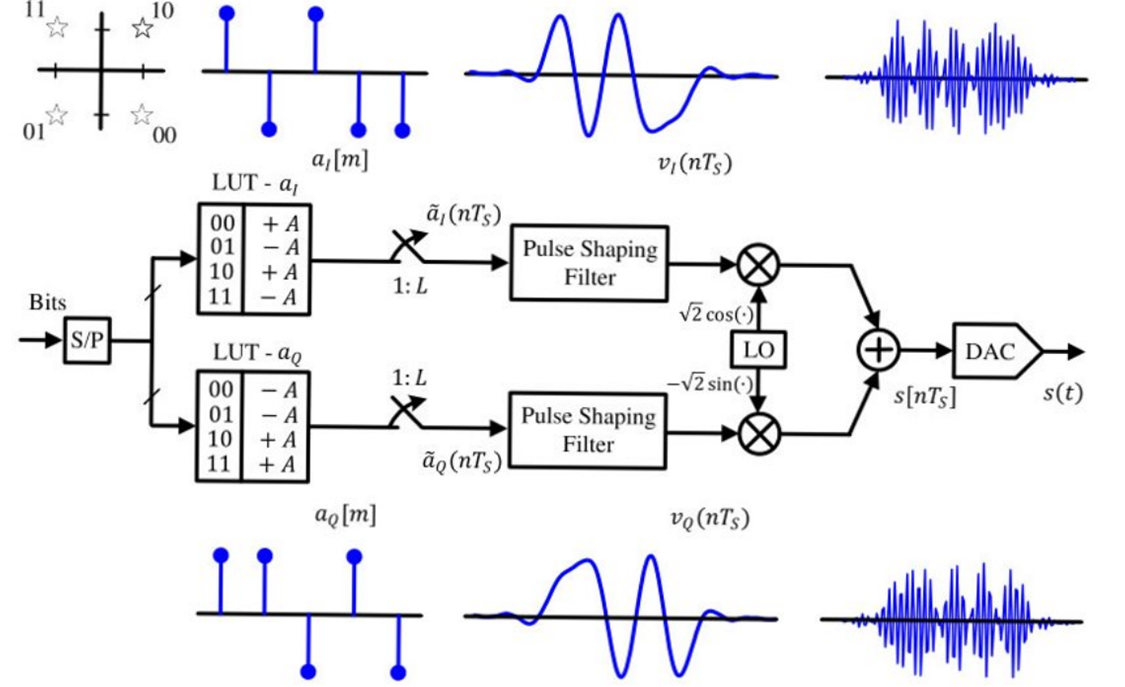
예를 들어 비트가 00이 들어오면 실수 심볼은 $+A$를 허수 심볼은 $-A$를 만드는 식이다.

만약 비트가 01이 들어오면 실수 심볼은 $-A$ 허수 심볼은 $-A$를 만든다.

4-PAM 변조는 2개의 비트를 1개의 심볼에 매핑했다면 4-QAM 변조는 2개의 비트를 각각 실수부 심볼과 허수부 심볼에 매핑한 것이다.

만들어진 실수부 심볼과 허수부 심볼은 심볼 당 샘플 $L$만큼 upsampling 하여 $\tilde{a}_I[m]$과 $\tilde{a}_Q[m]$를 만든 뒤 SRRC Pulse Shaping을 진행한다.

Pulse Shaping 후 출력된 신호 $v_I(nT_S)$와 $v_Q(nT_S)$는 아래 식 처럼 나타낼 수 있다.

위 식을 심볼 인덱스로 다시 표현하면 아래 식과 같다.

$v_I(nT_S)$와 $v_Q(nT_S)$는 baseband에 위치한 신호기 때문에 정현파를 곱해 passband 신호로 바꿔줘야 한다. 이 때 실수부 신호에는 cos을 허수부 신호에는 sin을 곱한다. 그리고 정현파의 크기는 $\sqrt2$이고, 주파수는 $F_C$이다. 크기가 $\sqrt2$인 이유는 추후 설명한다.

따라서 생성된 신호 $s(nT_S)$는 아래와 같다.

신호 $s(nT_S)$가 DAC로 입력되어 나온 아날로그 신호 $s(t)$는 아래와 같다.

위 처럼 QAM 변조된 신호는 아래 그림처럼 나타낼 수 있다.

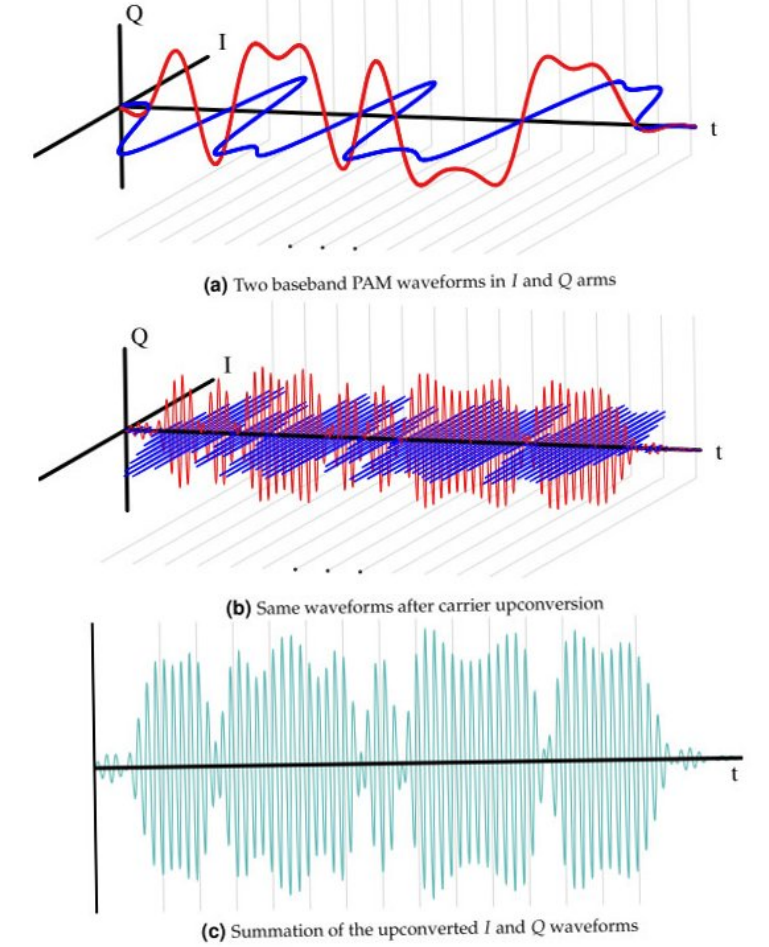
그림을 분석해보면 실수부 신호와 허수부 신호가 각각 복소 평면 직교 상태로 존재한다. 그 다음 정현파를 곱해 신호를 passband 신호로 바꾼다.

그 다음 실수부 신호와 허수부 신호를 같은 축으로 보고 서로 더해 최종 신호를 만들게 된다.

신호 $s(t)$를 삼각함수의 덧셈정리를 이용해 결합하면 아래 식과 같다.

위 식을 잘 기억해두자.

QAM 변조의 Constellation Point는 $\sqrt M$-PAM 변조를 직교 형태로 배치한 형태다. 아래 16-QAM의 constellation point를 참고해보자.

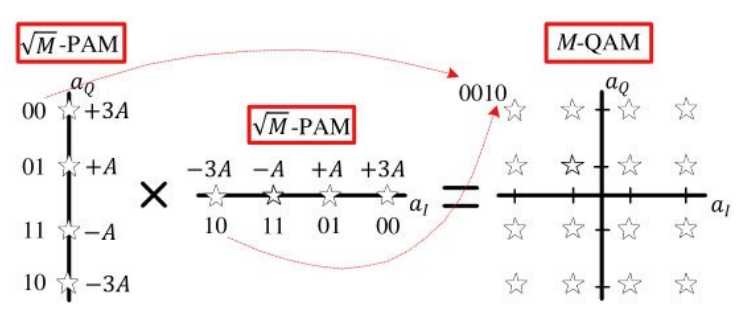
16-QAM은 실수부 4-PAM과 허수부 4-PAM으로 분리 되어 constellation point에 매핑된다.

만약 QAM의 차수가 높아지면 아래 그림과 같아진다.

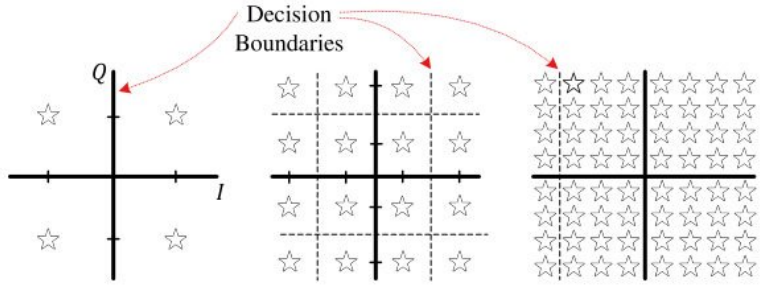
심볼 사이의 constellation point가 가까워 지기 때문에 적은 잡음 전력으로도 심볼 결정 바운더리를 쉽게 넘어설 수 있다.

하나의 심볼에 많은 비트를 압축해 보낼 수 있지만 노이즈에 약해진다는 단점이 있다.

constellation을 통해 평균 심볼 에너지를 도출할 수 있다. 만약 M-QAM의 경우 평균 전력은 아래와 같이 구할 수 있다.

이제 QAM 송신부의 구조를 확인했다. 다음은 QAM 수신부의 구조를 확인해보자. 구조는 아래 그림과 같다.

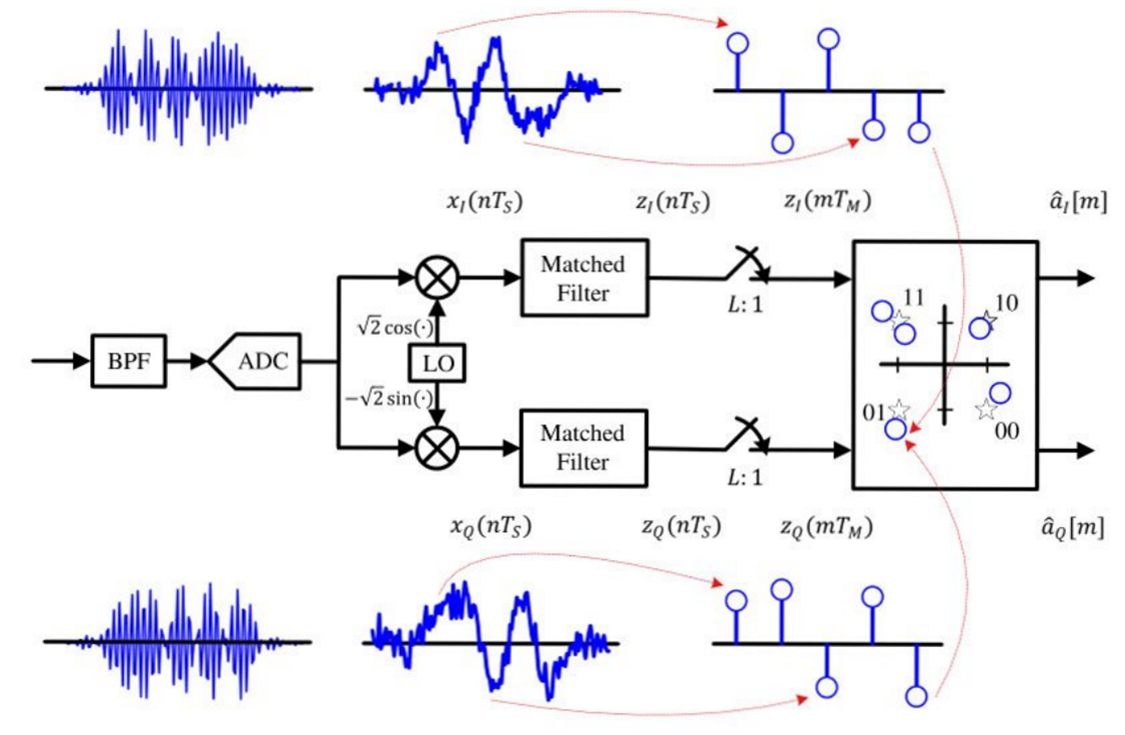
송신부에서 만들어진 신호 $s(nT_S)$는 무선 환경을 거쳐 잡음이 추가 된다. 이 때 잡음은 AWGN만 있다고 가정한다.

아날로그 영역에서 bandpass filter를 통해 upconversion된 passband 신호만을 통과시킨다.

그 다음 ADC를 통해 수신 신호를 디지털 신호로 바꾼다. 이 때 ADC의 샘플링 주기 $T_S$는 DAC의 샘플링 주기와 같다고 가정한다.

그 다음 Local Oscilator에서 정현파 신호를 만들어 실수부 신호와 허수부 신호에 각각 곱해 passband 신호를 baseband신호로 변환한다.

그 다음 Matched Filtering을 수행해 잡음의 크기는 줄이고 신호의 크기는 증폭시킨다.

다음 downsampling을 통해 심볼 위치의 샘플을 추출해 내어 마지막으로 비트로 변환한다.

위 과정을 수학적으로 분석해보자.

만약 노이즈가 없이 수신 신호 $r(t)$는 아래와 같다.

$F_C$는 반송파(carrier)의 주파수에 해당한다. 아날로그 bandpass filter를 통과 시킨 후 ADC를 통과하면 디지털 신호로 바뀐다. 아래 식을 보자.

수신부의 Local Oscilator에서 생성된 정현파 신호를 실수부와 허수부에 각각 곱해주면 아래와 같다.

식을 확인해보면 신호에 반송파 주파수 $F_C$의 2배에 해당하는 항이 존재한다. 이 항은 후에 매치드 필터링을 통해 없어진다.

따라서 매치드 필터링 $z(nT_S)$의 결과는 아래와 같다.

$r_p$는 송신부 pulse shaping filter가 SRRC일 경우 RRC가 된다.

이제 심볼 위치에 해당하는 샘플을 추출하면 아래 식과 같다.

SRRC-Matched Filtering은 심볼 간 간섭이 없기 때문에 $m=0$일 때가 심볼 위치에 해당한다.