4.2 Designing a PLL

4.1 포스팅에서 PLL의 기본 구조를 살펴보았다.

PLL은 무선 통신 모뎀에서 심볼 타이밍 동기화 및 클럭 동기화를 보정하는데 사용된다.

이 때 PLL의 damping factor $\zeta$와 natural frequency $w_n$은 PLL의 특성을 결정 짓는 중요한 파라미터이다.

먼저 Damping factor에 대해 알아보자.

Damping factor는 말 그대로 감쇄 계수이다. 예를 들어 테니스 공을 바닥에 떨어뜨리면 공은 바닥을 치고 다시 튀어 오른다. 시간이 지나면 테니스 공은 더 이상 튀어오르지 않고 평형을 이룬다. 이 때 damping factor는 테니스 공이 얼마나 빨리 평형 상태에 도달하느냐를 결정짓는 파라미터다.

PLL에 대입해서 생각해보면 input 신호의 위상 오차가 얼마나 빨리 수렴되느냐를 결정 짓는 것이 damping factor이다. 아래 그림을 살펴보자.

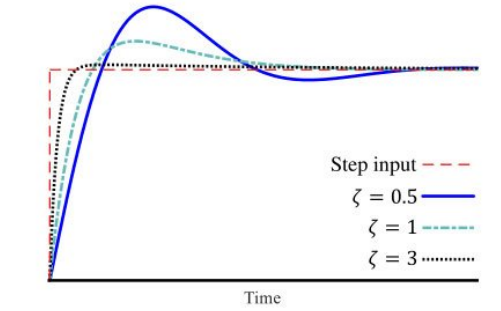
만약 $\zeta$ < 1 일 때는 input 신호에 대해 위로 튀어오르는 overshoot 부분과 아래로 내려가는 undershoot 부분이 보이면서 수렴한다.

이러한 시스템을 underdamped라고 한다.

만약 $\zeta$ > 1 일 때는 overshoot부분이 사라진다. 이러한 시스템을 overdamped 라고 한다.

만약 $\zeta$= 1일 때는 약간의 overshoot를 보이면서 수렴한다. 이러한 시스템을 critically damped라고 한다.

다음으로 Natural frequency에 대해 알아보자.

추후 설명할 예정이지만 평형 상태에 이른 후 정상상태의 PLL은 위상 추적 모드로 동작하고 이 때 PLL은 Low pass filter의 특성을 띤다.

무선 통신에서 수신 신호는 잡음에 의해 왜곡된다.

이 때 PLL은 위상 잡음을 제거해 신호를 복구한다. 이 때 PLL은 loop filter를 통해 시간에 걸쳐 위상 오차 출력을 평균화하고 수렴시키고 NCO를 통해 위상을 조절한다.

따라서 PLL은 위상 잡음은 제거하고 신호를 통과시키는 필터의 역할을 한다. 아래 그림을 보자.

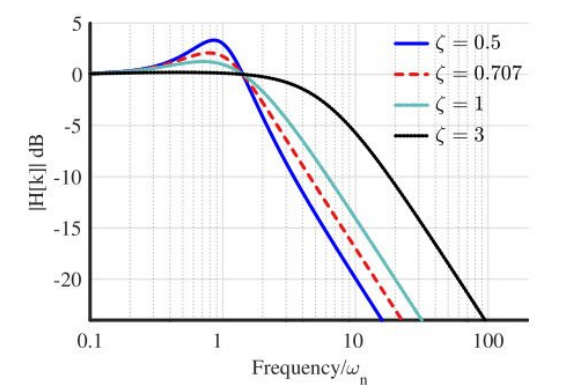
위 그림은 damping factor에 따른 PI를 갖는 PLL의 주파수 응답이다.

그림에서 확인할 수 있듯이 low-pass-filter 모양을 띈다.

또한 low-pass-filter로써 스펙트럼이 $w_n$까지 대략적으로 평탄함을 확인할 수 있다. 이 뜻은 reference 신호의 변동이 $w_n$ 보다 작다면 PLL이 적절히 위상을 추정할 수 있음을 의미한다.

natural frequency $w_n$은 damping factor에 따라 평탄한 정도가 달라진다. 따라서 더 나은 정의를 위해 equivalent noise bandwidth $B_n$을 정의한다.

equivalent noise bandwidth란 총 잡음 전력을 생성하는 이상적인 brick filter의 대역폭으로 정의한다. 아래 그림을 살펴보자.

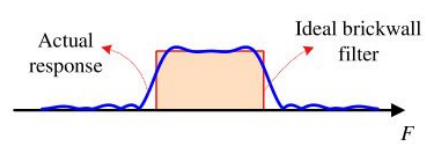
equivalent noise bandwidth는 loop bandwidth라고도 불리며 아래 식으로 결정된다.

PLL을 설계하기 위해서는 먼저 damping factor $\zeta$와 loop bandwidth $B_n$을 정의해야 한다.

damping factor가 클 수록 overshoot는 없지만 더 긴 수렴시간을 긴다. 반대로 damping factor가 작을 수록 빨리 수렴하지만 overshoot가 크다.

일반적으로 damping factor는 $1/\sqrt2$로 설정한다. 또한 유효한 범위는 0.5~2 이다.

작은 loop bandwidth는 대부분의 노이즈를 필터링할 수 있다. 그러나 기준 신호가 $w_n$보다 크게 흔들리면 신호도 필터링 될 위험이 있다.

반대로 큰 loop bandwidth는 기준 신호의 더 큰 움직임도 추적할 수 있으나 더 많은 잡음이 들어오게 된다.

일반적으로 loop bandwidth는 일반적으로 $2\pi/100$의 값을 사용한다.

다음으로 NCO의 이득 $K_0$을 설정해야 한다. 일반적으로 1로 설정한다.

그 다음 phase error detector gain인 $K_D$값을 설정해야 한다. 일반적으로 1로 설정한다.

다음 PI filter의 계수 $K_p$ 와 $K_i$를 설정해야 한다. 일반적으로 아래 식과 같이 설정한다.

위의 식에서 $\theta_n$은 normalized natural frequency 이고 아래 식과 같다.

만약 심볼 당 샘플 수가 $L$인 시스템에서는 $\theta_n$을 전부 $\theta_n/L$로 바꿔서 이득을 설정하면 된다.

이해를 위해 구체적인 예를 통해 PLL이 어떻게 동작하는지 살펴보자.

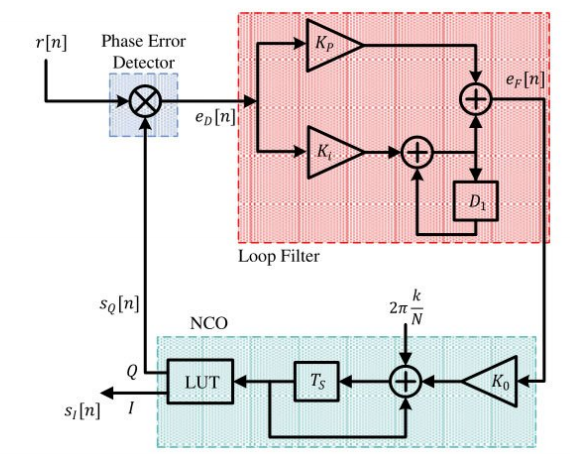
위 PLL 구조에서 input 신호 $r[n]$은 아래와 같다.

$\theta[n]$은 시간에 따라 천천히 변하는 phase이다. PLL은 변하는 phase를 추정하고 보상해야 한다.

우리의 목표는 이 input 신호 $r[n]$의 phase를 $\pi$가 되도록 유지하는 PLL을 설계할 것이다.

입력 신호의 위상은 $\pi$ 근처에서 흔들린다고 가정하자.

먼저 NCO의 output인 $S_I[n]$과 $S_Q[n]$은 아래와 같다.

위 값들은 NCO의 LUT에 저장되어 있다.

이제 phase error detector의 출력 신호인 $e_D[n]$을 살펴보자. 그림에서 수신 신호 $r[n]$과 NCO의 출력 $S_Q[n]$의 곱임을 확인할 수 있다. 아래와 같다.

삼각함수 공식을 활용해 위 식을 변형하면 아래와 같다.

위의 식에서 input 신호의 주파수의 2배에 주파수를 갖는 항이 존재한다.

이 항은 loop filter의 low pass filter 특성에 필터링 된다 따라서 phase error detector의 출력은 아래와 같이 근사화 가능하다.

S-curve 상에서 만약 $\theta_e[n]$이 만약 아주 작다면 비선형 S-Curve를 선형 S-curve로 생각할 수 있다.

따라서 $sinA \approx A$가 성립한다. 그러므로 평균 위상 오차는 아래와 같이 근사화 가능하다.

위 식을 통해 phase error detector의 gain을 유도할 수 있다. 위 식을 잘 보면 위상 오차 $\theta_e$에 $\frac{A}{2}$가 곱해진 형태이므로

phase error detector의 gain은 $K_D= \frac{A}{2}$임을 알 수 있다.

phase error detector의 gain은 $A$값에 따라 달라진다. 그리고 $A$는 PLL 입력 신호의 크기이다.

실제 무선 통신에서는 입력 신호의 크기가 변하므로 phase error detector gain값도 달라져 loop filter가 부정확하게 동작할 위험이 있다.

따라서 PLL로 들어오는 입력 신호는 진폭이 일정해야 한다.

입력 신호의 진폭을 일정하게 만들기 위해서 모뎀 수신부에서는 AGC(Automatic-Gain-Control)을 통해 입력 신호의 진폭을 일정하게 유지시킨다.

AGC를 통과한 입력신호의 진폭이 1로 일정하다고 가정하면 $A=1$된다. 따라서 phase error detector의 gain은 아래와 같이 다시 쓸 수 있다.

다음으로 PLL의 damping factor를 설정할 차례이다. 일반적으로 PLL의 damping factor는 $\zeta = \frac{1}{\sqrt2}$로 설정한다.

PLL의 loop noise bandwidth를 입력 샘플링 주파수의 5%로 설정하면 아래와 같이 설정할 수 있다.

이제 루프 필터의 PI 이득을 설정할 차례이다. 아래의 식에 위의 파라미터를 대입하면 된다.

이제 루프 필터의 PI이득까지 설정을 완료했다.

이제 실제로 PLL의 출력이 어떻게 나오는지 살펴보자.

먼저 phase error detector의 output은 아래와 같다.

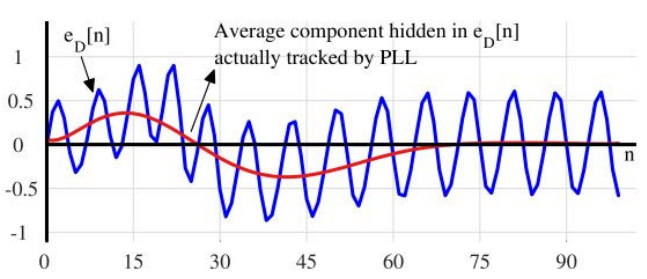
그림의 빨간색 신호는 실제로 PLL의 루프를 거쳐 추정된 위상 오차이다. 70samples 전후로 수렴하는 것을 볼 수 있다.

다음은 loop filter의 출력 신호이다.

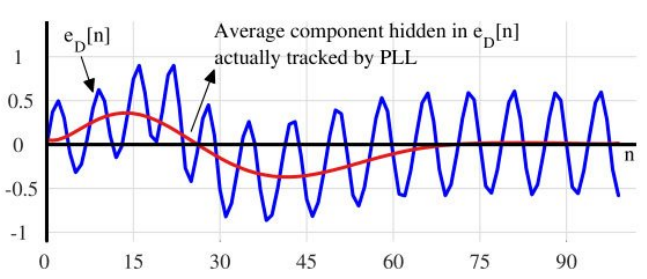
모양은 phase error detector의 출력 $e_D[n]$과 비슷하지만 진폭이 0.5에서 0.15로 감소한 것을 확인할 수 있다.

이러한 감쇄는 PLL의 low pass 특성을 강화시킨다.

마지막으로 NCO에서 phase 추정 결과인 $\hat{\theta[n]}$은 아래 그림과 같다.

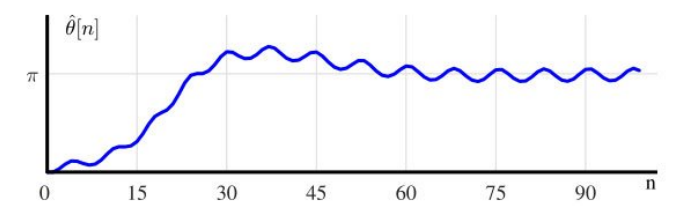
PLL의 목적이 입력신호의 위상을 $\pi$로 수렴시키는 것이었고 이를 달성한 것으로 보인다.

마지막으로 PLL의 출력 신호는 아래 그림과 같다.

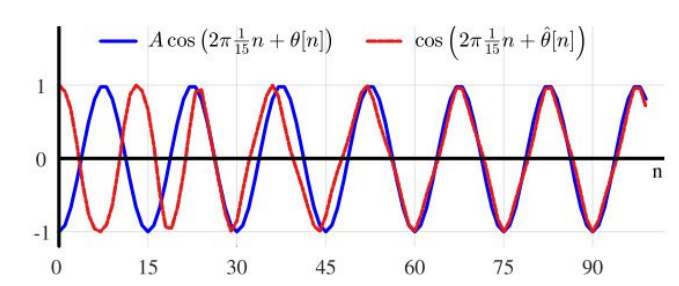
초기 phase 오차는 $\pi$임을 확인할 수 있고 시간이 지나면서 PLL의 출력 신호의 위상이 $\pi$가 되면서 입력신호와 동일한 것을 알 수 있다.