5.1 Feed Forward Carrier Phase Synchornization (Data-Aided)

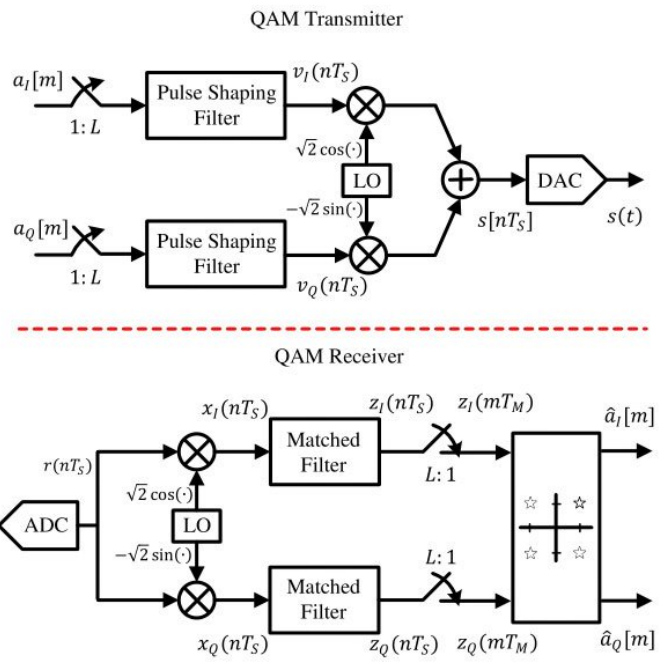
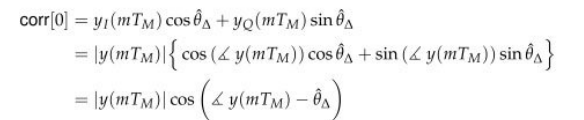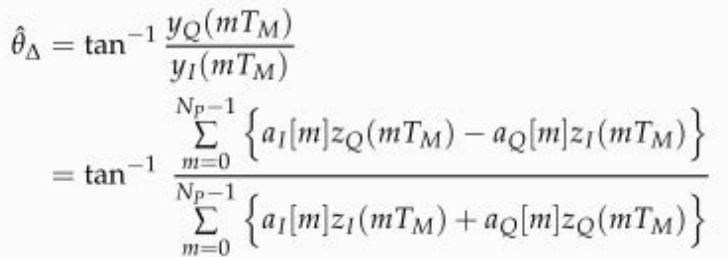앞서 SRRC Pulse Shaping Filter로 생성된 신호는 baseband에 위치한다.

통신을 위해 baseband 신호를 반송파(carrier)와 곱해 passband 신호로 바꿔 준다.

이 때 곱하는 반송파 신호는 정현파 신호이다.

특정 주파수 $f_c$를 갖는 반송파 신호는 송신부의 Local Oscillator에서 생성된다.

수신부로 passband 신호가 수신되고 수신부의 Local Oscillator에서는 동일한 주파수 $f_c$를 생성해 passband 신호를 baseband 신호로 바꿔야 한다.

이 때 송신부의 Local oscillator와 수신부의 Local oscillaotr는 다른 발진기 이기 때문에 정확히 동일한 주파수와 위상을 갖는 정현파를 생성할 수 없다.

이로 인해 수신부에서 baseband로 내린 신호는 주파수 오프셋이 생긴다.

만약 주파수는 동일하다고 가정하면 위상 차이로 인해 발생하는 왜곡을 Carrier Phase offset라고 한다. 아래 그림을 살펴보자.

먼저 DAC 출력으로 나온 신호는 아래와 같이 생성된다. 만약 노이즈가 없고 oscillator에서 주파수는 같고 위상만 다를 경우 수신 신호는 아래와 같다.

위 식에서 $\theta_\triangle$은 ADC와 DAC의 위상 오프셋이다.

송신부에서 Pulse Shaping Filter의 결과 $v_I(nT_S)$와 $v_Q(nT_S)$는 아래와 같다.

Matched Filtering을 통과한 후 심볼 주기에서 샘플을 채취한 신호 $z_I(mT_M)$, $z_Q(mT_M)$은 아래와 같다.

송신부와 수신부의 Oscillator의 주파수 오프셋이 심볼의 위상에 영향을 준다. 아래 그림을 참고해보자.

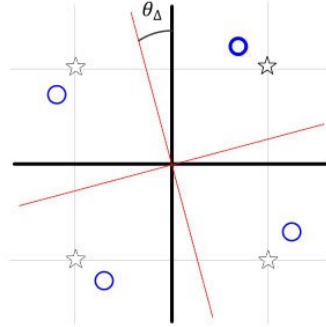
constellation point가 $\theta_\triangle$만큼 반시계 방향으로 회전한 것을 확인할 수 있다.

실제 신호에서 carrier phase offset이 어떻게 발생하는지 확인해보자.

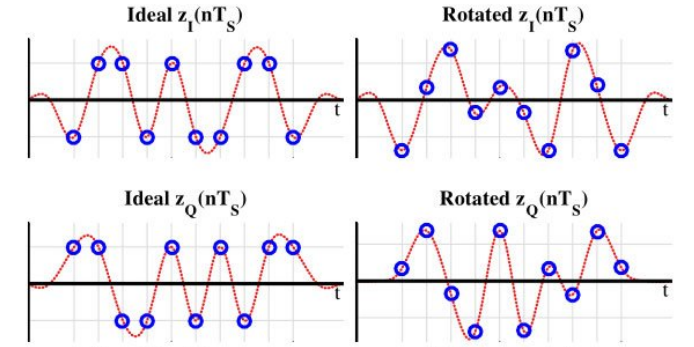
위 그림은 carrier phase offset $\theta_\triangle = 30$도 일 때의 그림이다.

첫 번째 샘플을 비교해보면 Ideal 대비 offset이 발생했을 때 I 심볼과 Q 심볼이 모두 왼쪽으로 이동했음을 확인할 수 있다.

즉 I 심볼의 진폭은 커졌고 Q 심볼의 진폭은 작아졌다.

따라서 carrier phase offset을 보정하는 것은 중요하다. 그러나 여러가지 문제가 있다. 아래 예를 살펴보자.

예를 들기 위해 QAM 변조된 passband 신호를 아래와 같이 나타낼 수 있다.

위 신호는 QAM 변조의 I신호와 Q신호를 합쳐서 표현하기 위해 극형식으로 나타내었다.

식을 살펴보면 신호의 위상은 심볼 $a_Q[m]$과 심볼 $a_I[m]$에 따라 결정된다.

앞선 PLL 포스팅에서 PLL은 점진적으로 변하는 신호의 위상을 추적할 수 있었다.

그러나 심볼의 경우, 만약 BPSK 변조라고 가정하면 위상은 0도 180도로 급변하게 변하기 때문에 PLL의 수렴이 불가하다.

위 그림에서도 알 수 있는건 QAM 변조의 경우 심볼의 위상이 급변하게 변한다. 이러한 급변성은 PLL이 정확하게 동작하지 않는 원인이다.

이를 해결하기 위해서는 신호에서 위상이 급변하는 것을 제거하면 된다.

그 전에 앞서 어떤 상황에서 동기화가 이루어지는지 알아보자.

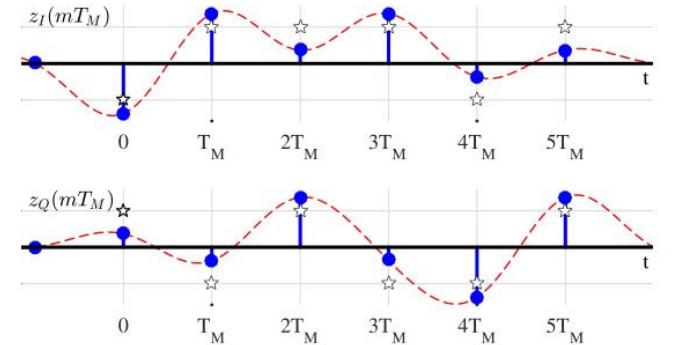
위 그림은 Matched Filtering을 거친 후 정확한 심볼 타이밍에서 추출된 샘플을 나타내었다. 신호에 존재하는 캐리어 위상 offset은 30도로 가정하자.

분명 정확한 심볼 타이밍에 샘플링을 수행했지만 carrier phase offset 때문에 정확한 심볼 위치에서 벗어났다.

우리는 동기화 알고리즘을 사용하여 왜곡된 심볼을 정상적인 심볼 위치에 최대한 가깝게 가져다 놓아야 한다.

앞으로 설명할 carrier phase 동기화 알고리즘은 심볼 속도로 진행되는 알고리즘임을 기억하자.

가장 간단한 방법은 preamble을 이용하는 것이다.

preamble은 송/수신부가 모두 공유하는 정보이므로 수신부도 어떤 심볼이 들어올지 알 수 있다. 따라서 matched filtering을 거쳐 심볼 위치에서 추출된 샘플과

예상되는 심볼의 위상을 비교하면 carrier phase offset을 구할 수 있다. 식으로 나타내면 아래와 같다.

두 번째 방법은 correlation을 사용하는 것이다.

방법은 간단하다. preamble 부분에서 수신부는 carrier phase가 없이 수신된 신호를 안다. 이 신호를 $r(nT_S)$라고 하자.

그리고 실제로 carrier phase offset이 첨가된 신호 $s(nT_s)$가 있다고 가정하자.

여기서 한가지 가정을 하고 넘어가자. 실제로 수신된 신호 $s(nT_s)$는 연속적으로 들어올 것이며 수신부는 알 수 없는 타이밍에 수신된다.

따라서 수신부 입장에서 수신 신호의 시작점이 어디인지를 알아야 한다.

이 때 수신부의 시작점을 결정하는 것을 frame synchronization이라고 한다. 현재는 frame synchronization이 수행 되어 수신 신호의 시작점이 어딘지를

알 수 있다고 가정하자.

이제 correlation 연산을 수행 하면 아래와 같다.

위 식에서 $j$는 수신 신호의 시작점을 의미한다. frame synchronization을 통해 $j=0$일 때 수신 신호의 시작점임을 알았다고 가정하자.

그럼 식은 다시 쓸 수 있다.

여기서 시그마의 $LN_0-1$ correlation을 몇 샘플 수행할지 결정 짓는 파라미터이다.

실제 carrier phase offset을 추정하기 위해 수신된 신호 전체를 correlation을 하면 처리 시간이 오래 걸린다.

따라서 특정 샘플 $LN_0-1$개만 correlation을 수행해 carrier phase offset을 추정한다.

위 식을 풀면 아래와 같다.

여기서 carrier phase offset을 추정해야 하므로 $\theta_\triangle$을 $\hat{\theta_\triangle}$로 바꾸었다.

$cos(A+B) = cosAcosB-sinAsinB$ 공식을 활용하여 위 식을 다시 쓰면 아래와 같다.

그리고 위 식에서 Matched Filtering을 수행 한 후 심볼 인덱스로 식을 표현하면 correlation 식은 아래와 같이 정리 된다.

이제 위 식은 동기화 과정을 유도하는데 계속 나올 테니 기억하자.

이제 correlation을 활용하는 feedforward 방식과 feedback 방식을 알아보자.

먼저 feedforward 방식은 일반적으로 신호가 끊겨 들어오는(Burst 방식) 통신 시스템에 적합하다.

Preamble의 심볼 길이를 $N_P$라고 하면 preamble에 대한 carrier phase noise가 없는 수신 신호와 carrier phase noise가 있는 수신 신호의 correlation은 아래와 같이 표현된다.

위 식에서 식 정리를 위해 아래를 정의하자

따라서 위 식의 실수부와 허수부를 분리하면 아래와 같다.

따라서 correlation식은 아래와 같이 다시 쓸 수 있다.

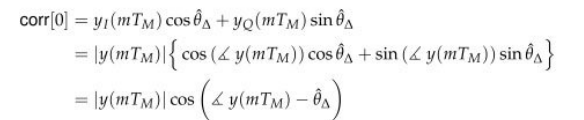
여기서 correlation 결과를 최대로 만드는 $\hat{\theta_\triangle}$이 추정 carrier phase offset이 된다.

즉 cos항이 1이 되면 최대이기 때문에 아래 결과가 도출된다.

그리고 아래처럼 구할 수 있다.

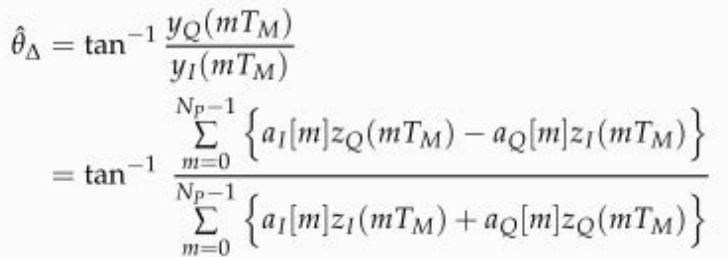
위 식을 이해하기 위해 아래 그림을 참고하자.

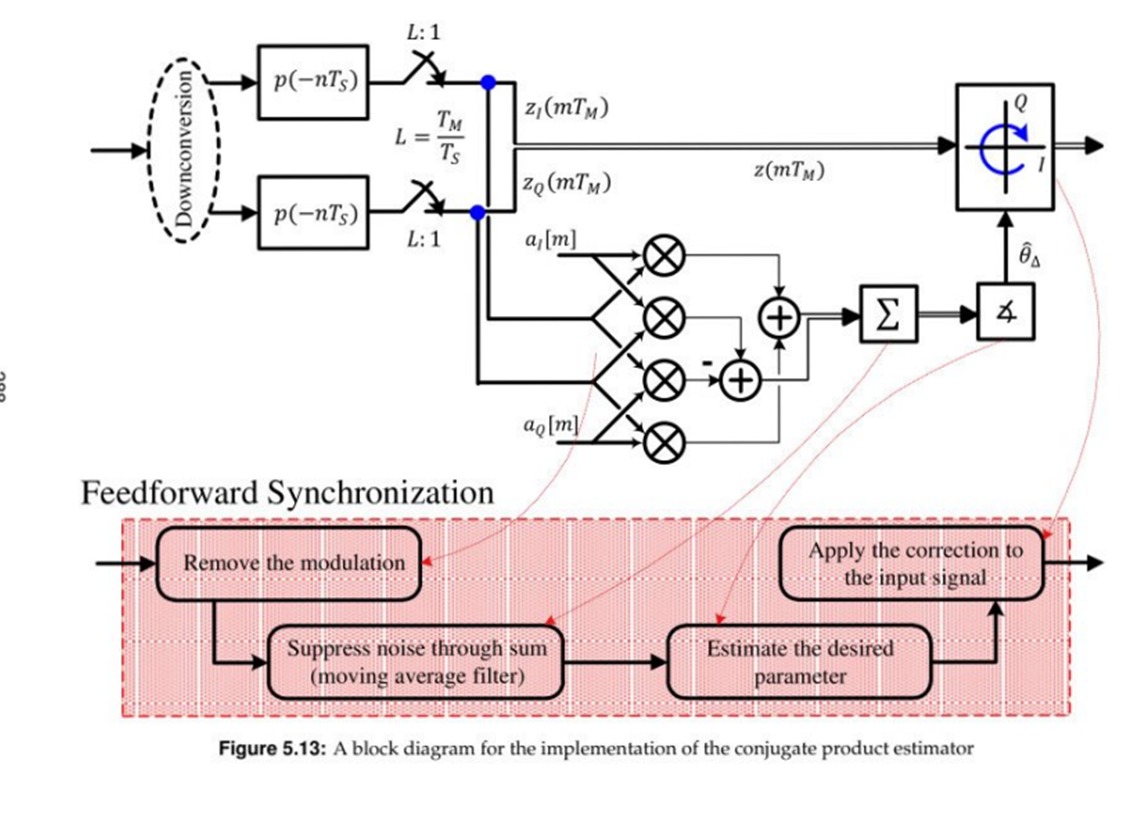
위 결과를 분석해보자.

위 식에서 추정 carrier phase offset을 도출하기 위해 심볼을 conjugate 했다.

conjugate를 수행하면 수신 심볼의 위상이 급변하게 변하는걸 막을 수 있다. 따라서 PLL에 적용 가능하다.

위상에 대한 식을 쓰면 아래와 같다.

즉 원래 심볼 위상이 삭제 되어 carrier phase noise만 남는 것을 확인할 수 있다.

또 carrier phase offset을 구하기 위해 conjugate한 신호의 위상을 누적합 했다.

이를 통해 양수 성분의 노이즈와 음수 성분의 노이즈가 서로 상쇄되어 잡음의 영향을 줄일 수 있다.

아래 그림에서는 carrier phase offset이 도출되는 과정을 시간 축으로 표현했다.

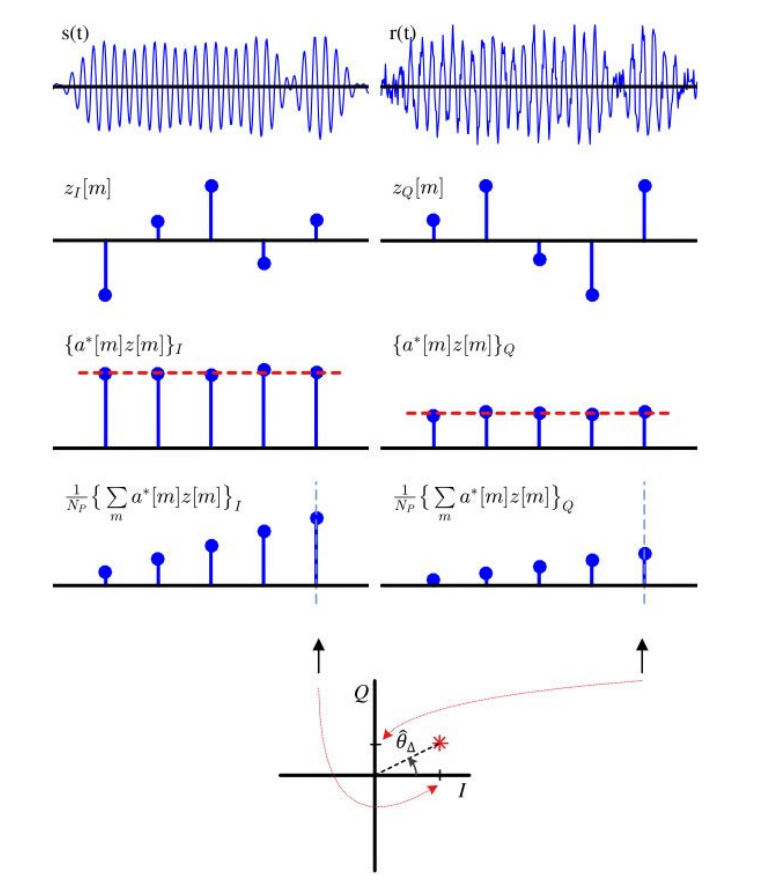
위 추정 과정을 주파수 축에서도 분석할 수 있다.

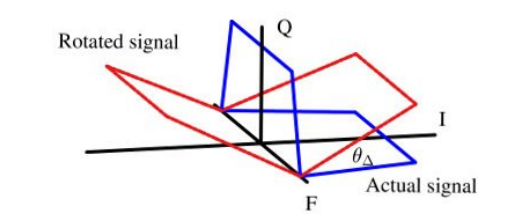
파란색 신호는 carrier phase offset이 없는 스펙트럼이고 빨간색 신호는 carrier phase offset이 있는 신호다.

주파수 축에서 위상이 틀어져 있다.