5.4 Carrier Frequency Offset - 1

송신기와 수신기의 Local Oscillator에서 up conversion과 down conversion을 위한 반송파(carrier)를 생성한다.

이 때 Local Oscillator의 정확도를 ppm term으로 정의할 수 있다.

ppm(parts per million)이란 oscillator가 생성하는 주파수가 기준 값으로 부터 얼마나 벗어났는지를 나타내는 지표이다.

만약 2.4 GHz 주파수를 생성하는 송신부와 수신부의 Oscillator가 $\pm 20$ppm을 갖는다면

송신부와 수신부에서의 각각 생성하는 carrer 주파수의 편차는 아래와 같이 구할 수 있다.

위 주파수 차이는 송신부와 수신부 각각에서 생성하는 주파수 편차를 나타내기 때문에

최악의 경우 48x2=96kHz의 오차가 송수신부 사이에서 발생할 수 있다.

96kHz의 편차가 송수신부의 carrier frequency에 발생하면 신호의 심각한 왜곡을 초래할 수 있다.

더해서 무선 환경을 거치면서 물체가 움직임으로써 발생하는 도플러 쉬프트의 경우

carrier frequency에 수백 Hz의 오차를 추가로 발생시킨다.

비록 도플러 쉬프트는 Oscillator에서 유발하는 편차에 비해 매우 작지만 도플러 쉬프트만으로도 수신 신호 품질에 심각한 영향을 끼친다.

Carrier Frequency Offset(CFO)는 정도에 따라 구분될 수 있다.

먼저 큰 CFO의 경우이다.

송신부와 수신부에서 생성하는 CFO의 차이를 $F_{\Delta,max}$로 나타낸다.

수신부로 들어오는 아날로그 신호는 아날로그 bandpass 필터를 거쳐서 디지털 신호로 바뀐다.

이 때 아날로그 bandpass 필터는 당연하게도 신호의 대역폭 $B$만큼을 평탄하게 통과시켜야 하며 추가로 송신부와 수신부의 최대 CFO만큼을 통과시켜야 한다.

아래 아날로그 필터의 bandpass필터 특성을 나타낸다.

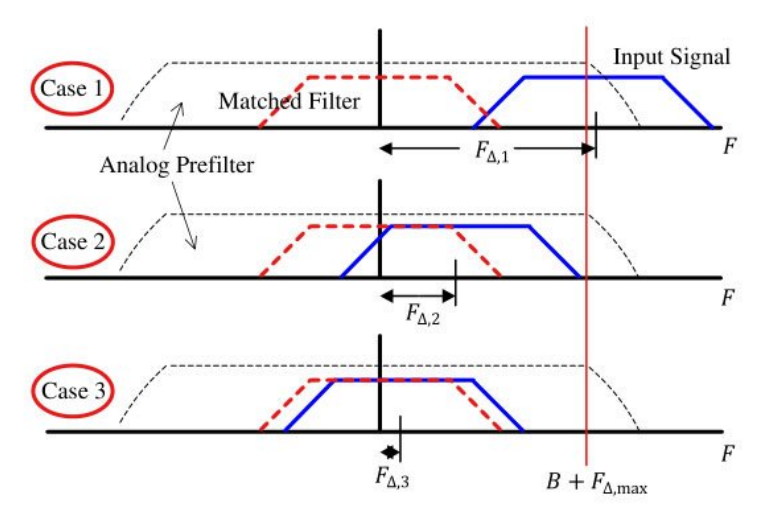
Case 1에서는 수신 신호의 CFO크기가 예상되는 최대 CFO 크기보다 매우 큰 경우다.

따라서 송신 신호는 아날로그 bandpass 필터에 의해 필터링 되어 송신 신호가 없어져 신호 품질에 영향을 준다.

Case 1의 유일한 해결책은 아날로그 bandpass 필터의 통과 대역폭을 여유있게 늘리는 방법 뿐이며 만약 아날로그 단계에서 신호가 필터링 되었다면

디지털 신호처리 영역에서 어떠한 방법으로도 복구할 수 없다.

Case 2에서는 수신 신호의 CFO크기가 예상되는 최대 CFO 크기에 근접하게 큰 경우다.

이 경우 아날로그 필터의 passband 영역에 신호가 모두 위치하기 때문에 Case 1과 달리 신호가 송신 신호가 필터링되지 않는다.

그러나 수신 신호는 반드시 Matched Filtering을 통과해야 한다.

수신 신호에 CFO가 존재한다면 수신 신호의 스펙트럼은 baseband에서 벗어나 있게 되고 baseband에 위치한 Matched Filter와 충분히 겹치지 못한다.

이는 곧 잡음 처리 성능이 줄어 SNR에 영향을 주게 된다. 따라서 CFO는 Matched Filtering 이전에 반드시 추적되고 복구되어야 한다.

Case 3에서는 수신 신호의 CFO크기가 예상되는 최대 CFO 크기에 비해 작은 경우다.

이 경우 수신 신호는 심볼 단위에서는 수신 신호에 큰 영향을 끼치지 않는다. 그리고 Matched Filtering도 정상적으로 동작하게 된다.

따라서 Matched Filtering 및 downsampling 단계를 거쳐 심볼 주기 $T_M$에서 샘플을 선택한 다음 CFO를 복구하게 된다.

이제 CFO의 영향을 확인하기 위해 QAM 모뎀을 예로 든다. 아래 그림을 참고하자.

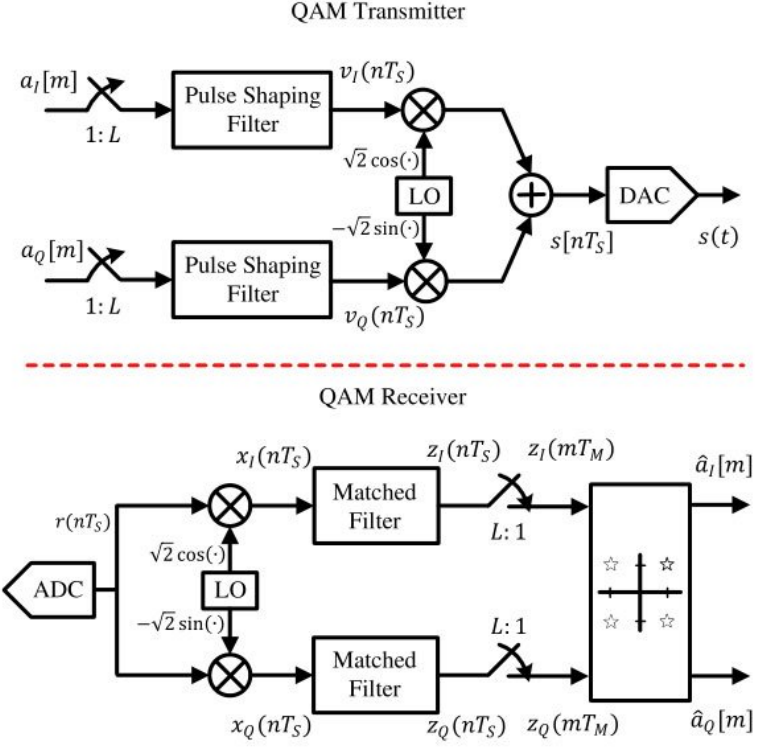
실수부 심볼과 허수부 심볼이 각각 Pulse Shaping을 통과한 신호는 아래와 같이 나타낼 수 있다.

$a_i[i]$와 $a_Q[i]$는 각각 실수부 허수부 심볼이고 $p(nT_S)$는 SRRC Pulse Shaping Filter이다. $T_M$은 심볼 주기 $T_S$는 샘플링 주기 이다.

위 신호는 송신부의 Local Oscillator에서 생성된 각각의 정현파와 곱해져 송신 신호를 만들어 낸다.

노이즈가 없다는 가정에 수신 신호는 아래와 같다.

위 식에서 $F_\Delta$는 수신 신호의 발생한 CFO 이고 $\theta_\triangle$은 CPO(Carrier-Phase-Offset)이다.

Matched Filtering을 거쳐 심볼 주기에서 선택된 신호는 아래와 같다.

위 경우는 CFO가 작은 경우에 해당한다. 따라서 CFO 보정없이 Matched Filtering을 통과한 경우다.

위 식에서 $F_0$는 Normalized CFO(nCFO) 이다. nCFO는 아래와 같이 구할 수 있다.

$R_M$은 Symbol Rate이고 $T_M$은 심볼 주기 이다.

이제 $z_I(mT_M)$과 $z_Q(mT_M)$을 극 형식으로 나타내면 아래와 같다.

위 식을 잘 보면 $F_0$는 신호의 크기는 변화시키지 않지만 위상을 변화 시킨다.

$2\pi F_0m$ 항은 $m$이 바뀔 때마다 크기가 변하기 때문에 위상이 변하는 것이다. 이 효과를 Constellation point로 확인해보자.

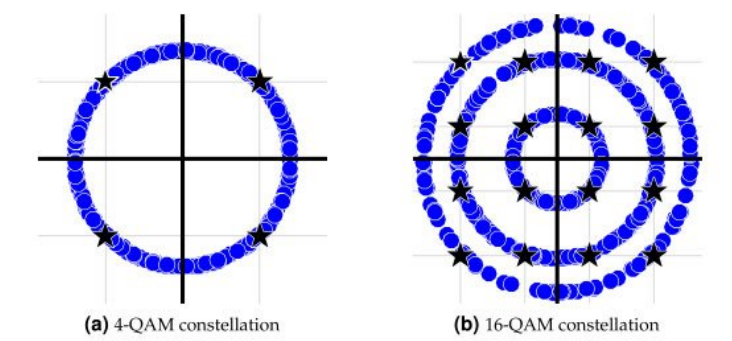
위 그림에서 확인할 수 있듯이 Constellation point가 회전하는 것을 볼 수 있다.