5.3 Feedback Carrier Phase Synchronization -2 (Data aided)

앞선 5.2 포스팅에서 소개된 carrier phase synchronization은 phase error detector에서 매치드 필터링 출력의 실수부와 허수부의 위상을 통해
phase offset을 추정했다.

이 때 phase offset을 구하기 위해서 역탄젠트 함수를 사용했다.

실제 역탄젠트를 하드웨어로 구현하기 위해서는 크게 3가지 방법을 사용한다.

크게 Cordic, Polynomial Approximation, Look up table이 그 예시이다. 여기서 이 3가지 알고리즘에 대한 자세한 방법은 다루지 않는다.

위에 기술된 3가지 알고리즘은 하드웨어 면적을 많이 차지한다. 따라서 면적 측면에서 구현에 비합리적인 요소가 존재한다.

이를 해결하기 위해서 역탄젠트를 사용하지 않고 carrier phase offset을 추정할 수 있는 phase error detector가 고안되었다.

그것은 바로 벡터곱을 이용한 cross product phase error detector 이다.

우리는 correlation을 통한 feedforward carrier phase synchronization 기법을 앞서 살펴보았다. 식을 다시 쓰면 아래와 같다.

원리를 다시 살펴보면 preamble 신호와 실제 수신된 신호의 correlation값을 가장 크게 만드는 $\hat{\theta_\triangle}$이 phase offset 이었다.

즉 핵심은 correlation의 결과를 최대로 만드는 $\hat{\theta_\triangle}$을 찾는 것이다.

여기서 우리는 미분을 생각할 수 있다. 미분 값을 0으로 만드는 $\hat{\theta_\triangle}$는 그 지점에서 최댓값을 가진다.

위 식을 $\hat{\theta_\triangle}$에 대해 미분하면 아래와 같다.

이때 위 식을 0으로 만드는 $\hat{\theta_\triangle}$이 바로 correlation을 최대로 만드는 값, 즉 추정 phase offset 이다.

$\theta$만큼 시계 방향하는 회전 변환은 $Icos\theta+Qsin\theta$ 와 $Qcos\theta-Isin\theta$와 같다.

따라서 매치드 필터를 $\theta$만큼 시계 방향으로 회전하는 변환은 아래와 같이 쓸 수 있다.

위 식을 미분식에 대입하면

위 식을 최대로 만드는 조건은 아래와 같다.

즉 phase error detector의 출력 $e_D[m]$은 아래와 같다.

자 이제 feedback cross product carrier phase synchronizer 와 feedforward carrier phase synchronizer의 phase error detector 를 비교해보자.

위 식에서 첫 번째 식은 feedback cross product synchronizer의 phase error detector 출력을 나타낸 것이다.

위 식에서 두 번째와 세 번째 식은 feedforward synchronizer의 역탄젠트로 위상을 추정할 실수부와 허수부 이다.

식을 잘 살펴보면 feedforward synchronizer의 허수부와 feedback cross product synchronizer가 비슷한 형태를 띄고 있음을 확인할 수 있다.

한 가지 차이점은 $z_I(mT_M)_{sync}$냐 $z_I(mT_M)$이냐의 차이다.

여기서 feed back cross product synchronizer의 미분값이 0일 때 phase offset이 추정된다.

비슷하게 위 식의 세 번째 식(feedforward synchronizer의 허수부)가 0으로 가면 위 식의 두 번째 식(feedforward syncrhonizer의 실수부)이 최대로 갈 것이다.

무슨 뜻이냐면 복소평면에서 단위원을 그리는 실수부 벡터 $I$와 허수부 벡터 $Q$가 있는데 허수부 벡터 $Q$가 0으로 가면 자연스럽게 실수부 벡터 $I$가 최대로 가는 것과 같다.

만약 $z_I(mT_M)$ 대신 $z_I(mT_M)_{sync}$를 사용한다고 가정해보자.

이는 곧 feedback cross product synchronizer가 허수부 성분을 0으로 만드는 방식으로 동작함을 생각할 수 있다.

이제 feedback cross product synchronizer의 S-curve에 대해 살펴보자.

먼저 feedforward synchronizer는 수신 신호의 실수부와 허수부 성분의 위상을 토대로 phase offset을 추정했다.

따라서 수신 신호의 크기 $A$는 고려 대상이 아니었다.

그러나 feedback cross product synchronizer는 이야기가 다르다.

위의 식 처럼 feedback 구조의 phase error detector의 출력은 수신 신호의 크기 $a_I[m]$과 $a_Q[m]$에 직접적으로 영향을 받는다.

따라서 자세한 유도는 생략하지만 feedback 구조의 평균 phase error detector 오차 $\bar{e_D}$에는 수신 신호의 크기 성분 $A$가 필요하다.

따라서 아래 식처럼 표현 가능하다.

그리고 위 식을 토대로 S-curve를 그리면 아래와 같다.

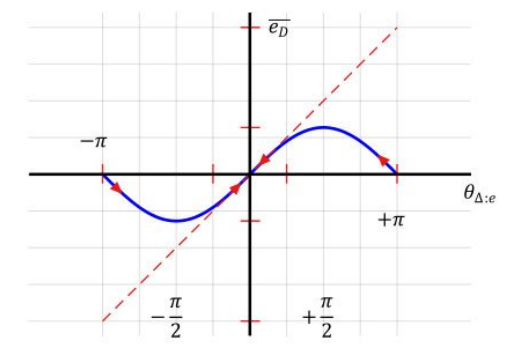
그림을 살펴보면 $[-\pi/4 \ \ \ \pi/4]$ 영역에서 S-curve는 거의 선형적인 특성을 갖는다.

또한 $\theta_{\triangle:e}$가 0 근처에서만 양수 기울기를 갖기 때문에 최종 lock phase에 대한 모호성이 없다.

위 그림에서 점선으로 표시된 선은 역탄젠트 기반 feedback 구조의 S-curve 특성이었다.

두 S-Curve 특성을 분석해보자.

cross product feedback 구조는 $\theta_{\triangle:e}$가 클 때 즉 위상 오차가 많이 날 때 역탄젠트 기반 feedback 구조와 달리 S-Curve의 기울기가 완만하다.

기울기가 완만하다는 것은 큰 위상 오차가 발생했을 때 왜곡하려는 힘이 적다는 뜻이다.

즉 cross product feedback 구조의 S-curve가 역탄젠트 기반 feedback구조에 비해 큰 위상 오차에 강인하다는 뜻이다.