트리 (Tree)

트리 (Tree) 란?

트리 Tree는 데이터 구조 중 하나로, 계층적으로 구성된 노드들의 집합을 나타낸다. 트리는 하나의 루트 노드(root node)에서 시작해서 여러 개의 자식 노드(child node)를 가지며, 자식 노드들도 각각 다시 자신의 자식 노드들을 가질 수 있다.

트리는 데이터를 계층적으로 구성하고 관리하는 데 매우 유용한 자료구조이다.
예를 들어, 조직도, 가계도 및 파일 시스템에서 폴더 구조(디렉터리)와 파일들의 관계를 나타내는 데 사용되고, 알고리즘에서도 널리 활용되는데 대표적인 예로는 이진 탐색(Binary Search)이 있다.

---

트리 용어

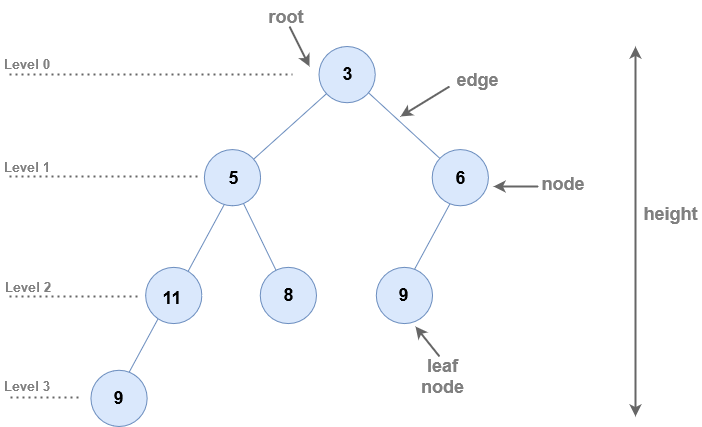
• 노드(node) : 트리 구조의 자료 값을 담고 있는 단위
• 루트(root) : 트리의 맨 위에 있는 노드
• 리프(leaf) : 자식 노드가 없는 노드
• 인터널(internal) : 리프 노드를 제외한 모든 노드
• 엣지(edge) : 노드 간의 연결선 (=link, branch)
• 부모(parent) : 자식 노드를 가지는 노드
• 자식(child) : 부모 노드로부터 연결된 하위 노드
• 형제(sibling) : 같은 부모를 가지는 노드
• 깊이(depth) : 루트 노드로부터 얼마나 멀리 있는지 나타내는 수치
• 높이(height) : 하위 노드 중 가장 멀리 떨어진 잎 노드까지의 깊이
• 크기(size) : 자신을 포함한 자식 노드의 개수
• 차수(degree) : 각 노드가 지닌 가지(엣지)의 수
• 트리의 차수 : 트리의 최대 차수

---

트리의 특징

1. 하나의 노드에서 다른 노드로 이동하는 경로는 하나뿐
2. 노드가 n개인 트리의 edge의 수는 n-1개
3. Acyclic(Cycle싸이클이 존재하지 않음)
4. 모든 노드는 서로 연결되어 있음
5. 하나의 Edge를 끊으면 2개의 Sub-Tree로 분리됨

---

이진 트리 (Binary Tree)란?

이진 트리(binary tree)는 각 노드가 최대 두 개의 자식 노드를 가지는 트리 구조이다.
자식 노드는 왼쪽 자식과 오른쪽 자식을 구분한다. (순서 트리)
아래 두 트리는 서로 다른 트리이다.

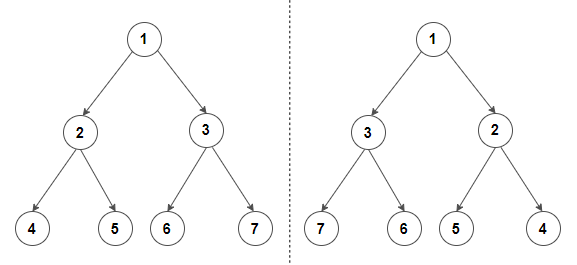
이진 트리는 매우 중요한 자료 구조 중 하나이며, 다양한 알고리즘에서 사용된다. 이진 탐색 트리(binary search tree)는 이진 트리의 일종으로, 특히 검색과 삽입 연산에서 매우 효율적인 구현이 가능하다.

이진 트리는 매우 다양한 변형이 있으며, 이진 탐색 트리 외에도 AVL 트리, 레드-블랙 트리, B-트리 등 많은 유형이 있습니다. 각각의 트리는 다른 목적을 가지고 있으며, 특정한 알고리즘에서 더욱 효율적인 구현을 가능하게 합니다.

1. 이진트리의 종류

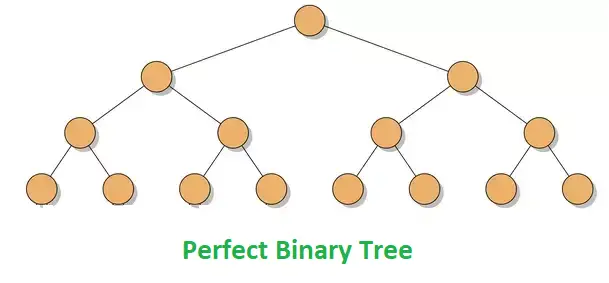
포화 이진 트리

• 모든 레벨에서 노드들이 꽉 채워져 있는 트리 (Perfect Binary Tree)
  

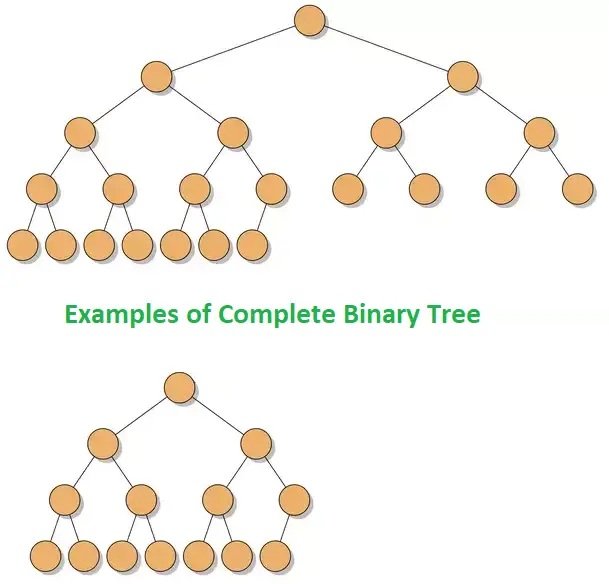
완전 이진 트리

• 마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리 (Complete Binary Tree)
  단, 마지막 레벨은 좌측이 채워져있어야 한다.
  

정 이진 트리

• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리 (Full Binary Tree)
  

편향 트리

• 한쪽으로 기울어진 트리, 사향 트리라고도 한다. (Skewed Binary Tree)
• 옆으로 눕히면 연결리스트와 똑같은 형식이다 (연결리스트도 트리의 일종임)
  

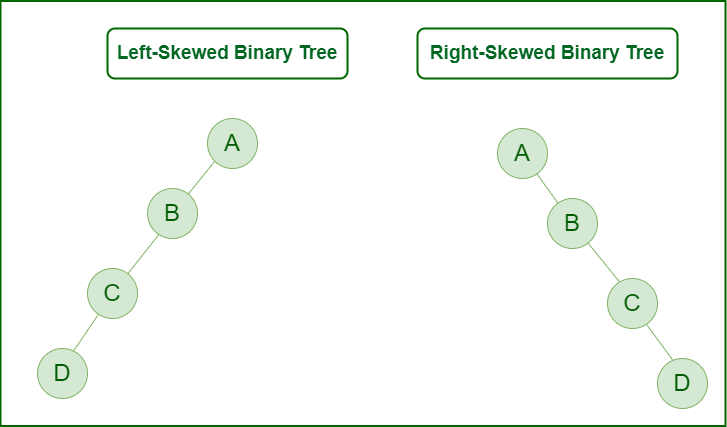
균형 이진 트리

• 모든 노드의 좌우 서브 트리 높이가 1레벨이상 차이나지 않는 트리 (Balanced Binary Tree)
  

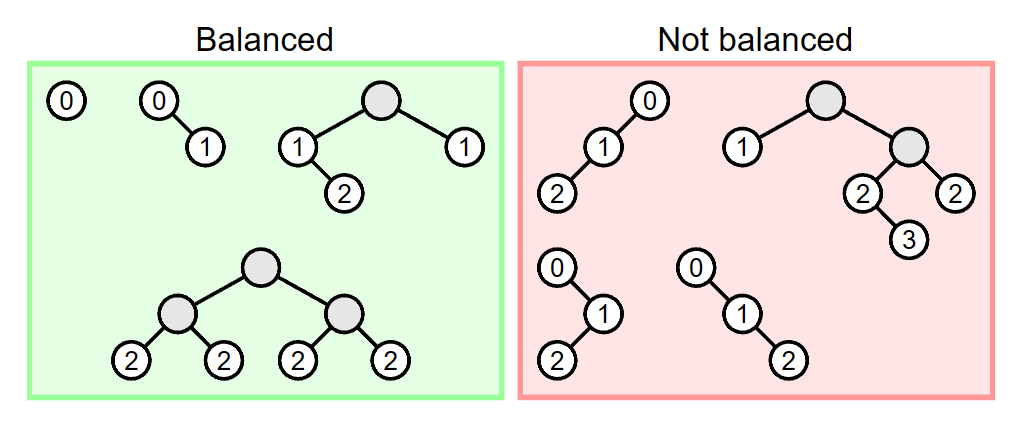
2. 이진 트리의 특징

• 포화 이진 트리의 높이가 h일 때, 노드의 수는 2의 h+1승-1개이다.
  1개의 부모 노드와 2개의 자식 노드를 가진 트리를 예로 들면,
  높이는 1이고 2의 1+1승 -1이니, 4-1= 3이 나온다.
• 포화(or 완전) 이진 트리의 노드가 n개일 때, 높이는 logN (소수점 버림)
  1개의 부모 노드와 2개의 자식 노드를 가진 트리를 예로 들면,
  부모 1개 자식 2개인 트리이기 때문에, log3(밑은 2)이 되고, 1.---이 나오기 때문에
  소숫점을 버리면 1이 나온다. 즉 높이는 1이다.
• 이진 트리의 노드가 n개일 때, 최대 가능 높이는 n-1
  (0부터 시작하니 -1을 넣는 것임 / 편향 트리일 경우가 최대)

3. 이진 트리의 순회

• 모든 노드를 빠트리거나 중복하지 않고 방문하는 연산
• 순회 종류는 4가지
  a. 전위 순회, 중위 순회, 후위 순회 (DFS)
  b. 레벨 순회 (BFS)

1. 전위순회 (Pre-order Traversal)
   전위순회는 트리의 구조를 파악하기 위해 사용될 수 있고, 트리의 노드를 복사하거나 클론하는 경우에 유용하다.

2. 중위순회 (In-order Traversal)
   중위순회는 정렬된 값을 출력하거나, 특정한 노드를 찾는 등의 작업에 사용될 수 있다.

3. 후위순회 (Post-order Traversal)
   후위순회는 트리의 리프 노드에서 시작해서 루트 노드로 탐색하는 것과 같은 방법으로 사용될 수 있고,
   후위순회를 이용하면 트리의 노드를 삭제하는 경우에 유용합니다.

4. 레벨순회 (Level-order Traversal)
   트리의 레벨별로 작업을 수행해야 할 때 사용된다.

전위 순회 (Preorder Traversal)

방문순서 : 현재 노드 ▶ 왼쪽 노드 ▶ 오른쪽 노드

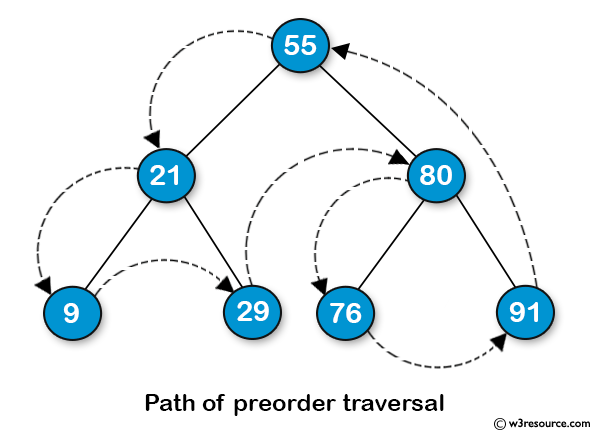
중위 순회 (Inorder Traversal)

방문순서 : 왼쪽 노드 ▶ 현재 노드 ▶ 오른쪽 노드

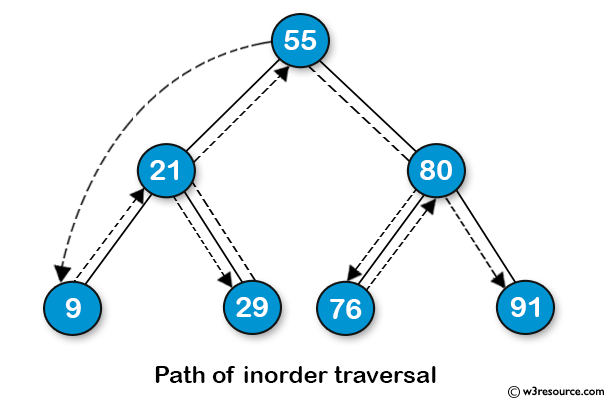
후위 순회 (Postorder Traversal)

방문순서 : 왼쪽 노드 ▶ 오른쪽 노드 ▶ 현재 노드

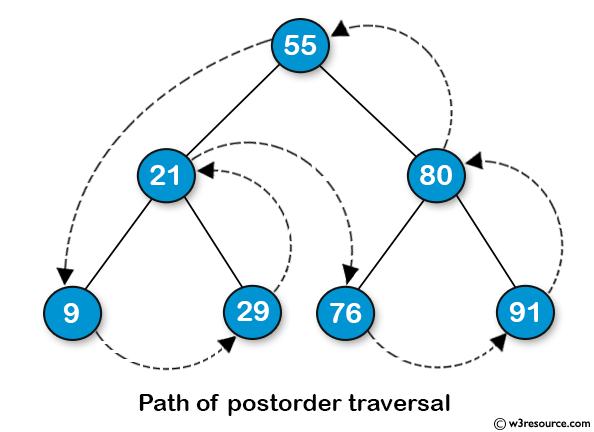
레벨 순회 (Levelorder Traversal)

방문순서 : 위쪽 레벨부터 왼쪽 노드 ▶ 오른쪽 노드

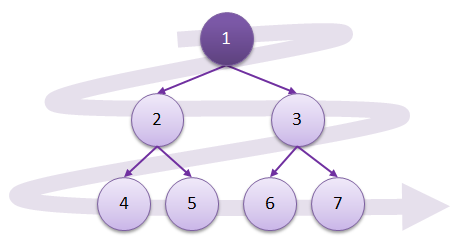
4. 이진 트리 구현

이진 트리를 구현하는 방법에는 두 가지가 있다.
하나는 배열(array)을 사용하는 방법이며, 다른 하나는 연결 리스트(linked list)를 사용하는 방법이다.

• 배열 사용
  이진 트리를 배열로 구현하는 방법은, 루트 노드부터 시작하여 왼쪽 자식 노드는 현재 노드의 인덱스에 2를 곱한 값, 오른쪽 자식 노드는 현재 노드의 인덱스에 2를 곱한 값에 1을 더한 값으로 저장하는 방법이다. 따라서 배열 인덱스 0은 루트 노드를 가리키게 된다.
  배열을 사용하는 이진 트리 구현 방법은 노드의 추가나 삭제가 일어날 때 배열의 크기를 동적으로 변경해야 하는 단점이 있다. 따라서 배열을 사용하는 방법은 이진 트리의 크기가 미리 결정되어 있는 경우에 사용하는 것이 적합하다.

• 연결 리스트 사용
  이진 트리를 연결 리스트로 구현하는 방법은, 각 노드가 데이터와 왼쪽, 오른쪽 자식 노드를 가리키는 포인터를 가지도록 구현하는 방법이다. 각 노드는 동적으로 할당되며, 노드의 추가나 삭제가 용이하다.
  연결 리스트를 사용하는 이진 트리 구현 방법은 동적 메모리 할당과 포인터 연산이 필요하므로 배열을 사용하는 것보다 일반적으로 느릴 수 있다. 그러나 노드의 추가나 삭제가 빈번하게 일어나는 경우에는 연결 리스트를 사용하는 것이 더욱 효율적이다.

---

예제 소스코드 1

백준 - 트리의 부모 찾기

import java.util.*;

public class Main {
    static int N;
    static ArrayList<Integer>[] adj;
    static int[] parent;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        N = sc.nextInt();

        // 인접 리스트 생성
        adj = new ArrayList[N + 1];
        for (int i = 1; i <= N; i++) {
            adj[i] = new ArrayList<>();
        }

        // 노드 연결 정보 입력
        for (int i = 0; i < N - 1; i++) {
            int u = sc.nextInt();
            int v = sc.nextInt();

            // 무향 그래프이므로 양방향으로 연결
            adj[u].add(v);
            adj[v].add(u);
        }

        parent = new int[N + 1];
        dfs(1, 0);

        // 루트 노드를 제외하고 각 노드의 부모 노드 출력
        for (int i = 2; i <= N; i++) {
            System.out.println(parent[i]);
        }

        sc.close();
    }

    // DFS를 이용하여 각 노드의 부모 노드를 찾는 함수
    private static void dfs(int cur, int prev) {
        parent[cur] = prev;

        for (int next : adj[cur]) {
            if (next != prev) {
                dfs(next, cur);
            }
        }
    }
}

위의 코드에서는 인접 리스트를 이용하여 트리를 구성하고, DFS(Depth-First Search) 알고리즘을 이용하여 각 노드의 부모 노드를 찾는다.

먼저, N 변수에 노드의 개수를 입력받고, adj 변수에는 인접 리스트를 생성한다. 이후, 입력받은 노드 연결 정보를 이용하여 무향 그래프를 생성하고, 무향 그래프이므로 각 연결 정보에 대해 양방향으로 연결한다.

그 다음으로는 parent 배열을 초기화하고, DFS를 이용하여 각 노드의 부모 노드를 찾는다.
DFS 함수에서는 현재 노드의 부모 노드를 저장하고, 자식 노드를 탐색한다.
자식 노드는 부모 노드와 연결된 노드이며, 이미 방문한 노드인 경우에는 탐색하지 않는다.

마지막으로는 루트 노드를 제외하고, 각 노드의 부모 노드를 출력한다.

---

예제 소스코드 2

백준 - 이진 검색 트리 (5639)

import java.util.Scanner;

class Node {
    int data;
    Node left;
    Node right;

    public Node(int data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

public class Main {
    static Node root = null;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int data = sc.nextInt();
        root = new Node(data);

        while (sc.hasNext()) {
            data = sc.nextInt();
            insert(root, data);
        }

        postorder(root);
    }

    // 이진검색트리에 노드를 삽입하는 함수
    private static void insert(Node node, int data) {
        if (data < node.data) {
            if (node.left == null) {
                node.left = new Node(data);
            } else {
                insert(node.left, data);
            }
        } else {
            if (node.right == null) {
                node.right = new Node(data);
            } else {
                insert(node.right, data);
            }
        }
    }

    // 후위순회(postorder) : 왼쪽 자식 -> 오른쪽 자식 -> 루트
    private static void postorder(Node node) {
        if (node == null) {
            return;
        }

        postorder(node.left);
        postorder(node.right);
        System.out.println(node.data);
    }
}

위의 코드에서는 Node 클래스를 정의하여 이진트리를 구현한다. 이진검색트리에 노드를 삽입하는 insert 함수와 후위순회를 수행하는 함수 postorder를 구현하였다. 이진검색트리의 루트 노드를 root 변수에 저장하고, 전위순회 결과를 입력으로 받아서 이진검색트리를 생성한다. 이진검색트리에서는 노드를 삽입할 때, 현재 노드보다 작은 값은 왼쪽 자식 노드에, 큰 값은 오른쪽 자식 노드에 삽입한다. 이렇게 생성된 이진검색트리를 후위순회한 결과를 출력한다.