이진 탐색 트리 (Binary Search Tree)
AVL트리BFBSTBalance FactorBinarySearchTreeINSERTREDBLACK트리RLRRRed-blackavlbalancedbinaryblackinsertFixuplllrredsearchtree검색균형균형이진탐색트리균형이진트리기본코드노드단순회전리밸런싱부모불균형삭제삽입서브트리시간복잡도이중회전이진자식추가코드탐색트리특징편향회전
0
자료구조
목록 보기
12/14
이진 트리와 이진 탐색 트리(BST)의 차이
이진 트리(Binary Tree)와 이진 탐색 트리(Binary Search Tree, BST)는 트리(Tree) 자료구조의 일종으로, 노드(Node)들이 서로 연결된 구조를 가지고 있다. 이 둘은 매우 비슷한 구조를 가지고 있지만, 한 가지 중요한 차이점이 있다.
이진 트리는 각 노드가 최대 두 개의 자식 노드를 가지는 트리다. 이진 트리의 모양은 매우 다양하며, 트리의 높이가 균등하지 않을 수 있다. 이진 트리에서는 특별한 규칙이 적용되지 않는다.
반면, 이진 탐색 트리는 이진 트리의 일종으로, 각 노드가 최대 두 개의 자식 노드를 가지며, 다음과 같은 조건을 만족한다.
- 왼쪽 서브트리에 있는 모든 노드의 값은 해당 노드의 값보다 작다.
- 오른쪽 서브트리에 있는 모든 노드의 값은 해당 노드의 값보다 크다.
즉, 이진 탐색 트리는 모든 노드가 서로 다른 값을 가지며, 왼쪽 서브트리에 있는 모든 노드는 해당 노드보다 작은 값을 가지며, 오른쪽 서브트리에 있는 모든 노드는 해당 노드보다 큰 값을 가지도록 구성된다. 이진 탐색 트리에서는 값을 검색할 때, 이러한 성질을 이용하여 효율적으로 검색할 수 있다.
이진 트리와 이진 탐색 트리는 모양이 비슷하지만,
이진 탐색 트리는 값을 저장하고 검색하는 데 효율적입니다.
따라서, 값을 검색하는 기능이 필요한 경우에는 이진 탐색 트리를 사용하는 것이 좋습니다.
이진 탐색 트리의 시간복잡도
- 균형 상태 :
O(logN) - 불균형 상태 :
O(N)(ex. 사향트리)
이진 탐색 트리 - 탐색
이진 탐색 트리에서 특정 값을 찾기 위해서는 다음과 같은 순서로 탐색한다.
- 루트 노드부터 시작
- 찾으려는 값이 현재 노드의 값과 일치하면 탐색을 종료
- 찾으려는 값이 현재 노드의 값보다 작으면 현재 노드의 왼쪽 자식 노드로 이동
- 찾으려는 값이 현재 노드의 값보다 크면 현재 노드의 오른쪽 자식 노드로 이동
- 찾으려는 값이 트리에 없는 경우, null 반환
- 어떤 데이터를 찾더라도 최대 트리 높이 만큼의 탐색이 이루어짐
이진 탐색 트리 - 삽입(추가)
이진 탐색 트리에서 새로운 값을 삽입하는 과정은 다음과 같다.
- 루트 노드부터 시작
(중복 key 발견 시 노드 추가하지 않고 종료) - 삽입하려는 값이 루트 노드보다 작으면 왼쪽으로 이동
- 삽입하려는 값이 루트 노드보다 크면 오른쪽으로 이동합니다.
- leaf노드 도달 후, key를 비교하여 작으면 왼쪽, 크면 오른쪽에 삽입
위 과정을 반복하여 새로운 값을 삽입하면, 이진 탐색 트리가 계속해서 정렬된 상태를 유지하면서 데이터를 저장할 수 있다.
이진 탐색 트리 - 삭제
이진 탐색 트리에서 값을 삭제하는 과정은 다음과 같다.
- 삭제할 노드가 자식 노드가 없는 노드인 경우, 그냥 삭제한다.
(이 경우 삭제하려는 노드의 부모의 연결링크를 null값으로 바꾼다)
- 삭제할 노드가 자식 노드를 1개 가지고 있는 경우, 삭제할 노드의 부모 노드와 삭제할 노드의 자식 노드를 연결한다.
- 삭제할 노드가 자식 노드를 2개 가지고 있는 경우,
a. 왼쪽 서브트리에서 가장 큰 값을 가진 노드나or
b. 오른쪽 서브트리에서 가장 작은 값을 가진 노드를
삭제하려는 위치로 가져오고, 엣지 연결 작업을 새로해준다.
새로 가져온 값이 기존에 있었던 자리의 가지도 값을 재정리해준다.
이진 탐색 트리 기본 소스코드
// 이진 탐색 트리의 노드 클래스
class Node {
int key; // 노드가 가지는 값
Node left;
Node right; // 왼쪽과 오른쪽 자식 노드
// 생성자
public Node(int item) {
key = item;
left = null;
right = null;
}
}
// 이진 탐색 트리 클래스
class BinarySearchTree {
Node root; // 이진 탐색 트리의 루트 노드
// 생성자
BinarySearchTree() {
root = null;
}
// 이진 탐색 트리에 새로운 노드를 삽입하는 메서드
public void insert(int key) {
root = insertNode(root, key);
}
// 이진 탐색 트리에서 노드를 삽입하는 내부 메서드
public Node insertNode(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key)
root.left = insertNode(root.left, key);
else if (key > root.key)
root.right = insertNode(root.right, key);
return root;
}
// 이진 탐색 트리에서 노드를 삭제하는 메서드
public void delete(int key) {
root = deleteNode(root, key);
}
// 이진 탐색 트리에서 노드를 삭제하는 내부 메서드
public Node deleteNode(Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode(root.left, key);
else if (key > root.key)
root.right = deleteNode(root.right, key);
else {
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
root.key = minValue(root.right);
root.right = deleteNode(root.right, root.key);
}
return root;
}
// 주어진 노드에서 최소값을 반환하는 메서드
public int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
}
return minv;
}
// 중위 순회를 수행하여 이진 탐색 트리를 출력하는 메서드
public void inorderTraversal(Node root) {
if (root != null) {
inorderTraversal(root.left);
System.out.print(root.key + " ");
inorderTraversal(root.right);
}
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
// 이진 탐색 트리에 노드를 삽입
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
// 중위 순회로 이진 탐색 트리를 출력
System.out.println("이진 탐색 트리 출력:");
tree.inorderTraversal(tree.root);
// 노드 삭제
tree.delete(20);
tree.delete(30);
tree.delete(50);
// 삭제 후 중위 순회로 이진 탐색 트리를 출력
System.out.println("\n노드 삭제 후 이진 탐색 트리 출력:");
tree.inorderTraversal(tree.root);
}
}
이진 탐색 트리 출력:
20 30 40 50 60 70 80
노드 삭제 후 이진 탐색 트리 출력:
40 60 70 80 위 코드에서 Node 클래스는 이진 탐색 트리의 노드를 정의하며, BinarySearchTree 클래스는 이진 탐색 트리를 구현한다.
Node 클래스의 key 변수는 노드가 가지는 값을 나타내며, left와 right 변수는 왼쪽과 오른쪽 자식 노드를 나타낸다. 생성자는 key 값을 가지고 left와 right 변수를 null로 초기화한다.
BinarySearchTree 클래스의 root 변수는 이진 탐색 트리의 루트 노드를 나타낸다. 생성자는 root 변수를 null로 초기화한다.
insert() 메서드는 이진 탐색 트리에 새로운 노드를 삽입한다. 이진 탐색 트리의 특성을 이용하여 insertNode() 메서드를 이용하여 root 노드에서 삽입할 위치를 찾고, 해당 위치에 노드를 삽입한다.
delete() 메소드는 이진 탐색 트리에서 주어진 key 값을 가진 노드를 삭제한다. 이진 탐색 트리의 특성을 이용하여 deleteNode() 메서드를 이용하여 root 노드에서 삭제할 노드를 찾고, 해당 노드를 삭제한다. 노드를 삭제하는 과정에서는 삭제할 노드의 자식 노드를 적절한 위치로 이동시키는 과정이 포함된다.
minValue() 메서드는 주어진 노드에서 가장 작은 값을 가진 노드를 찾아 반환한다.
inorderTraversal() 메서드는 중위 순회를 수행하여 이진 탐색 트리를 출력한다.
main() 메서드에서는 이진 탐색 트리를 생성하고, 노드를 삽입하고 삭제한 후 중위 순회를 이용하여 이진 탐색 트리를 출력한다.
균형 이진 트리
균형이진트리 개념 다시보기
모든 노드의 좌우 서브트리 높이가 1이상 차이 나지 않는 트리
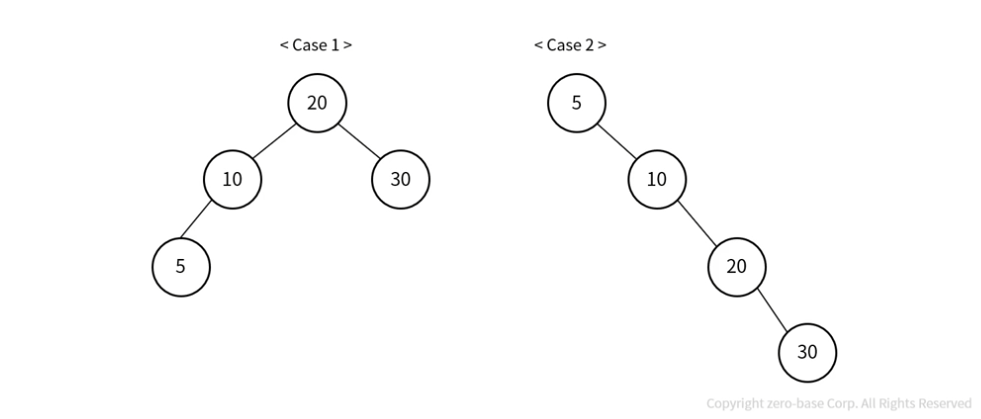
이진 탐색 트리의 편향 발생 (쏠림현상)
Case 1) 이진 탐색트리에 삽입되는 순서 : 20 ▶ 10 ▶ 30 ▶ 5
Case 2) 이진 탐색트리에 삽입되는 순서 : 5 ▶ 10 ▶ 20 ▶ 30
데이터는 같지만 삽입되는 순서에 따라 균형이 깨질 수 있다.
균형 이진 탐색 트리
Balanced Binary Search Tree
- 노드의 삽입과 삭제가 일어날 때 균형을 유지하도록 하는 트리
(AVL트리, Red-Black트리)
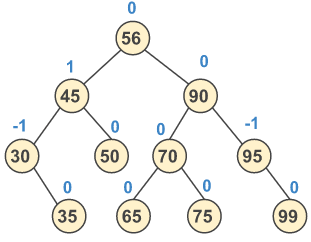
AVL트리
- 노드가 삽입, 삭제될 때 트리의 균형을 확인하고 유지하는 트리
- 각 노드의 BF를 [-1, 0, 1]만 가지게하여 균형을 유지
- BF (Blance Factor)
왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
AVL트리 (리밸런싱)
- 균형이 깨진 경우
a. BF가 '+'이면 왼쪽 서브 트리에 이상이 있음
b. BF가 '-'이면 오른쪽 서브 트리에 이상이 있음 - 회전 연산
a. 단순 회전 - LL, RR
b. 이중 회전 - LR, RL
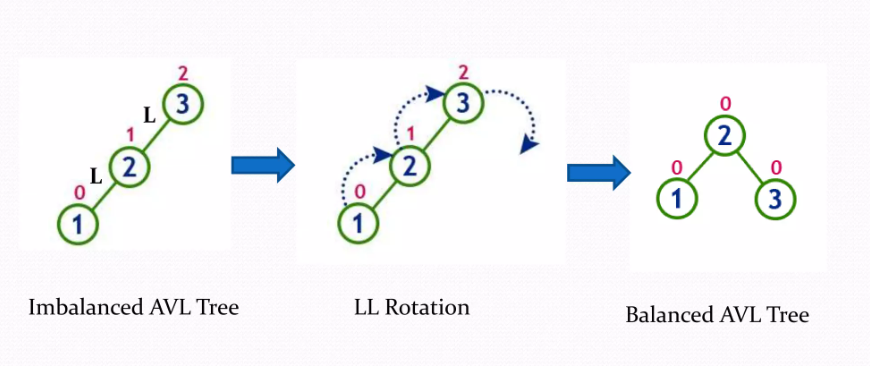
AVL트리 (단순회전)
※ 주의 : LL,RR,LR,RL은 현재상태를 의미, 회전하는 방향을 나타내는 것이 아님.
- LL : Left-Left
회전 1회 / 오른쪽 방향으로 회전
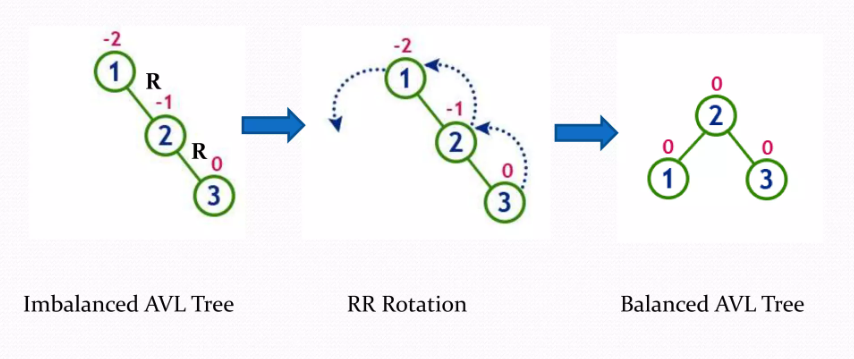
- RR : Right-Right
회전 1회 / 왼쪽 방향으로 회전
AVL트리 (이중회전)
- LR : Left-Right
회전 2회 / 왼쪽 방향으로 회전 후 오른쪽 방향으로 회전
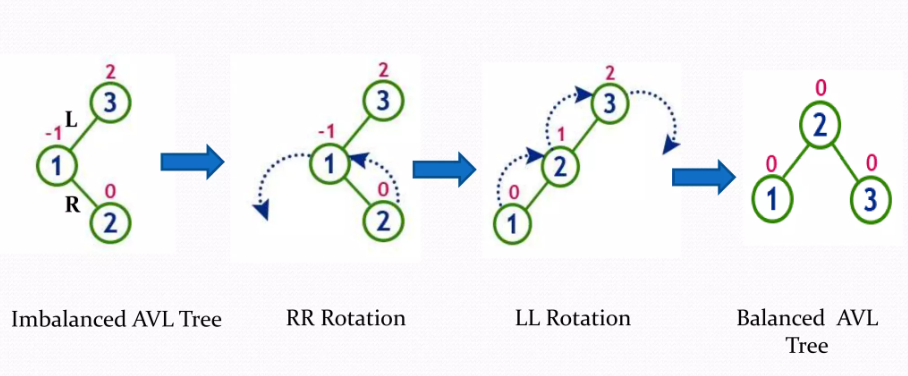
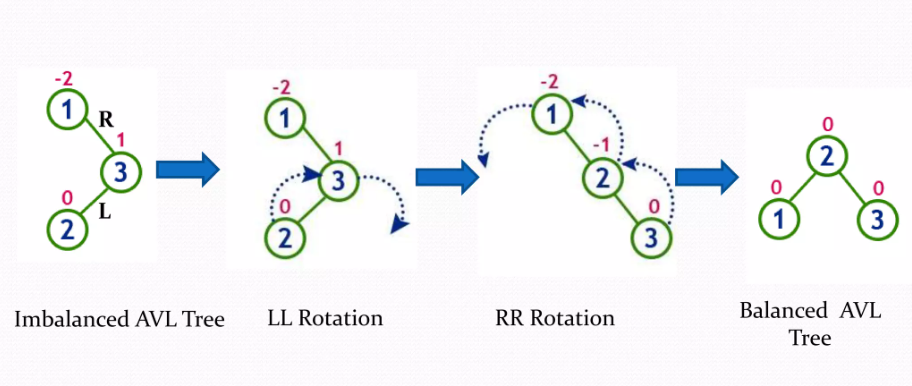
- RL : Right-Left
회전 2회 / 오른쪽 방향으로 회전 후 왼쪽 방향으로 회전
AVL트리 기본 소스 코드
// AVL 트리의 노드 클래스
class Node {
int key; // 노드가 가지는 값
int height; // 노드의 높이
Node left, right; // 왼쪽과 오른쪽 자식 노드
// 생성자
public Node(int item) {
key = item;
height = 1;
left = right = null;
}
}
// AVL 트리 클래스
class AVLTree {
Node root; // AVL 트리의 루트 노드
// 생성자
AVLTree() {
root = null;
}
// 주어진 노드의 높이를 반환하는 메서드
public int height(Node node) {
if (node == null)
return 0;
return node.height;
}
// 두 정수 값 중 큰 값을 반환하는 메서드
public int max(int a, int b) {
return (a > b) ? a : b;
}
// 주어진 노드의 균형 인수를 반환하는 메서드
public int getBalance(Node node) {
if (node == null)
return 0;
return height(node.left) - height(node.right);
}
// 주어진 키 값을 가진 노드를 찾는 메서드
public Node search(Node root, int key) {
if (root == null || root.key == key)
return root;
if (root.key > key)
return search(root.left, key);
return search(root.right, key);
}
// AVL 트리에서 주어진 키 값을 가진 노드를 삽입하는 메서드
public Node insert(Node node, int key) {
// 이진 탐색 트리의 삽입과 같은 방식으로 노드를 삽입
if (node == null)
return (new Node(key));
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
else // 키 값이 이미 존재하는 경우
return node;
// 노드의 높이를 업데이트
node.height = 1 + max(height(node.left), height(node.right));
// 노드의 균형 인수를 계산
int balance = getBalance(node);
// 노드가 불균형 상태인지 확인하고, 적절한 회전을 수행하여 균형을 유지
if (balance > 1 && key < node.left.key)
return rightRotate(node);
if (balance < -1 && key > node.right.key)
return leftRotate(node);
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// AVL 트리에서 주어진 키 값을 가진 노드를 삭제하는 메서드
public Node deleteNode(Node root, int key) {
// 이진 탐색 트리의 삭제와 같은 방식으로 노드를 삭제
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode(root.left, key);
else if (key > root.key)
root.right = deleteNode(root.right, key);
else {
// 삭제할 노드가 단말 노드인 경우
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
// 자식 노드가 없는 경우
if (temp == null) {
temp = root;
root = null;
} else // 한 개의 자식 노드를 가지는 경우
root = temp;
} else {
// 두 개의 자식 노드를 가지는 경우, 오른쪽 서브트리에서 가장 작은 값을 가진 노드를 찾음
Node temp = minValueNode(root.right);
// 찾은 노드의 값을 삭제할 노드에 복사
root.key = temp.key;
// 오른쪽 서브트리에서 찾은 노드를 삭제
root.right = deleteNode(root.right, temp.key);
}
}
// 노드가 하나뿐인 경우
if (root == null)
return root;
// 노드의 높이를 업데이트
root.height = max(height(root.left), height(root.right)) + 1;
// 노드의 균형 인수를 계산
int balance = getBalance(root);
// 노드가 불균형 상태인지 확인하고, 적절한 회전을 수행하여 균형을 유지
if (balance > 1 && getBalance(root.left) >= 0)
return rightRotate(root);
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
if (balance < -1 && getBalance(root.right) <= 0)
return leftRotate(root);
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
// 주어진 노드에서 가장 작은 값을 가진 노드를 반환하는 메서드
public Node minValueNode(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
// AVL 트리에서 오른쪽으로 회전하는 메서드
public Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
// 회전
x.right = y;
y.left = T2;
// 노드의 높이를 업데이트
y.height = max(height(y.left), height(y.right)) + 1;
x.height = max(height(x.left), height(x.right)) + 1;
// 새로운 루트 노드를 반환
return x;
}
// AVL 트리에서 왼쪽으로 회전하는 메서드
public Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
// 회전
y.left = x;
x.right = T2;
// 노드의 높이를 업데이트
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
// 새로운 루트 노드를 반환
return y;
}
// 중위 순회를 수행하는 메서드
public void inorderTraversal(Node node) {
if (node != null) {
inorderTraversal(node.left);
System.out.print(node.key + " ");
inorderTraversal(node.right);
}
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
// AVL 트리에 노드를 삽입
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 30);
tree.root = tree.insert(tree.root, 40);
tree.root = tree.insert(tree.root, 50);
tree.root = tree.insert(tree.root, 25);
// 중위 순회로 AVL 트리를 출력
System.out.println("AVL 트리 출력:");
tree.inorderTraversal(tree.root);
// 노드 삭제
tree.root = tree.deleteNode(tree.root, 25);
// 삭제 후 중위 순회로 AVL 트리를 출력
System.out.println("\n노드 삭제 후 AVL 트리 출력:");
tree.inorderTraversal(tree.root);
}
}AVL 트리 출력:
10 20 25 30 40 50
노드 삭제 후 AVL 트리 출력:
10 20 30 40 50 Red-Black 트리
레드-블랙 트리는 자가 균형 이진 탐색 트리의 일종으로, 균형을 유지하면서도 삽입, 삭제, 검색 등의 연산을 빠르게 처리할 수 있도록 설계된 자료 구조이다. 레드-블랙 트리는 노드마다 레드(Red)나 블랙(Black) 색상을 부여하며, 색상 규칙을 이용하여 트리의 균형을 유지한다.
또한, 레드-블랙 트리는 이진 탐색 트리의 특성을 모두 갖추고 있어 검색 연산의 성능이 우수하다.
레드-블랙 트리의 특성
- 모든 노드는 레드(Red)나 블랙(Black) 중 하나의 색상을 가짐
- 루트 노드는 블랙(Black) 색상을 가짐
- 모든 리프 노드는 블랙(Black) 색상을 가짐
- 노드의 레드(Red) 색상 자식 노드는 모두 블랙(Black) 색상을 가짐
- 모든 경로에는 리프 노드까지 동일한 개수의 블랙(Black) 노드가 존재
레드-블랙 트리에서 노드 삽입, 삭제, 검색 등의 연산을 수행하기 위해서는 색상 규칙을 유지하면서 노드를 추가, 삭제, 탐색하여야 한다. 따라서 레드-블랙 트리는 복잡한 연산이 필요하다. 이에 따라 레드-블랙 트리는 구현하기가 어렵고, 이해하기도 어려운 자료 구조 중 하나이다.
아래는 레드-블랙 트리의 기본 소스 코드이다. (노드 삽입 연산에 대한 구현 포함)
// 레드-블랙 트리의 노드 클래스
class Node {
int key;
boolean color;
Node left, right, parent;
// 생성자
public Node(int key) {
this.key = key;
color = true;
left = right = parent = null;
}
}
// 레드-블랙 트리 클래스
class RedBlackTree {
Node root;
// 생성자
public RedBlackTree() {
root = null;
}
// 노드 삽입 메서드
public void insert(int key) {
Node node = new Node(key);
if (root == null) {
root = node;
root.color = false;
return;
}
Node current = root, parent = null;
while (current != null) {
parent = current;
if (node.key < current.key)
current = current.left;
else if (node.key > current.key)
current = current.right;
else
return;
}
node.parent = parent;
if (node.key < parent.key)
parent.left = node;
else
parent.right = node;
insertFixup(node);
}
// 중위 순회 메서드
public void inorderTraversal(Node node) {
if (node == null)
return;
inorderTraversal(node.left);
System.out.print(node.key + " ");
inorderTraversal(node.right);
}
// 레드-블랙 트리 회전 연산의 보조 메서드
private void rotateLeft(Node node) {
Node rightChild = node.right;
node.right = rightChild.left;
if (rightChild.left != null)
rightChild.left.parent = node;
rightChild.parent = node.parent;
if (node.parent == null)
root = rightChild;
else if (node == node.parent.left)
node.parent.left = rightChild;
else
node.parent.right = rightChild;
rightChild.left = node;
node.parent = rightChild;
}
// 레드-블랙 트리 회전 연산의 보조 메서드
private void rotateRight(Node node) {
Node leftChild = node.left;
node.left = leftChild.right;
if (leftChild.right != null)
leftChild.right.parent = node;
leftChild.parent = node.parent;
if (node.parent == null)
root = leftChild;
else if (node == node.parent.right)
node.parent.right = leftChild;
else
node.parent.left = leftChild;
leftChild.right = node;
node.parent = leftChild;
}
// 레드-블랙 트리 삽입 연산의 보조 메서드
private void insertFixup(Node node) {
while (node.parent != null && node.parent.color) {
if (node.parent == node.parent.parent.left) {
Node uncle = node.parent.parent.right;
if (uncle != null && uncle.color) {
node.parent.color = false;
uncle.color = false;
node.parent.parent.color = true;
node = node.parent.parent;
} else {
if (node == node.parent.right) {
node = node.parent;
rotateLeft(node);
}
node.parent.color = false;
node.parent.parent.color = true;
rotateRight(node.parent.parent);
}
} else {
Node uncle = node.parent.parent.left;
if (uncle != null && uncle.color) {
node.parent.color = false;
uncle.color = false;
node.parent.parent.color = true;
node = node.parent.parent;
} else {
if (node == node.parent.left) {
node = node.parent;
rotateRight(node);
}
node.parent.color = false;
node.parent.parent.color = true;
rotateLeft(node.parent.parent);
}
}
}
root.color = false;
}
}
// 테스트용 메인 클래스
public class RedBlackTreeTest {
public static void main(String[] args) {
RedBlackTree tree = new RedBlackTree();
// 레드-블랙 트리에 노드를 삽입
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
// 중위 순회로 레드-블랙 트리를 출력
System.out.println("레드-블랙 트리 출력:");
tree.inorderTraversal(tree.root);
}
}레드-블랙 트리 출력:
20 30 40 50 60 70 80 위의 전체 코드에서 RedBlackTreeTest 클래스는 테스트를 위한 메인 클래스이다. main() 메서드에서는 레드-블랙 트리 객체를 생성하고, 노드를 삽입한 후 중위 순회로 트리의 내용을 출력한다.
Node 클래스와 RedBlackTree 클래스에서는 노드 삽입, 중위 순회, 회전 등의 기능이 구현되어 있다. insert() 메소드는 노드를 삽입하는 메소드이며, insertFixup() 메소드를 이용하여 삽입 후 색상 규칙을 유지한다. inorderTraversal() 메소드는 중위 순회를 수행하여 트리의 내용을 출력한다. rotateLeft() 메서드와 rotateRight() 메소드는 노드를 회전시키는 메소드이다.
I'm still hungry.