Linear
배열의 0번째 인덱스값부터 차례로 원하는 값을 찾을때까지 배열의 요소를 방문한다
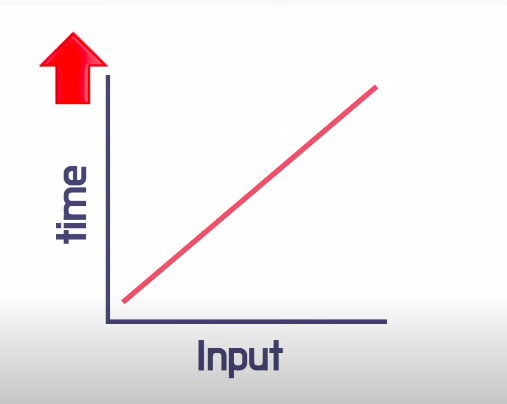
선형검색의 경우 최악의 경우는 우리가 찾는 요소가 마지막 인덱스값이거나 배열에 존재하지 않는 경우이다. 즉, 배열의 크기가 커질수록 원하는 요소를 찾는데 거치는 단계 또한 많아질 것이다. 이를 Linear Time Complexity(선형 시간복잡도)라고 한다.
예를 들어, 10000개의 데이터를 갖는 배열에서 요소를 찾을때, 최악의 경우 10000개의 요소를 모두 확인해야 한다.
Binary Search
오직 정렬된 배열에서만 사용할 수 있다
어떤 알고리즘은 특정 자료구조에서만 사용할 수 있는데, Binary Search 알고리즘은 오직 정렬된 배열(sorted array)에서만 사용가능하다.
정렬된 배열에 요소를 추가하려면 정렬된 배열의 요소와 각각 크기를 비교해 어디에 위치해야할지를 결정해야하므로 선형 알고리즘보다 오래걸리지만 정렬된 배열에서 검색하는 것은 굉장히 빠르다.
앞서 보았던 선형 탐색은 배열의 크기가 커질수록 거치는 단계가 많아졌지만, 이진탐색은 배열의 크기가 2배가 되어도 오직 1단계만 늘어난다. 따라서 크기가 큰 배열일수록 이진탐색이 효율적이다.
앞서 생각해본 예시처럼 10000개의 데이터를 가진 배열에서 요소를 찾을때, 이진탐색은 최악의 경우에도 14번만 탐색하면 된다.
1회 10000/2 = 5000
2회 5000/2 = 2500
3회 2500/2 = 1250
4회 1250/2 = 625
5회 625/2 = parseInt(312.5) = 312
6회 312/2 = 156
7회 156/2 = 78
8회 78/2 = 39
9회 39/2 = parseInt(19.5) = 19
10회 19/2 = parseInt(9.5) = 9
11회 9/2 = parseInt(4.5) = 4
12회 4/2 = 2
13회 2/2 = 1
14회 발견