시간복잡도

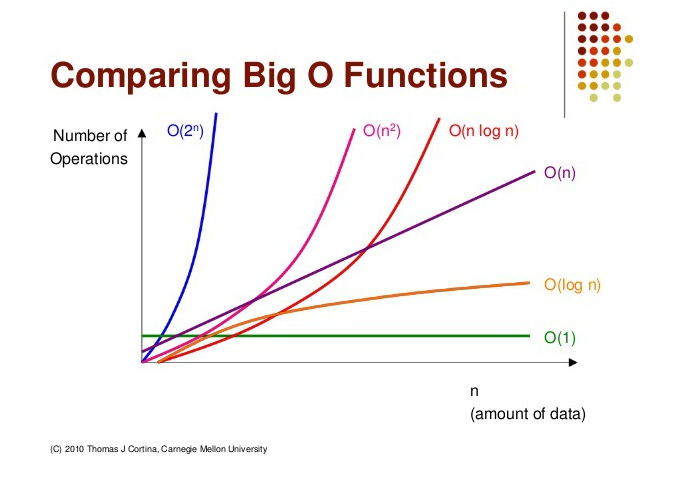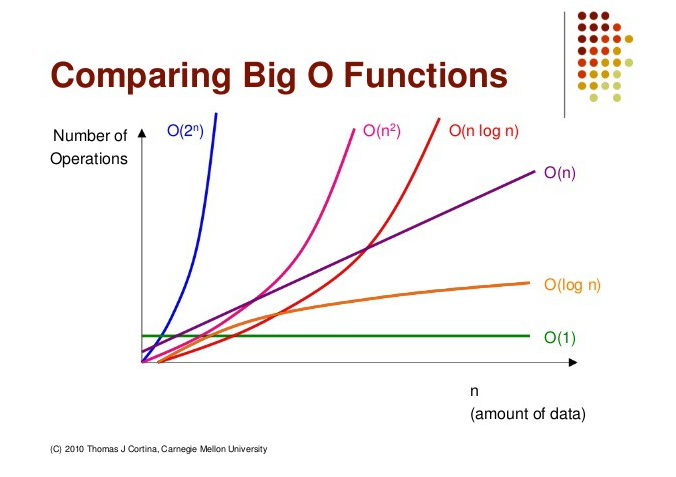
시간 복잡도의 유형

Big-O(빅-오)
Big-Ω(빅-오메가)
Big-θ(빅-세타)

알고리즘의 빠르기를 어떻게 표현할까?

알고리즘의 빠르기는 '시간'으로 표현하지 않는다. 하드웨어마다 걸리는 '시간'은 상이할 수 있기 때문이다. 예를 들어, 같은 알고리즘이라도 누군가의 컴퓨터에서는 시간이 적게 걸리고, 다른 누군가의 컴퓨터에서는 시간이 오래 걸릴 수 있다.

따라서, 알고리즘의 빠르기는 '거치는 단계'로 표현한다. 선형탐색은 배열의 요소를 하나씩 탐색했었다. 즉, 입력 배열의 길이가 N이라면, N단계를 거쳐야 한다. 즉, 선형탐색의 시간복잡도는 O(N)이라고 표현할 수 있다.

Big O notation

O(1)

배열의 크기가 기하급수적으로 커지더라도 그에 따라 거치는 단계가 커지지 않는 것이 핵심이다. 따라서 아래 함수에서 console.log(arr[0))을 2번 하든, 3번하든, 100번을 하든 배열의 크기에 따라 달라지지 않으므로 O(1)로 표현한다. 즉, Big O 표기법에서 괄호 안의 상수값이 1인지 2인지 3인지, 100인지는 전.혀. 중요하지 않다.

//배열의 첫번째 요소를 콘솔에 찍는 함수
function big_O_1(arr){
  console.log(arr[0])
}
//이 함수는 입력된 배열의 크기에 관계없이 한번의 단계만 거친다 
//이 함수의 시간복잡도는 constant time이라고 할 수 있다. 입력된 배열의 크기에 관계없이 늘 동일한 횟수의 단계를 거친다.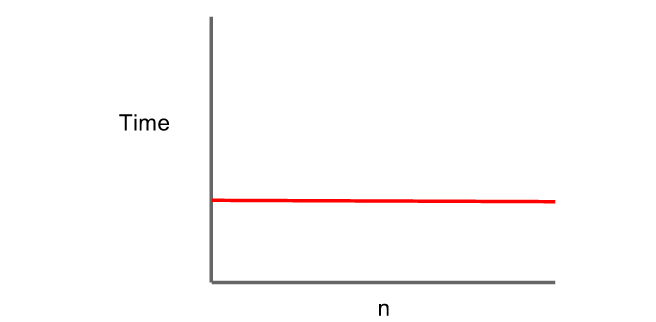

O(n) ===> 선형탐색 시간복잡도

//배열의 모든 요소를 콘솔에 찍는 함수
function big_O_n(arr){
  for(const el of arr){
    console.log(el)
  }
}
//이 함수는 입력된 배열의 크기에 따라 실행되는 단계 횟수가 늘어난다.
//이 함수의 시간복잡도는 n이라고 할 수 있다. 입력된 배열의 크기만큼의 단계를 거친다.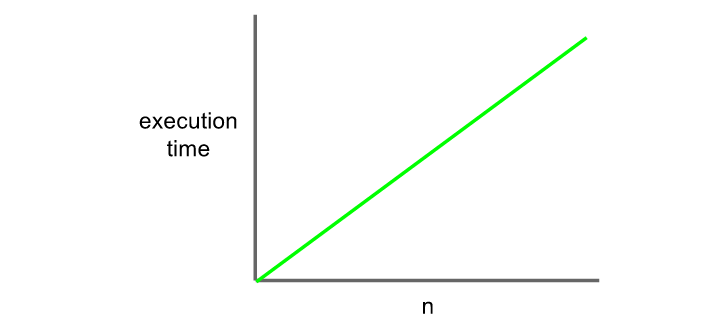

O(n^2)

//반복문으로 방문한 배열의 요소에 대해 중첩 반복문으로 처음부터 마지막 요소까지 콘솔에 찍는 함수
function big_O_n^2(arr){
  for(let i=0;i<arr.length;i++){
    for(let j=0;j<arr.length;j++){
      console.log(arr[i],arr[j]);
    }
  }
}
//이 함수는 입력된 배열의 크기에 제곱만큼 실행 횟수를 갖는다.
//이 함수의 시간 복잡도는 n^2이라고 할 수 있다.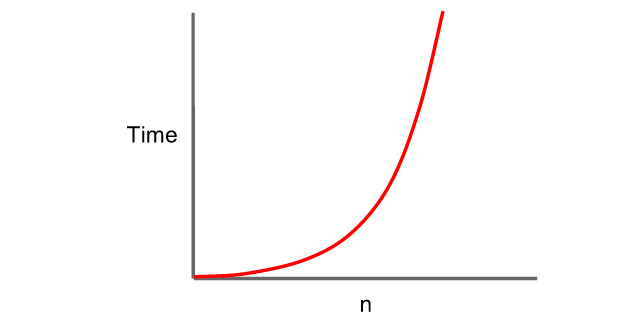 

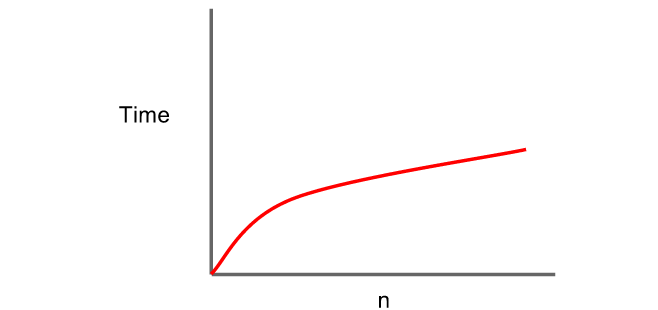
O(log n) ===> 이진탐색 시간복잡도

//arr이 정렬되어있을때, 이진탐색으로 요소의 인덱스 찾기
function big_O_logn(arr, k){
  let left = 0;
  let right = arr.length-1; 
  
  while(left<=right){
    let middle = parseInt((left+right)/2);
    if(arr[middle] === k){return middle}
    else if(arr[middle] < k){
      left = middle+1;
    }
    else{
      right = middle-1;
    }
  }
  return -1;
}

O(2^n)

function fibonacci(n){ //첫번째 항이 1인 피보나치 수열
  if(n<=1){return 1}
  return fibonacci(n-1) + fibonacci(n-2);
}