[자료구조] 그래프

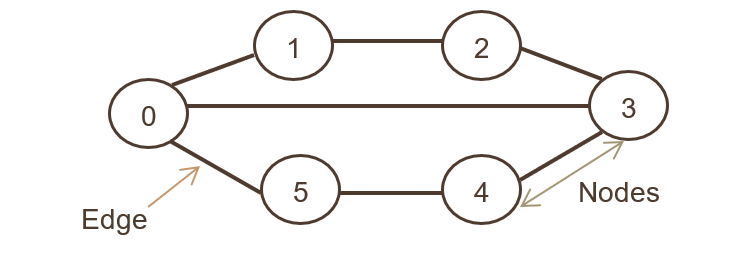
그래프

• 그래프는 비선형적 데이터 구조로 vertice(또는 node)와 그 vertice를 연결하는 edge로 구성되어있다.
• 방향성과 가중치를 가질 수 있고, self-loop, loop처럼 순환할 수 있다.
• 그래프는 네트워크 모델을 가지며, 실생활에서 많이 사용되는 자료구조로 도시간의 경로, 페이스북과 같은 소셜네트워크에서도 사용된다.
  • 예를들어, 페이스북에서 각 유저는 vertex이며 각 유저는 edge로 연결된다.
• 그래프의 순회는 DBS 또는 BFS로 이루어진다.
• 트리와 다르게 루트노드, 부모-자식 개념이 없다. (트리는 사이클을 가지지 않는 연결 그래프라고 할 수 있다)

그래프 관련 용어

• 정점(vertex): 노드라고도 하며, 정점에는 데이터가 저장된다.
• 간선(edge): 정점을 연결하는 선
• 인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점
• 단순경로(simple path): 경로 중에서 반복되는 정점이 없는 한붓그리기 같은 경우
• 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
• 진출차수(out-degree): 방향 그래프에서 한 노드에서 외부로 향하는 간선 수
• 진입차수(in-degree): 방향 그래프에서 한 노드로 들어오는 간선 수
• 경로길이(path length): 경로를 구성하는데 사용된 간선 수
• 사이클(cycle): 시작정점과 종료정점이 동일한 단순경로
• 자기루프(self loop): 정점에서 진출한 간선이 곧바로 자기 자신에게 진입하는 경우로 다른 정점을 거치지 않는 것이 특징이다.

그래프 종류

무방향 그래프(undirected graph)

• 두 정점을 연결하는 간선에 방향이 없는 그래프

방향 그래프(directed graph)

• 두 정점을 연결하는 간선에 방향이 있는 그래프

가중치 그래프(weighted graph)

• 간선에 가중치가 할당된 그래프로 두 정점을 이동할 때 비용이 드는 그래프

연결 그래프(connected graph)

• 모든 정점들이 빠짐없이 간선에 의해 연결된 그래프

비연결 그래프(disconnected grahp)

• 하나라도 연결되지 않은 정점 있는 그래프

신장트리(spanning tree)

• 그래프의 모든 정점을 포함하는 트리로 하나의 그래프에서 여러개의 신장트리가 나올 수 있다.
• 간선의 개수는 (정점-1)개이다.
• 사이클을 포함해서는 안된다.
  

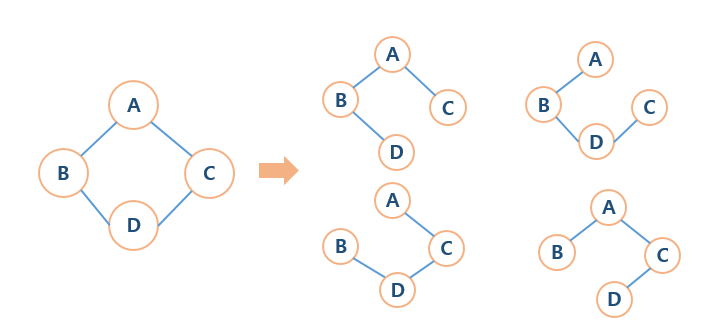
최소신장트리(Minimal Spanning Tree/MST)

• 간선에 가중치가 부여되어있을때, 가중치를 고려해 최소비용의 신장트리를 구할 수 있다.
• 크루스칼, 프림 알고리즘을 이용해서 구할 수 있다.

그래프 구현

인접이란, 두 정점을 연결하는 간선이 있는 것을 말한다.

• 인접행렬
  2차원 배열의 형태로 나타낼 수 있으며, 비가중치 그래프의 경우, 0과 1로 연결을 나타낼 수 있고, 가중치 그래프의 경우, 거리, 비용 등의 값으로 연결을 나타낼 수 있다. 정점 A가 정점 B와 인접하는지 확인할 때 유용하다.
  • (시간) 두 정점이 연결되었는지 확인하는데 걸리는 시간은 O(1)
  • (시간) 한 정점에 연결된 모든 정점을 확인하는데 걸리는 시간 O(V) (여기서 V는 정점의 개수)
  • (시간) 그래프에 존재하는 모든 간선의 개수는 인접행렬을 모두 조사해야하므로 O(V^2)이 걸린다.
  • (공간) V개의 정점을 가진 인접행렬은 간선의 수와 무관하게 O(V^2)만큼의 공간복잡도를 갖는다.

👉 간선의 수가 많고, 정점간 연결여부를 빠르게 파악해야할 때 적합

//directed, unweighted graph
//여기서 배열의 인덱스를 정점으로 사용한다. 
class GraphiWithAdjacencyMatrix {
  constructor() {
    this.matrix = [];
  }
  
  addVertex() {
    const currentLength = this.matrix.length;
    for(let i=0; i<currentLength; i++) {
      this.matrix[i].push(0);
    }
    this.matrix.push(new Array(currentLength+1).fill(0));
  }
  
  contains(vertex) {
    if(vertex<this.matrix.length) {
      return true;
    }
    return false;
  }
  
  addEdge(from, to) {
    const currentLength = this.matrix.length; //정점의 개수 (최소 정점 값은 0)
    if(from === undefined || to === undefined) return;
    if(from > currentLength-1 || to > currentLength-1 || from < 0 || to < 0) return;
    this.matrix[from][to] = 1;
  }
  
  hasEdge(from, to) {
    return !!this.matrix[from][to];
    //matrix[from][to]는 0, 1, undefined가 나올 수 있는데, true, false로만 리턴하기 위해서는 !!를 작성해주면 된다.
  }
  
  removeEdge(from, to) {
    const currentLength = this.matrix.length;
    if(from === undefined || to === undefined) return;
    if(from > currentLength-1 || to > currentLength-1 || from < 0 || to < 0) return;
    this.matrix[from][to] = 0;
  }

---

• 인접리스트
  각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 저장한다. 모든 경우의 수를 저장해 메모리를 많이 차지하는 인접행렬과 다르게, 메모리를 효율적으로 사용해야하는 경우 유용하다.
  • (시간) 두 정점이 연결되었는지 확인하는데 걸리는 시간은 리스트를 선형탐색해야하므로 최악의 경우 O(V)이다.
  • (시간) 한 정점에 연결된 모든 정점을 확인하기 위해서는 간선의 개수만큼 확인하면 되므로 O(E)이다. 이때 드물지만 최악의 경우, 한 노드가 다른 모든 노드와 연결되어있을 경우, E=V^2이므로 O(V^2)이다.
  • (시간) 그래프 내에 존재하는 모든 간선의 수는 O(V+E)이다.
  • (공간) 정점마다 인접리스트를 확인해야하므로 O(V+E)의 공간복잡도를 갖는다.

👉 간선의 수가 적고, 메모리를 효율적으로 사용해야하는 경우 적합

class GraphWithAdjacencyList {
  //undirected graph
  constructor() {
    this.vertices = {};
  }
  
  addVertex(vertex) {
    this.vertices[vertex] = this.vertices[vertex] || [];
  }
  
  contains(vertex) {
    return !!this.vertices[vertex];
  }
  
  addEdge(fromVertex, toVertex) {
    if(!this.contains(fromVertex) || !this.contains(toVertex)) return;
    
    if(!this.hasEdge(fromVertex, toVertex)) {
      this.vertices[fromVertex].push(toVertex);
    }
    
    if(!this.hasEdge(toVertex, fromVertex)) {
      this.vertices[toVertex].push(fromVertex);
    }
  }
  
  hasEdge(fromVertex, toVertex) {
    if(!this.contains(fromVertex)) {
      return false
    }
    return this.vertices[fromVertex].includes(toVertex);
  }
  
  removeEdge(fromVertex, toVertex) {
    if(!this.contains(fromVertex) || !this.contains(toVertex)) return;
    
    if(this.hasEdge(fromVertex, toVertex)) {
      const toVertexIndex = this.vertices[fromVertex].indexOf(toVertex);
      this.vertices[fromVertex].splice(toVertexIndex,1);
      //무방향 그래프이므로, 정점 A의 리스트에 B가 있다면, 정점 B의 리스트에도 A가 있으므로 indexOf의 값이 -1이 나올 수 없다.
    }
    
    if(this.hasEdge(toVertex, fromVertex)) {
      const fromVertexIndex = this.vertices[toVertex].indexOf(fromVertex);
      this.vertices[toVertex].splice(fromVertexIndex,1);
    }
    return;
  }
      
  removeVertex(vertex) {
    if(this.contains(vertex)) {
      while(this.vertices[vertex].length > 0) {
        this.removeEdge(this.vertices[vertex][0], vertex);
      }
      delete this.vertices[vertex];
    } 
  }

그래프 순회

DFS 깊이우선탐색

노드의 자식노드들을 우선으로 더이상 자식 노드가 없을때까지 탐색한다. stack 또는 재귀를 활용해 구현한다. 시간복잡도는 O(V+E)를 갖는다.

BFS 넓이우선탐색

노드의 같은 레벨의 노드들(형제노드)을 우선으로 같은 레벨의 노드가 없을때까지 탐색한다. 큐를 활용해 구현한다. 시간복잡도는 O(V+E)를 갖는다.

reference

• 자료구조 그래프
• Algorithms: Graph Search, DFS and BFS