Binary Search Tree를 설명해보세요
Keyword
key, 탐색, 편향 트리, worst case
Script
Binary Search Tree는 효율적인 탐색을 위해 고안된 binary tree의 일종입니다. Binary Search Tree는 binary tree에 몇 가지 규칙을 추가하여 특정 데이터를 쉽게 찾을 수 있게 만듭니다. 먼저, 각 Node에 저장된 key는 유일하고, 부모 Node의 key를 기준으로 왼쪽 자식 Node는 더 작은 key 값을 가지고 오른쪽 자식 Node는 더 큰 key 값을 가집니다. 그리고 재귀적으로 Sub Tree 또한 Binary Search Tree입니다.
Binary Search Tree는 평균적으로 삽입, 삭제, 탐색에 O(log n)의 시간복잡도를 가집니다. log n은 Tree의 height입니다. 하지만 최악의 경우 O(n)의 시간복잡도를 가지는데, 이는 한 쪽으로만 자식 Node가 추가되는 경우에 Binary Search Tree가 편향 트리가 되기 때문입니다.
추가로, 이를 해결하는 Rebalancing 기법이 있고, Red-black Tree가 대표적인 예시입니다.
Additional
Binary Search Tree와 Hash Table
Hash table을 사용하면, 삽입과 탐색 그리고 삭제 연산을 평균 O(1) 시간복잡도로 사행할 수 있는데 굳이 Binary Search Tree를 사용하는 경우는 언제일까?
1. inOrder 순회를 통해 Tree 속 데이터를 정렬하여 갖고 올때
Hash Table은 데이터 간의 순서 관계를 저장할 수 없는 자료구조이기 때문에, 일반적인 정렬 알고리즘이 필요한 반면, Binary Search에서는 inOrder 순회만으로 빠르게 정렬이 가능하다.
2. 메모리가 제한되어있을 때
Binary Search Tree는 필요한 원소만큼의 공간을 할당하는 반면, Hash Table은 적중률을 높이기 위해 원소의 개수 이상의 메모리를 항상 유지하며 적재율을 관리해야 한다.
배열로 Binary Search Tree 구현하기
Binary Search Tree를 간단하게 1차원 배열로 구현해볼 수 있다.
Root Node의 index는 1로 설정하고서, 어떤 값이 들어왔을 때, 현재 Node를 기준으로 더 큰 값이라면 2 index + 1로 이동하여 재귀적으로 다시 삽입을 시도한다. 반대로 더 작은 값이라면 2 index로 이동하여 삽입을 시도한다.
이외에도 Node, Tree를 하나의 class로 만들어서 구현할 수도 있다.
주어진 Tree가 Binary Search Tree인지 확인하기
일단 첫번째 방법으로, Binary Search Tree를 중위 순회(inorder traversal)를 사용하여 탐색한다. 이 때 만약 오름차순으로 정렬되어 있지 않다면, Binary Search Tree가 아니라는 것을 알 수 있다.
두번째 방법은, Binary Search Tree의 특징을 통해 재귀적으로 탐색하는 것이다.
1. 왼쪽 자식 Node가 Root Node보다 작고, 오른쪽 자식 Node가 Root Node보다 큰지
2. 왼쪽 Sub Tree의 최댓값이 루트보다 작고, 오른쪽 Sub Tree의 최솟값이 Root Node보다 작은지
이 두가지 사항을 확인하는 재귀적 알고리즘을 통해 Binary Search Tree 여부를 확인할 수 있다.
이때 2번 과정이 중요하다. 재귀 함수를 만들때, 지금까지의 최소값 경계과 최댓값 경계을 인자로 넘겨주도록 함수를 설계한다.
그리고 왼쪽 Node를 탐색할 때는 더 작은 값이 되기 때문에, 현재까지의 최댓값 경계와 현재 Node의 값 중 작은 것을 다음 Node의 최댓값 경계로 넘겨준다. 반대로 오른쪽 Node를 탐색할 때는 더 큰 값이 되어야 하기 때문에, 현재까지의 최솟값 경계와 현재 Node의 값 중 큰 것을 다음 Node의 최솟값 경계로 넘겨준다.
이후 base condition으로 다음 Node의 값이 이 경계와 맞닿아있거나 벗어나는 경우에 BST는 not valid 하도록 함수를 설계할 수 있다.
이 방법을 사용하면, 모든 Node를 탐색하기 때문에, Node의 개수가 n일때, O(n)의 시간 복잡도를 가지게 된다.
private boolean checkValidBST(TreeNode root, long low, long high) {
if (root.val <= low || root.val >= high) {
return false;
}
boolean result = true;
if (root.left != null) {
result &= checkValidBST(root.left, low, Math.min(high, root.val));
}
if (root.right != null) {
result &= checkValidBST(root.right, Math.max(low, root.val), high);
}
return result;
}
public boolean isValidBST(TreeNode root) {
if(root == null) {
return true;
}
return checkValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}Binary Search Tree에서 Node 삭제
case 1: 자식 Node가 없는 Node는 바로 Tree에서 Node를 제거
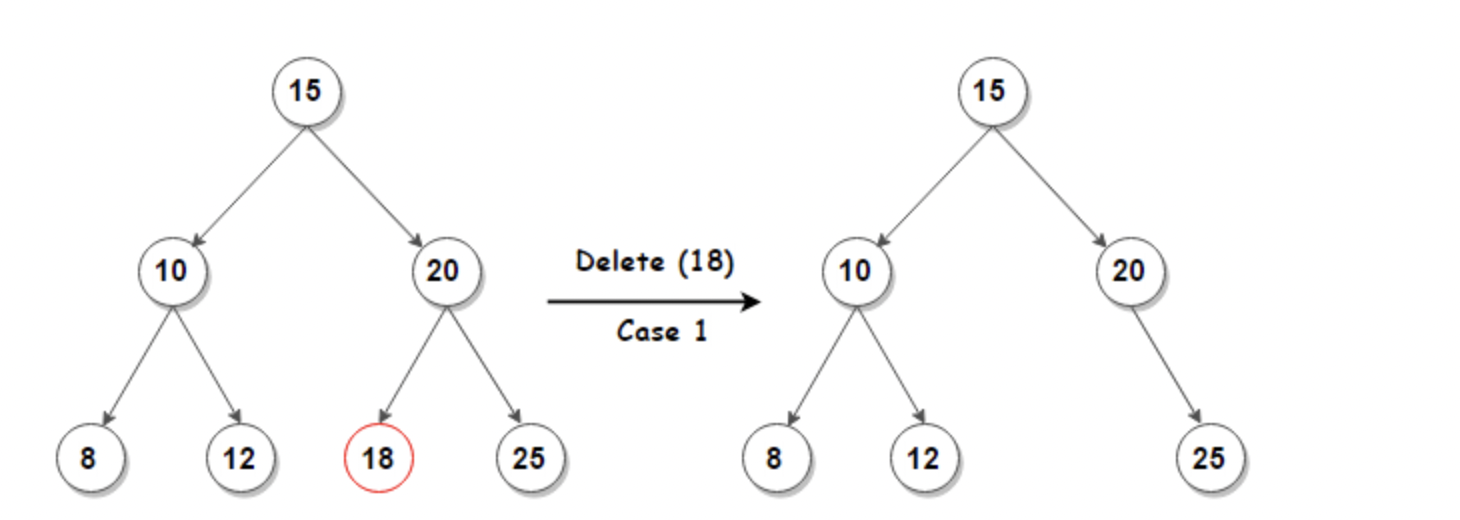
case 2: 자식 Node가 1개 있는 경우는 해당 Node 제거 후 자식 Node로 교체
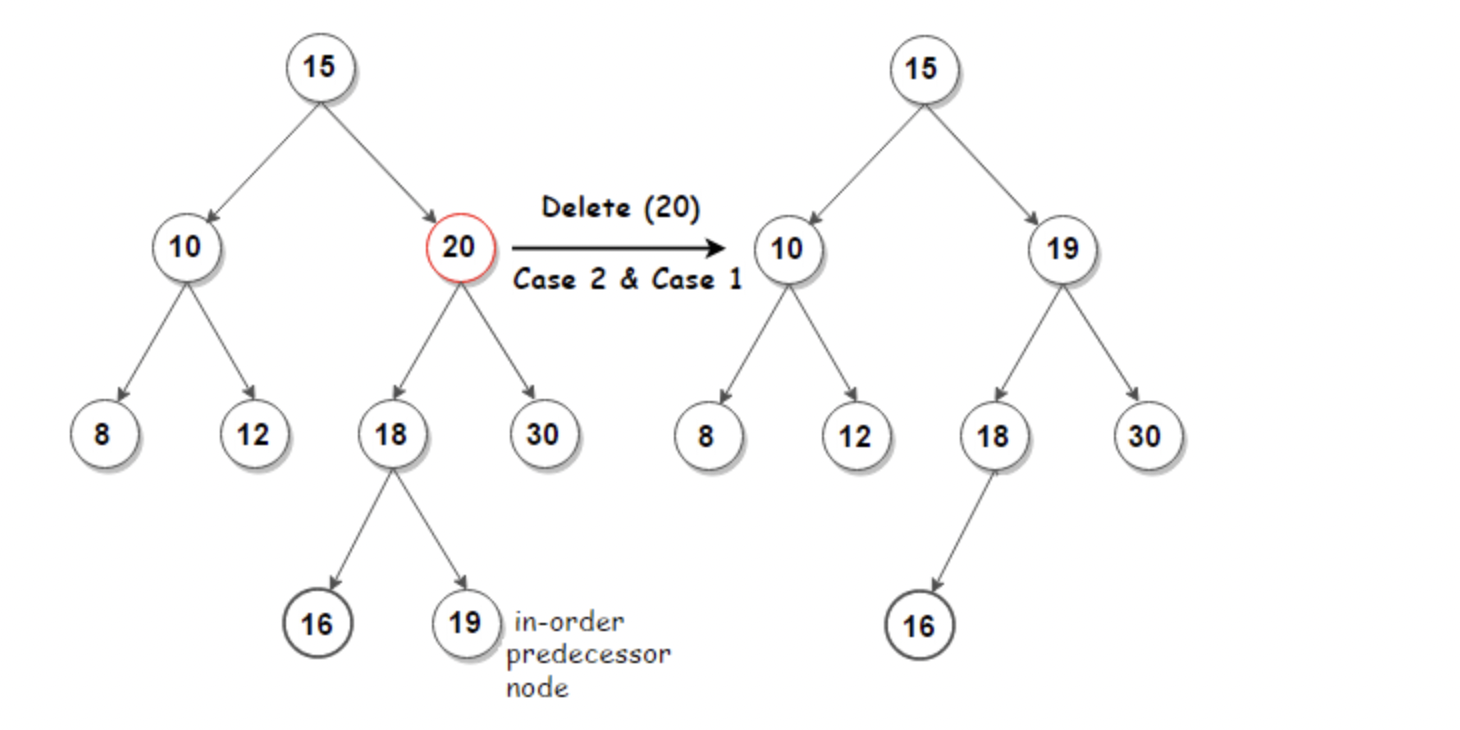
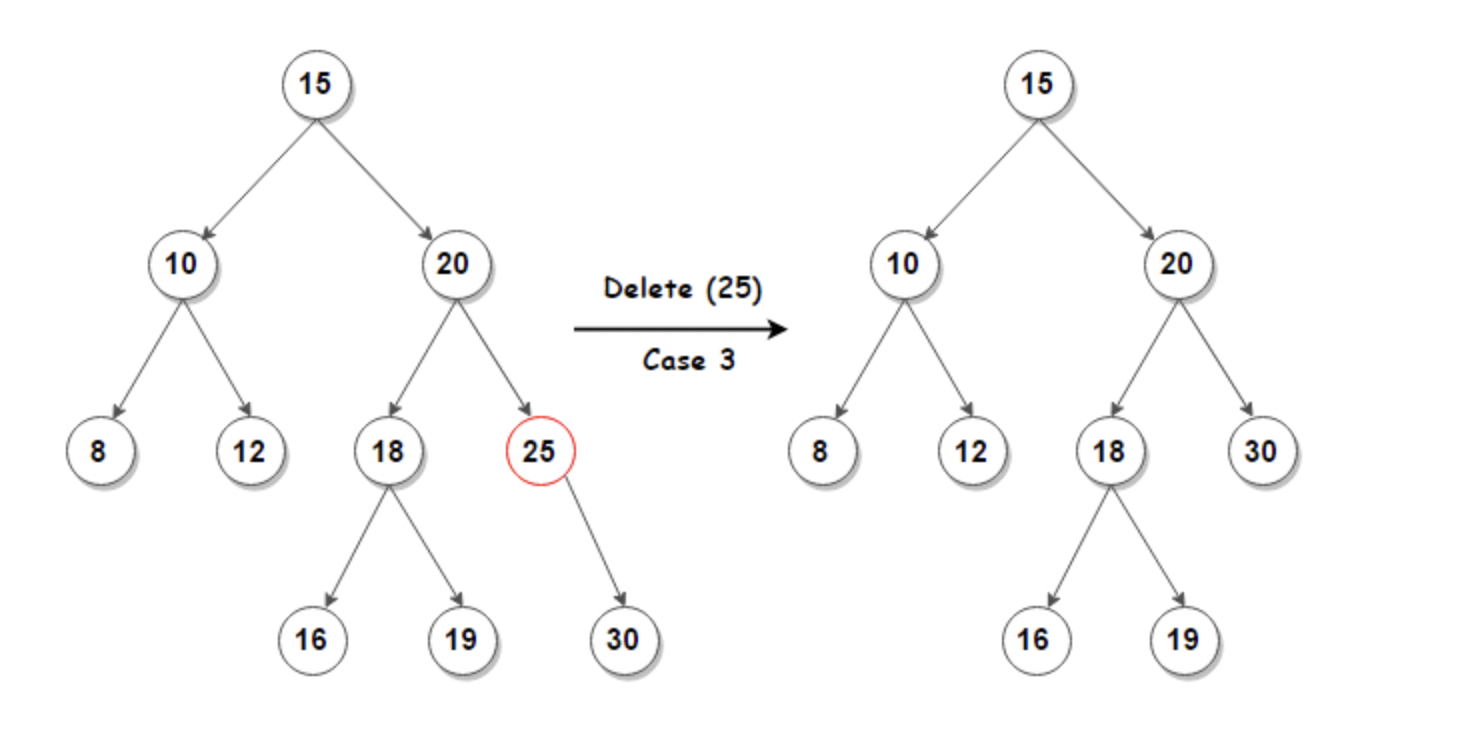
case 3: 자식 Noderk 2개 있는 경우는 해당 Node 제거 후 inOrder 순회 기준 이전 Node로 교체