Binary Tree에 대해 설명해보세요
Keyword
2개의 Sub Tree, 재귀적, level, height
Script
Binary Tree는 Root Node를 기준으로 2개의 Sub Tree로 나뉘어집니다. 그리고 재귀적으로 그 나누어진 Tree도 모두 Binary Tree이어야 합니다. 즉, 모든 노드가 최대 2개의 자식을 가지는 Tree 자료구조입니다. Root Node를 기준으로 level은 0부터 시작하고, 해당 Tree의 최고 level을 height라고 합니다.
Additional
Perfect Binary Tree, Complete Binary Tree, Full Binary Tree
Perfect Binary Tree(포화 이진 트리)는 Tree의 모든 Level이 Node로 가득 차있는 Binary Tree이다. 이때, Tree의 Node 개수는 2^k-1 개가 된다.
Complete Binary Tree(완전 이진 트리)는 Root Node로 부터, 각 Level을 전부 채우면서 왼쪽 Node부터 순차적으로 채워나간 Binary Tree를 의미한다.
Full Binary Tree(전 이진 트리)는 모든 Node가 0개 또는 2개의 자식 Node를 갖는 Tree이다.
배열로 Binary Tree를 구현
배열로 Binary Tree를 구현할 때, index를 통해 부모-자식 관계를 정의할 수 있다.
Root Node를 index 1에서 시작한다고 하면 다음과 같은 관계를 정의할 수 있다.
parent(i) = i/2
left_child(i) = 2i,
right_child(i) = 2i + 1전위 순회, 중위 순회, 후위 순회
전위 순회(PreOrder)는 Root Node를 시작으로 왼쪽 자식, 오른쪽 자식 순으로 순회한다.

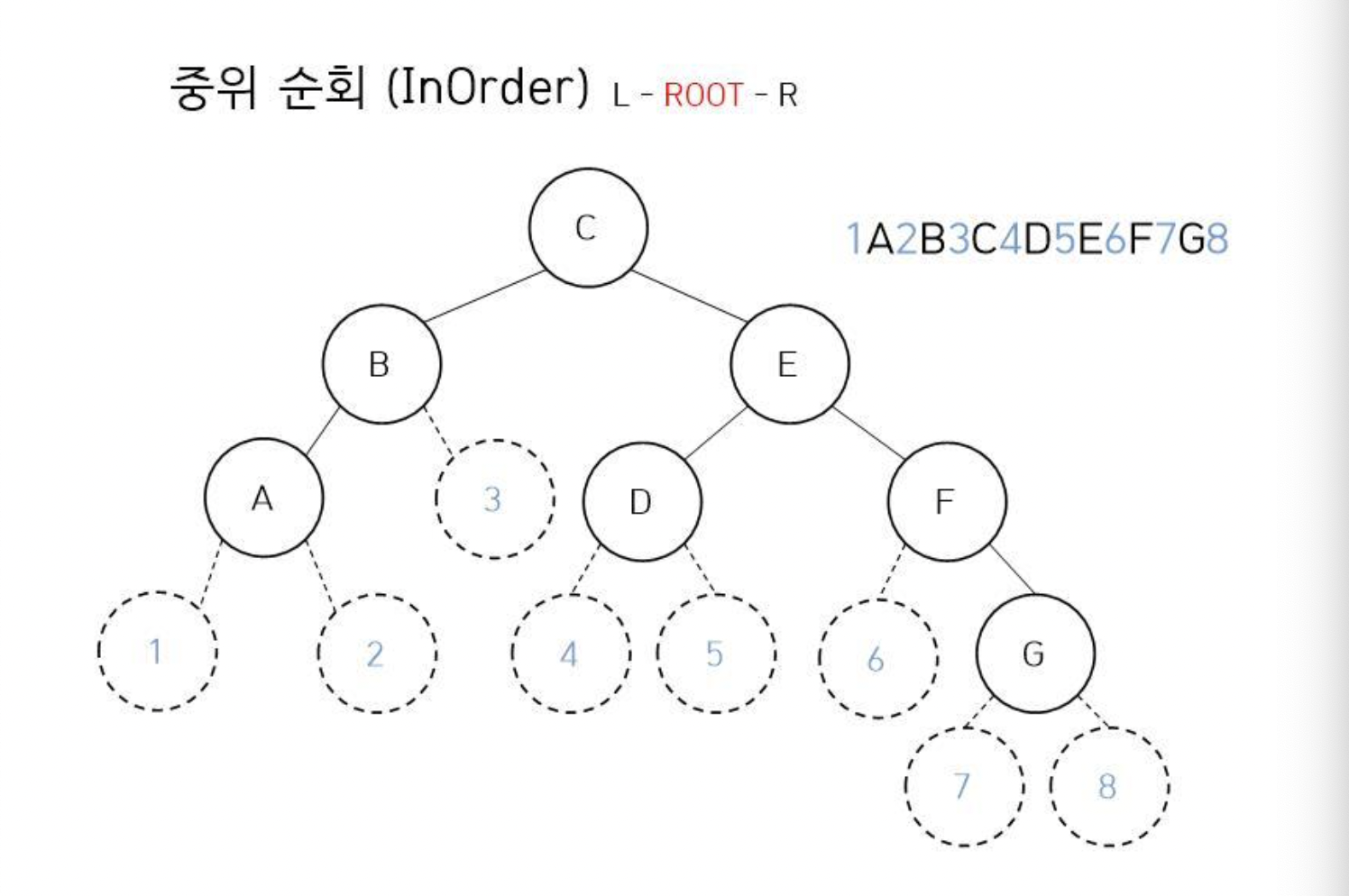
중위 순회(InOrder)는 왼쪽 자식을 시작으로 Root Node, 오른쪽 자식 순으로 순회한다.
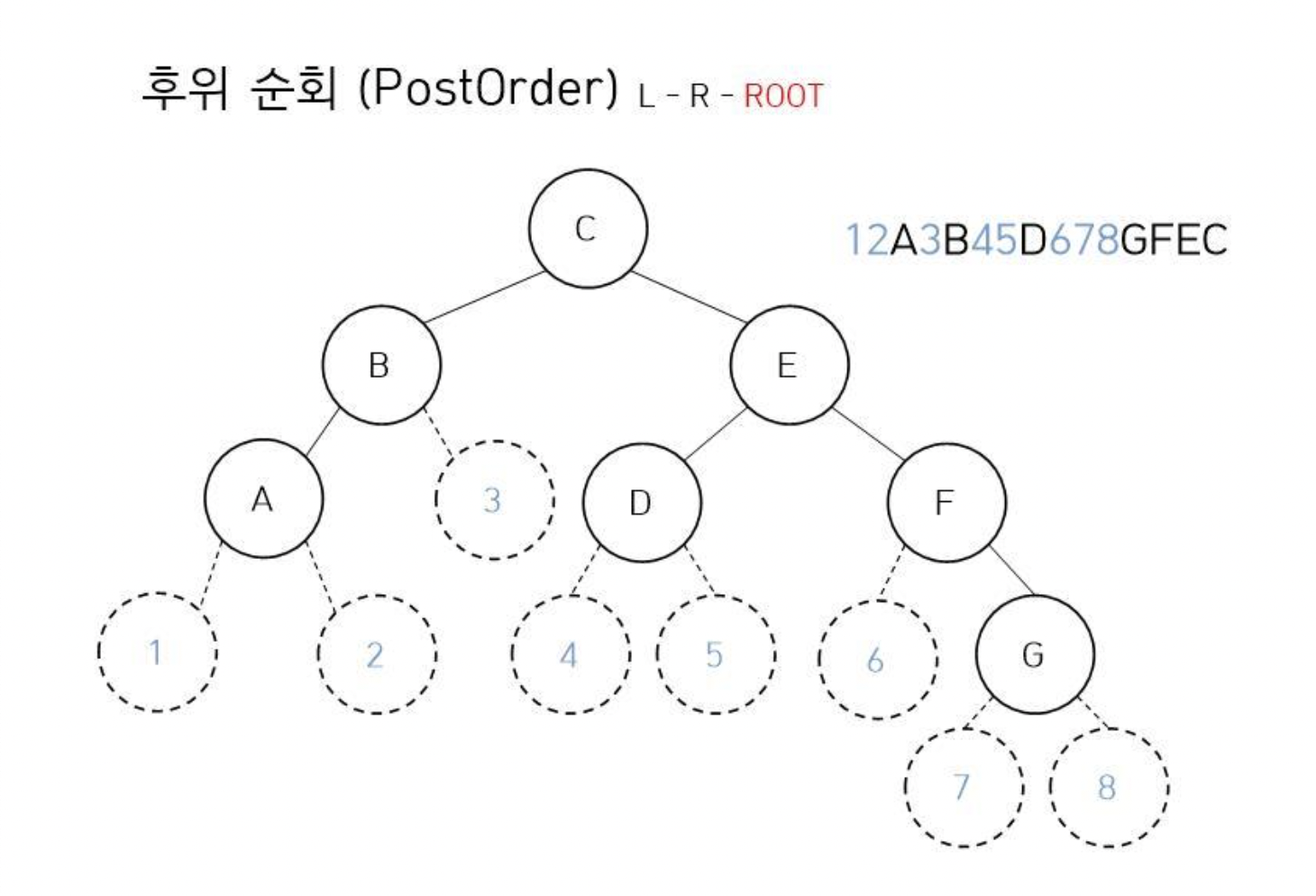
후위 순회(PostOrder)는 왼쪽 자식을 시작으로 오른쪽 자식, Root Node 순으로 순회한다.
주어진 Node와 같은 level에서의 다음 Node를 찾는 알고리즘
BFS로 Tree를 탐색하게 되면, 같은 level에 있는 모든 Node를 탐색한 후 다음 level로 넘어가기 때문에, 쉽게 같은 level에서의 다음 Node를 찾을 수 있다.
Binary Tree에서 주어진 노드의 모든 조상 찾기
[ pending... ]
