벨만포드 알고리즘
한 정점으로부터 다른 모든 정점까지의 최단 경로를 탐색할 때 사용하는 알고리즘
특징
-
한 지점에서 다른 모든 정점들까지의 최단 경로를 구할 수 있다.
-
매 순회 마다 모든 간선을 전부 확인한다.
-
음수 간선을 해결할 수 있다.
-
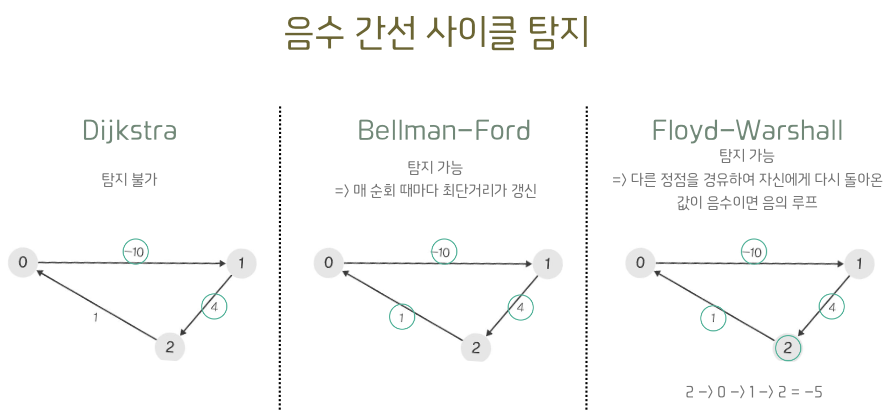
음수 간선 순환을 확인할 수 있다.
장단점
장점
- 음수 간선이 포함된 상황에서도 사용 가능
- 음수 간선 순환 확인 가능
단점
- 다익스트라에 비해 높은 시간복잡도
- 단일 출발지 최단 경로
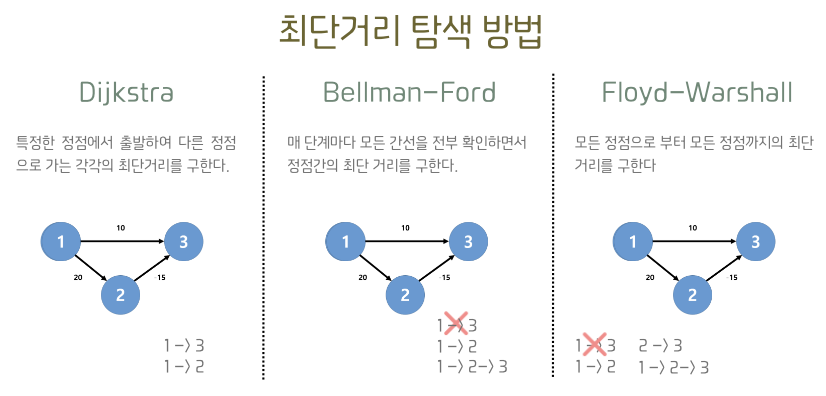
비교
최단거리 탐색 방법
음수 간선 사이클 탐지
시간 복잡도
| Dijkstra | Bellman-Ford | Floyd-Warshall |
|---|---|---|
| O(E log V) | O(V * E) | O() |
활용 사례
-
실시간 교통 정보
교통 혼잡을 줄이는 경로를 찾는데 사용할 수 있음
(교통량의 증가를 음의 가중치로 나타내고 이를 처리할 수 있기 때문) -
최적 전력 분배
전력망에서 전력 손실을 최소화 하는 경로를 찾는데 사용
Relaxation
간선 정보를 토대로, 전체 간선을 검사하여 최단 거리 결과 테이블을 갱신하는 행위
- 벨만 포드는 (n-1)번 이 과정을 반복하면 최단 경로가 결정된다.
- 만약, n번째에도 결과 테이블이 갱신된다면 음의 간선 사이클이 발생했음을 알 수 있다.
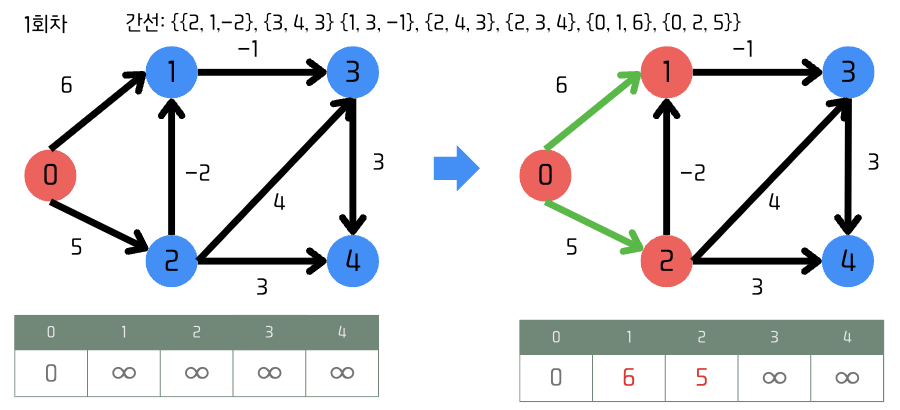
Relaxation의 예시 및 과정
주어진 간선 정보를 순서대로 검증했을 때의 각각 회차별 결과 테이블
-
1회차
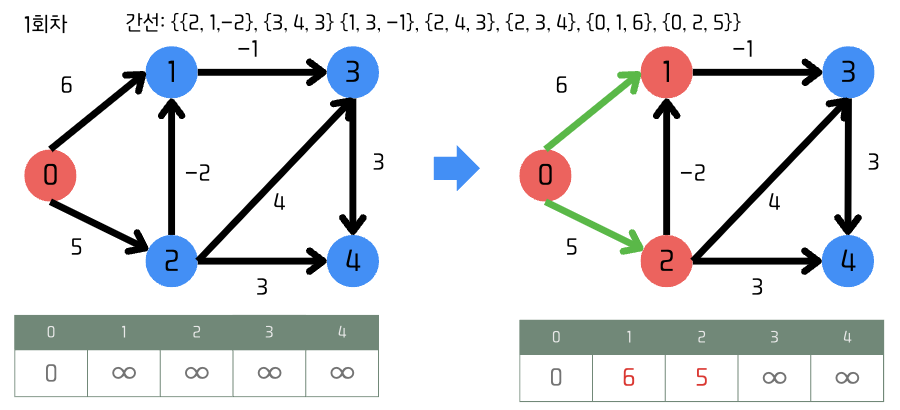
-
2회차

-
3회차
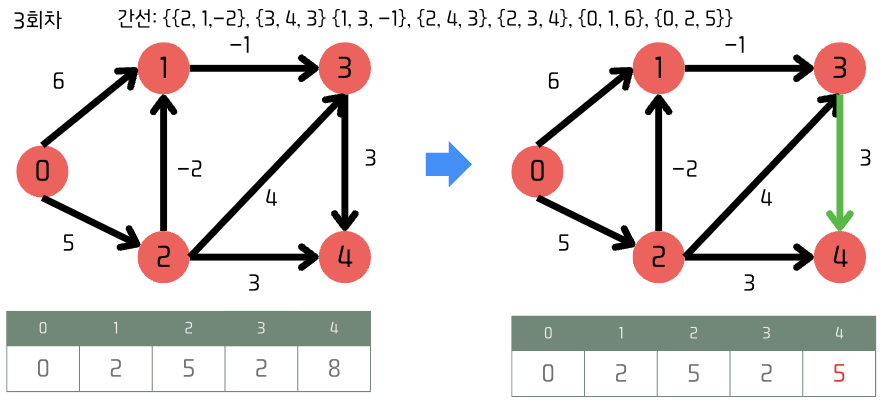
-
4회차(n-1) [탐색 종료]
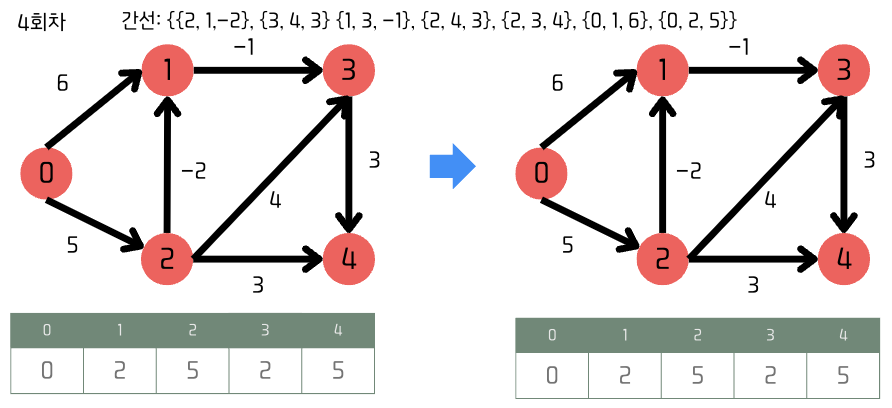
-
5회차(n) [루프 검증]
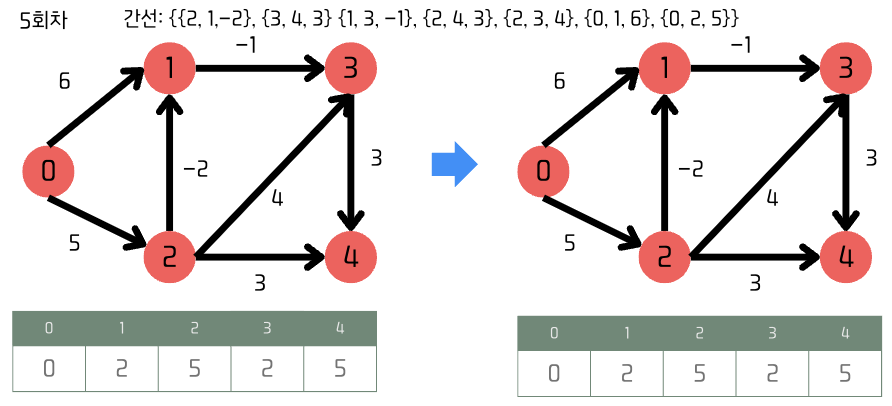
n-1번 반복하는 이유?
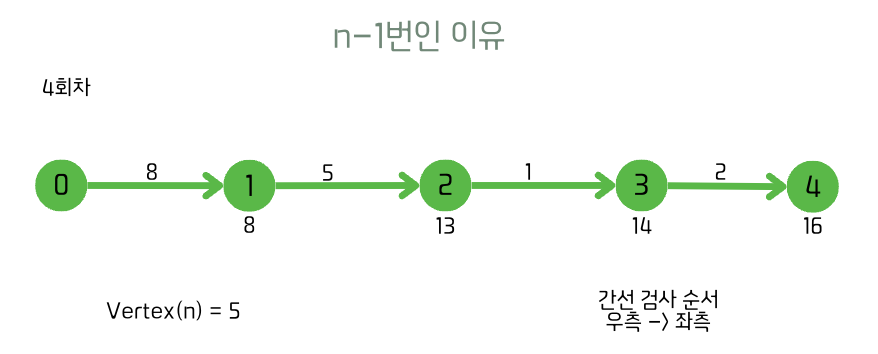
최악의 경로 탐색의 경우의 수는 위와 같은 단방향 그래프에서 시점의 반대 방향 간선부터 검사할 때이다.
이 경우 각 회차를 거듭할 때마다 왼쪽 간선부터 하나씩 최단 경로가 구해지는데 n-1번째 반복이 진행되면 최종 결과가 구해진다.
따라서 최악이 아닌 그래프들은 n-1번까지 반복하지 않아도 이미 결과값이 구해질 수 있지만, 알고리즘은 n-1번째 까지 진행해야 확신할 수 있으므로 결과가 미리 구해지는지 여부와 관계 없이 n-1번 반복은 반드시 진행된다.
n번 반복이 음수 사이클 검증인 이유?
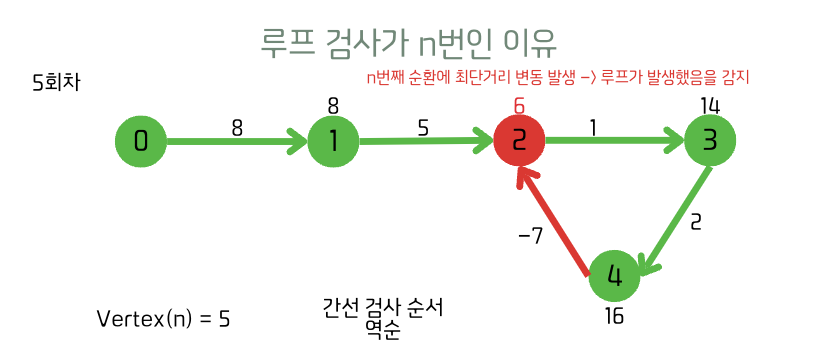
n-1번 Relaxation을 진행하고 최단경로가 정상적으로 정해지는 그래프라면, 이후 몇 번을 반복해도 결과 테이블이 갱신되지 않는다.
설사 사이클이 있다 하더라도, 사이클을 이루는 간선의 합이 음수가 아니면 갱신 원리에 따라 작은값이 아니기 때문에 반복이 거듭되어도 아무 변경 없이 계속 같은 결과를 유지한다.
하지만 만약 사이클을 이루는 간선의 합이 음수인 음수 간선 사이클이 발생한다면 n 번째부터 해당 사이클에 영향을 받는 정점부터 값이 계속해서 줄어들기 시작하여 무한히 비용을 줄일 수 있게 된다.
따라서 최악의 경우 최단경로를 구하는 n-1번째 반복이 끝나고나서 n번째 이후 반복부터 결과 테이블 값이 갱신되면 음수 간선 사이클이 발생했다고 알 수 있다.