Dijkstra

다익스트라 알고리즘

그리디 알고리즘과 동적 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘

그리디 알고리즘

문제를 해결할 때 각 단계에서 가장 최적인 선택을 하는 방법론.

매 순간 가장 좋은 선택을 함으로써 전체 문제의 최적해에 도달하려고 시도한다.

동적 프로그래밍

하나의 알고리즘을 부분으로 나누어 해결한 결과를 저장하여 더 큰 문제를 해결하는 알고리즘 설계 기법

장점

• 효율성

• 실시간 최단 경로 갱신

단점

• 음수 가중치 간선 처리 불가

• 코드 복잡성

사용 조건 및 활용처

• 양의 가중치를 가진 간선만 있는 경우

• 정적 환경

• 네트워크 라우팅

• GPS

선택된 최단거리를 재확인 하지 않는 이유

각 단계에서 그리디 알고리즘에 의해 최적의 선택을 했다고 가정하기 때문에 선택 후 해당 정점은 더 이상 변경이 필요없다고 판단하기 때문이다.

전체 간선의 가중치가 양수라면 각 정점에서 비용이 가장 낮은 간선이 최적의 선택이지만, 가중치가 음수인 간선이 존재하면 더 나은 경로가 발생할 가능성이 있다.

하지만 다익스트라는 이미 방문처리한 정점은 재방문 하지 않기 때문에 더 나은 경로로 갱신하지 못해 음의 가중치를 가진 간선을 처리하지 못한다.

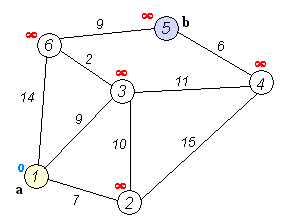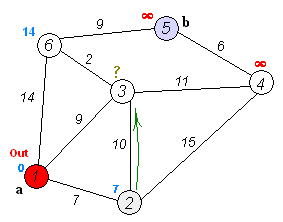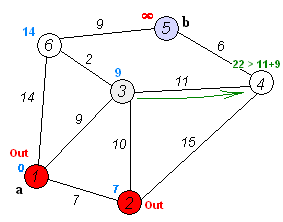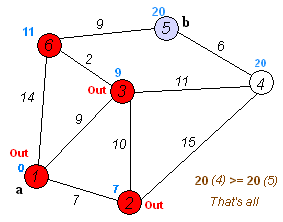
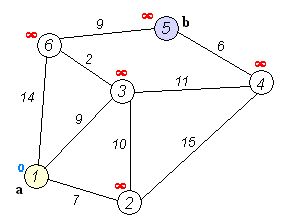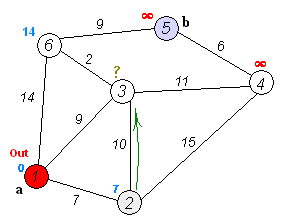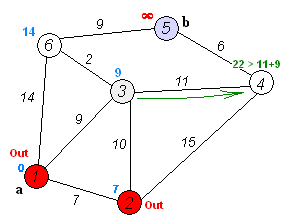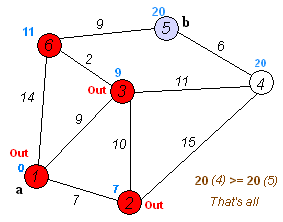
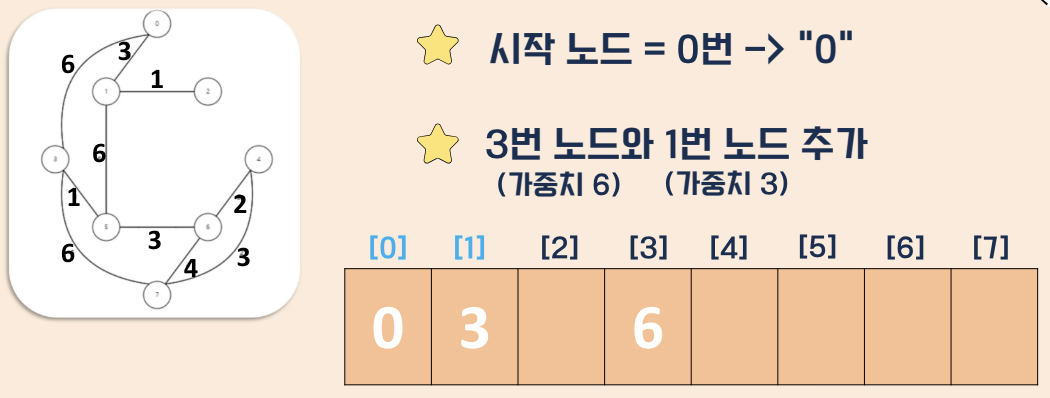
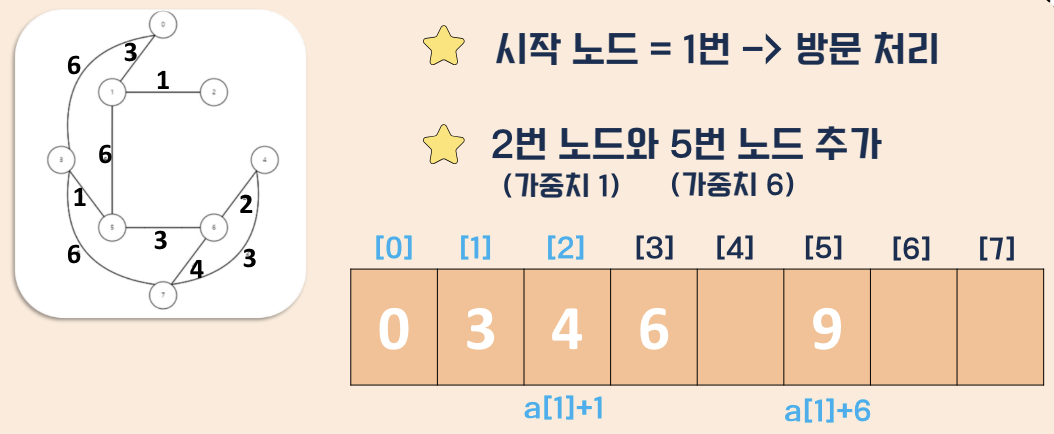
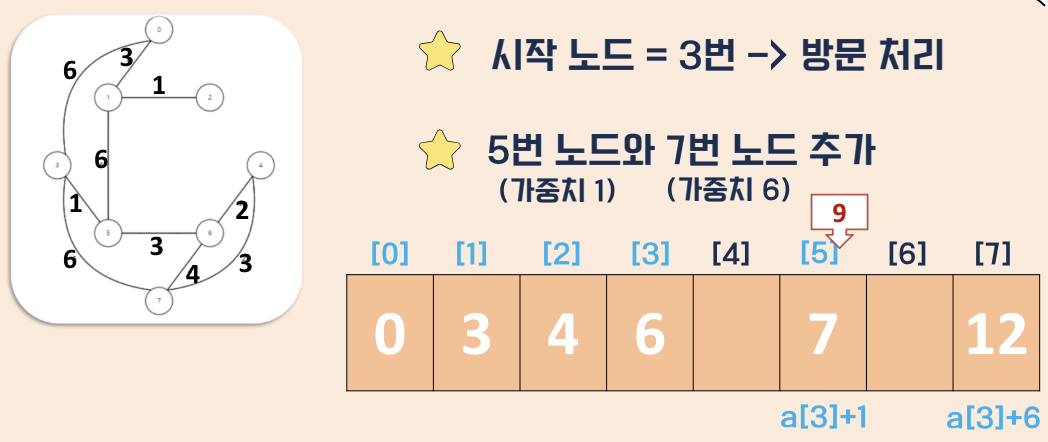
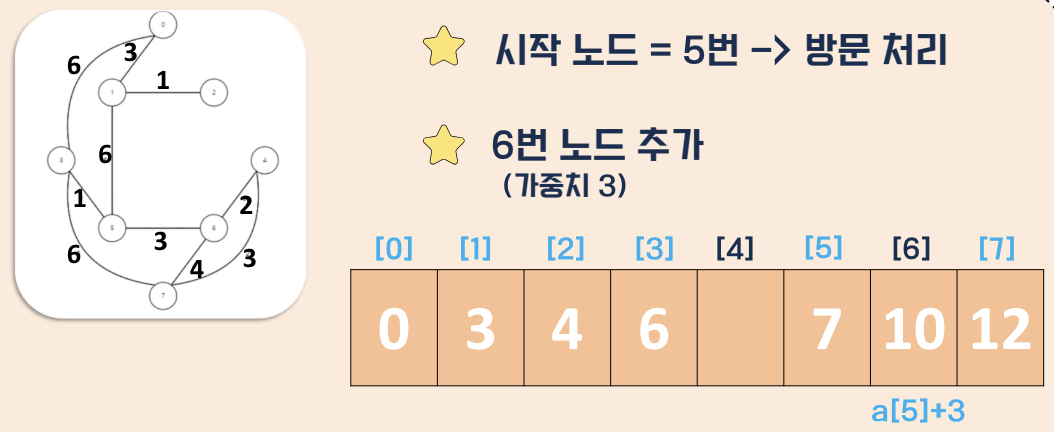
탐색 과정

1. 거리값 초기화
   
   
2. 시점부터 연결된 간선중 가중치가 가장 낮은 비용을 선택
   
   
3. 해당 간선과 연결된 정점을 방문처리
   
   
4. 다른 정점에 대해 반복

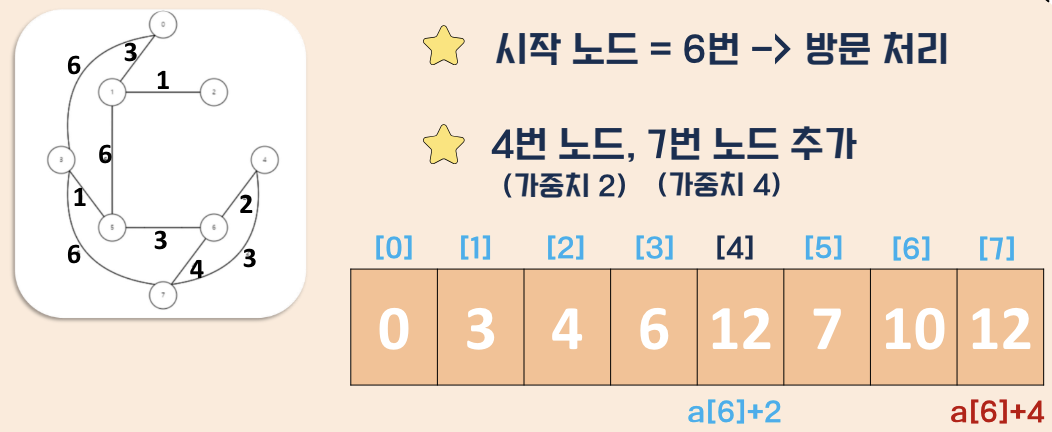
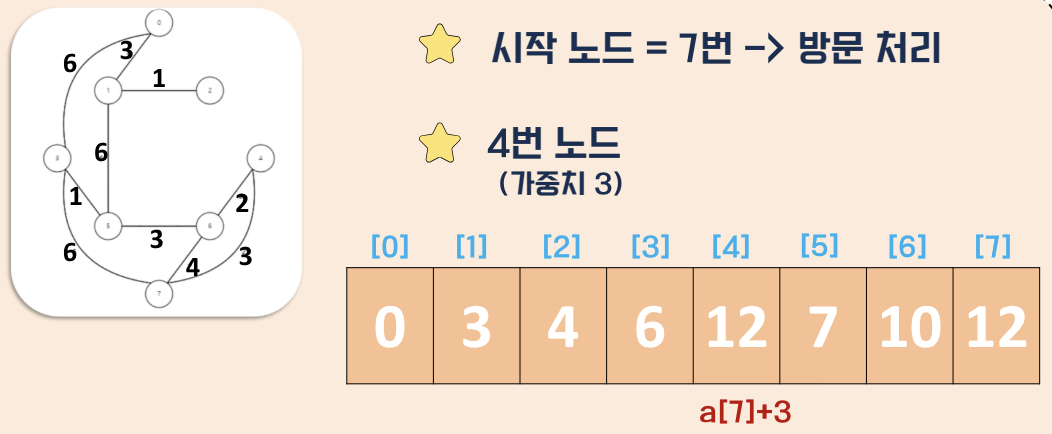
구현 방식별 특징

우선순위 큐 활용

• 최적의 시간 복잡도

  O(V^2) -> O((V+E)log V)로 향상됨

• 빠른 최소 거리 정점 선택

  알고리즘 성능 향상

• 동적 거리 갱신

  정점의 거리가 줄어들 때 우선 순위 큐에서 빠르게 재정렬되므로, 최단 경로를 효율적으로 탐색

인접행렬 활용

• 구현의 직관성

  배열 인덱싱을 통해 그래프를 쉽게 표현하고 다룰 수 있음

• 메모리 접근의 효율성

  메모리에 연속적으로 배치되어 있어 캐시 효율성이 높음

• 완전한 간선 정보 포함

  모든 정점 쌍 간의 간선 정보를 명확하게 포함하고 있음