가능한 모든 부분 문자열의 조합 구하기

LeetCode: 250215 Daily Question

2698. Find the Punishment Number of an Integer

Given a positive integer n, return the punishment number of n.
The punishment number of n is defined as the sum of the squares of all integers i such that:
1 <= i <= n
The decimal representation of i * i can be partitioned into contiguous substrings such that the sum of the integer values of these substrings equals i.

Example

Input: n = 10
Output: 182
Explanation: There are exactly 3 integers i in the range [1, 10] that satisfy the conditions in the statement:

• 1 since 1 * 1 = 1
• 9 since 9 * 9 = 81 and 81 can be partitioned into 8 and 1 with a sum equal to 8 + 1 == 9.
• 10 since 10 * 10 = 100 and 100 can be partitioned into 10 and 0 with a sum equal to 10 + 0 == 10.
  Hence, the punishment number of 10 is 1 + 81 + 100 = 182

leetcode official solution →

How I solved the problem?

우선 n의 제곱을 구해서 문자열로 만든다. 문자열을 쪼갠 후 조합을 해서 n과 같아지면 그 숫자는 punishment number이다.

내가 생각한 풀이는 다음과 같다.
주어진 문자열(숫자)로 가능한 모든 부분 문자열을 찾아서 n과 비교하면 되겠다. 가능한 모든 조합을 찾는 방법은?

=> 1 2 3, 12 3, 1 23, 123

간단하게 생각해 보면 3개의 문자열에서 나올 수 있는 경우의 수는 총 4가지이다. 문자열 사이마다 split 하는 막대기가 있다고 가정하고 그 막대기는 있을 수도 있고 없을 수도 있다. 즉, (문자열의 길이 - 1) 만큼 제곱을 하면 경우의 수를 알 수 있다.
But, 문제는 그래서 결국 n과 같은 조합이 있는지를 찾는 거다. 모든 조합을 구해서 비교하는 것보다 당연히 더 좋은 방법이 있겠지만 내가 푼 방법은 다음과 같다.

하지만!! 여기서 막혀서 구글링을 했다. 모든 경우의 수는 구하겠는데 어떻게 반복문을 돌면서 부분 문자열의 조합을 구할 수 있는지 감이 잡히지 않았다.🧐 구글링 결과 여러 방법이 있었지만 제일 간단해 보였던 방법은 비트마스킹을 활용하여 모든 경우의 수를 탐색하는 방법이었다.

왜 비트로 접근할까??? 우리는 모든 경우의 수를 구할 수는 있다. 그런데 어디를 먼저 끊어서 부분 문자열을 구해야 하는지, 기준을 어떻게 세워야 하는지 몰랐다. BUT!! 모든 경우의 수를 알고 그만큼 반복분을 돌면서 단순 i의 비트로 접근하게 되면 0이나 1 둘 중에 하나를 기준으로 잡아서 끊으면 된다! 😲

My code

var punishmentNumber = function (n) {
    let res = 0;

    for (let i = 1; i <= n; i++) {
        const sqaure = i * i;
        const numStr = sqaure.toString()
        const len = numStr.length;

        for (let j = 0; j < Math.pow(2, len - 1); j++) {
            let temp = [];
            let sum = 0;
            let part = "";

            for (let k = 0; k < len; k++) {
                part += numStr[k];

                if (((j >> k) & 1) || k === len - 1) {
                    temp.push(part);
                    part = "";
                }
            }

            sum = temp.reduce((a, b) => +a + +b)

            if (Number(sum) === i) {
                res += sqaure;
                break;
            }
        }
    }

    return res;
};

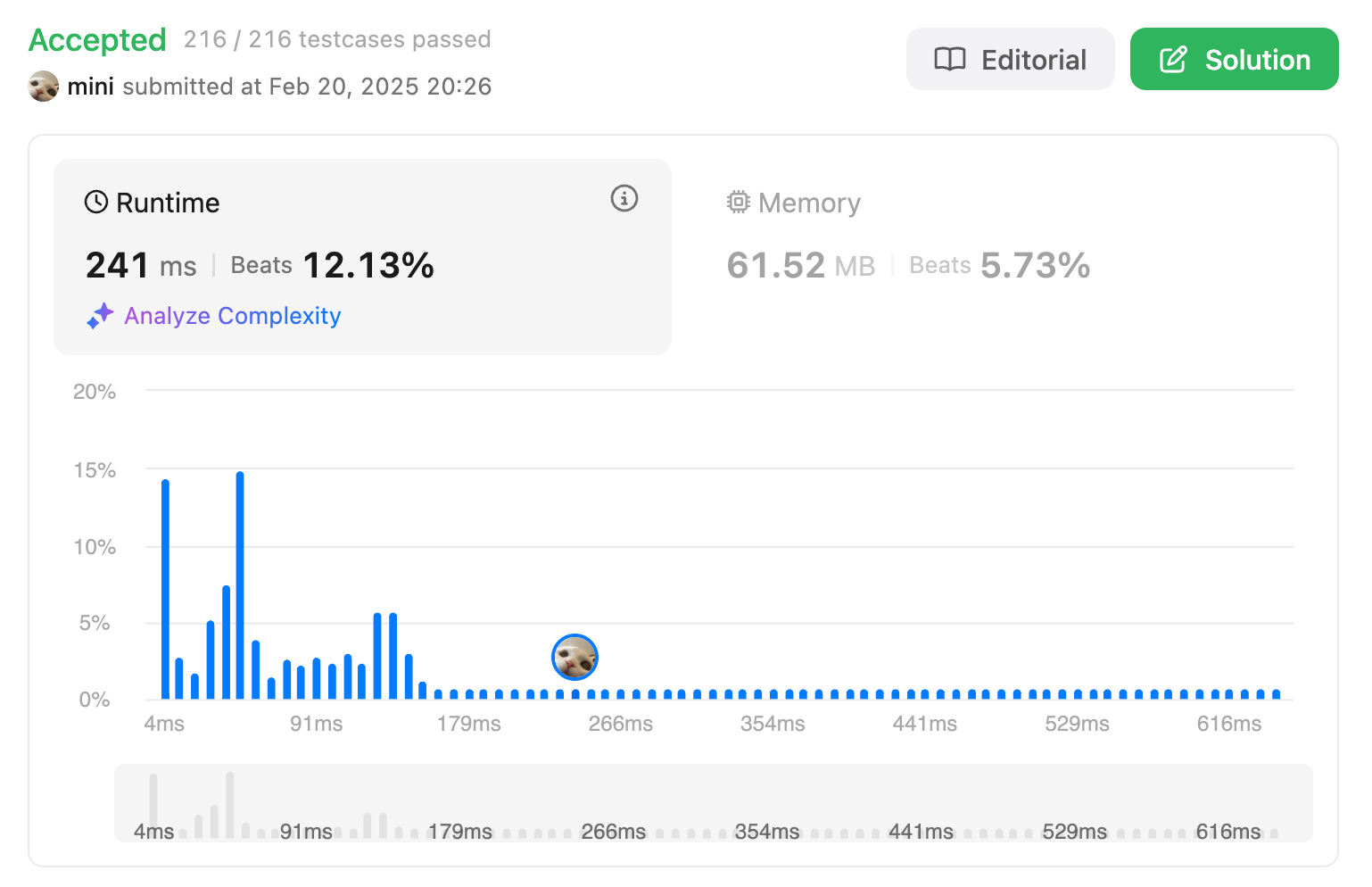통과는 했지만 runtime이 굉장하다..! 알고리즘에 도전하는 사람이 맞는건가?!싶다.

구글링을 했을 때 비트마스킹보다 더 좋은 방법들이 있었기에 더 괜찮은 해결방법에 무엇이 있는지 찾아보았다.

재귀적 백트래킹

릿코드에 올라온 여러 솔루션들을 참고했을때 '재귀적 백트래킹' 개념이 많이 보였다.
가능한 모든 경우의 수를 탐색하는 데 매우 유용하다고 한다. 간단한 개념은 다음과 같다.

[재귀]

함수가 자기 자신을 호출하는 기법

• 기본 아이디어: 큰 문제를 더 작은 하위 문제로 나눠서 해결하는 방식
• 기저 조건(Base Case): 재귀 호출을 멈추기 위한 조건을 반드시 설정해야 한다.

[백트래킹]

가능한 모든 선택지를 하나씩 시도해보면서, 만약 어떤 선택이 올바른 해답으로 이어지지 않는다고 판단되면, 그 선택을 취소(되돌리기)하고 다른 선택지를 시도하는 방법

• 탐색: 예를 들어 미로 찾기를 생각해보면, 한 방향으로 쭉 나아가다가 막다른 길에 다다르면 이전 갈림길로 돌아가 다른 경로를 시도하는 방식과 유사
• 가지치기(Pruning): 불필요한 경로를 미리 포기함으로써 탐색 효율을 높일 수 있다.

[재귀적 백트래킹]

위 두 가지 기법을 결합한 것이 바로 재귀적 백트래킹

1. 선택: 문제를 해결하기 위해 가능한 모든 선택지 중 하나를 선택
2. 재귀 호출: 선택한 후, 남은 문제에 대해 같은 방법을 재귀적으로 적용
3. 검증: 만약 현재 선택이 올바른 해답으로 이어지지 않는다고 판단되면, 되돌리기(백트랙) 하여 다른 선택지를 시도
4. 완성: 모든 선택지를 시도해서 조건에 맞는 해답을 찾으면, 그 결과를 반환

코드 예시 (재귀적 백트래킹을 활용한 문자열 분할)

function getPartitionsRecursive(str) {
  const result = [];
  
  function backtrack(start, current) {
    // 문자열의 끝에 도달하면 하나의 분할 조합 완성
    if (start === str.length) {
      result.push([...current]);
      return;
    }
    
    // 가능한 모든 분할 위치 시도
    for (let end = start + 1; end <= str.length; end++) {
      // 현재 부분 문자열 선택
      current.push(str.slice(start, end));
      // 남은 문자열에 대해 재귀 호출
      backtrack(end, current);
      // 잘못된 경로였으면 마지막 선택을 되돌림 (백트래킹)
      current.pop();
    }
  }
  
  backtrack(0, []);
  return result;
}

console.log(getPartitionsRecursive("123"));
// [ [ '1', '2', '3' ], [ '1', '23' ], [ '12', '3' ], [ '123' ] ]

((참고로 해당 코드는 단순히 재귀적 백트래킹의 예제 코드로 시간, 공간 복잡도가 좋은 코드라고 볼 수는 없다. slice 메서드는 새로운 문자열 객체를 생성하는데 만약 재귀 호출이 매우 빈번하게 발생한다면, 이 과정에서 많은 메모리 할당이 일어나게 되기 때문이다. 예제는 예제일 뿐))

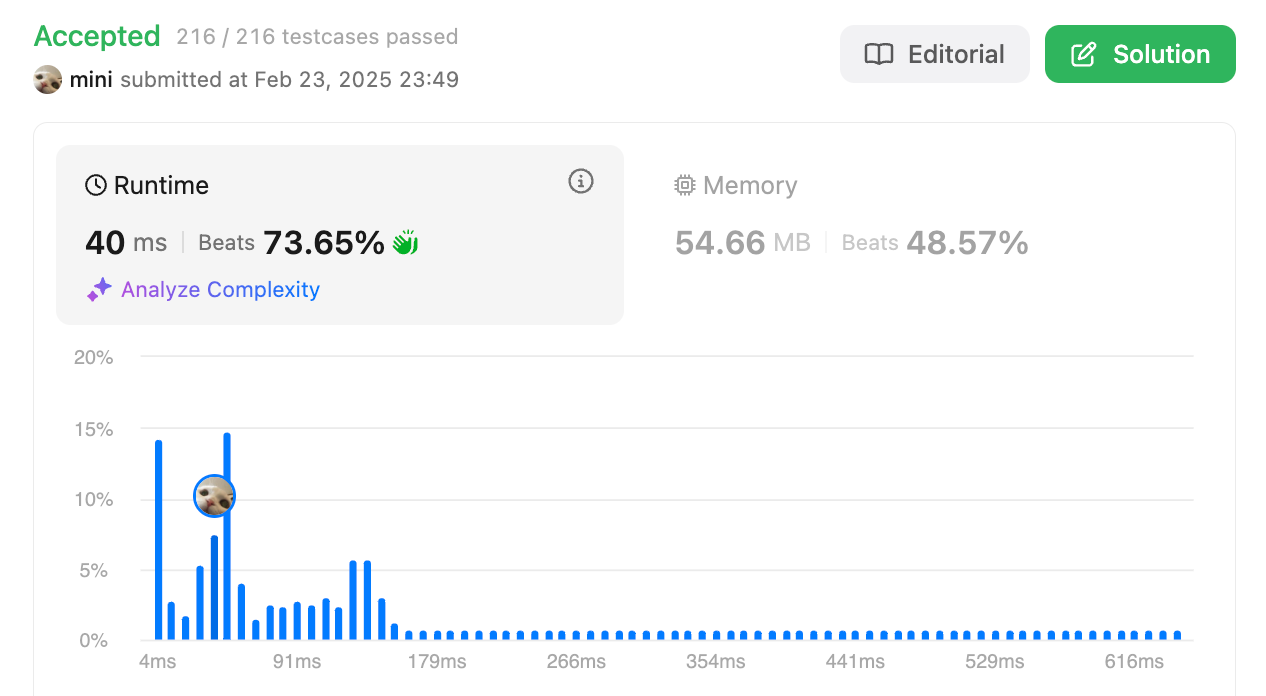
최종 코드

Solution link →

var punishmentNumber = function (n) {
    let sum = 0;

    function canPartition(num, index, target) {
        if (index === num.length) {
            return target === 0;
        }

        let curr = 0;
        for (let i = index; i < num.length; i++) {
            curr = curr * 10 + Number(num[i]);
            if (curr > target) break;
            if (canPartition(num, i + 1, target - curr)) return true;
        }
        return false;
    }

    for (let i = 1; i <= n; i++) {
        if (canPartition(String(i * i), 0, i)) {
            sum += (i * i);
        }
    }
    return sum;
};