1. 문제설명
문제 설명
매운 것을 좋아하는 Leo는 모든 음식의 스코빌 지수를 K 이상으로 만들고 싶습니다. 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 Leo는 스코빌 지수가 가장 낮은 두 개의 음식을 아래와 같이 특별한 방법으로 섞어 새로운 음식을 만듭니다.
섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)
Leo는 모든 음식의 스코빌 지수가 K 이상이 될 때까지 반복하여 섞습니다.
Leo가 가진 음식의 스코빌 지수를 담은 배열 scoville과 원하는 스코빌 지수 K가 주어질 때, 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 섞어야 하는 최소 횟수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
scoville의 길이는 2 이상 1,000,000 이하입니다.
K는 0 이상 1,000,000,000 이하입니다.
scoville의 원소는 각각 0 이상 1,000,000 이하입니다.
모든 음식의 스코빌 지수를 K 이상으로 만들 수 없는 경우에는 -1을 return 합니다.
입출력 예
----------------------------------
scoville | K | return
----------------------------------
[1, 2, 3, 9, 10, 12] | 7 | 2
----------------------------------
입출력 예 설명
스코빌 지수가 1인 음식과 2인 음식을 섞으면 음식의 스코빌 지수가 아래와 같이 됩니다.
새로운 음식의 스코빌 지수 = 1 + (2 * 2) = 5
가진 음식의 스코빌 지수 = [5, 3, 9, 10, 12]
스코빌 지수가 3인 음식과 5인 음식을 섞으면 음식의 스코빌 지수가 아래와 같이 됩니다.
새로운 음식의 스코빌 지수 = 3 + (5 * 2) = 13
가진 음식의 스코빌 지수 = [13, 9, 10, 12]
모든 음식의 스코빌 지수가 7 이상이 되었고 이때 섞은 횟수는 2회입니다.2. 나의 풀이
2-1) 문제 정의와 나의 풀이
<문제 정의>
- scoville 배열을
- 오름차순으로 정렬한 배열에서
- 첫 요소가 K보다 작은 경우 다음 과정을 반복하기
- 가장 작은 요소(x) + 두 번째로 작은 요소(y)*2를
- scoville 배열에 추가하기
- 만약 과정 중 scoville의 가장 작은 요소가 K보다 크다면 반복한 횟수 출력
- scoville의 요소가 하나가 되었고, 그 값이 K보다 작다면 -1 출력
function solution(scoville, K) {
let count = 0;
while (scoville.length > 1) {
// scoville 배열 오름차순 정렬
scoville.sort((a, b) => a - b);
// 가장 작은 요소가 K보다 크다면 반복횟수 출력
if (scoville[0] >= K) {
return count;
}
// 가장 작은 요소(x)와 두 번째 작은 요소(y)로 다음 수식으로 구한 값을 scoville 배열에 추가
let x = scoville.shift();
let y = scoville.shift();
let newScov = x + y*2
scoville.push(newScov);
// 반복 횟수 + 1
count++;
}
// scoville 배열의 요소가 하나만 남았을 때, 그 값이 K보다 크다면 반복횟수 출력하고 아닌 경우 -1 출력
return scoville[0] >= K ? count : -1;
}2-2) 나의 풀이 채점결과

2-3) 문제 재정의와 두 번째 나의 풀이
<문제 재정의>
- 정확성 테스트는 모두 통과했으나 효율성에서 0점을 받았다. => 단순 구현문제가 아닌 특정 알고리즘으로 풀어야 한다.
(위에서 사용한Array.shift()의 시간 복잡도가 O(n)이어서 정렬을 내림차순으로 바꾸고 시간복잡도가 O(1)인Array.pop()을 적용했지만 통과되지 않았다.)- 이 문제의 핵심은 정렬의 시간복잡도를 줄이는 것이다.
- 해당 문제의 가장 적합한 알고리즘은 최소 힙(min-Heap)이라고 한다. 자바스크립트에서는 슬프지만 힙을 직접 만들어야 한다. => 요령은 없다.
- 하지만, 문제에 따라 효율적인 구조는 바뀔 수 있으므로 기본 개념만 배우고 응용하자!
- 힙은 요소를 추가하거나 삭제할 때 동시에 정렬을 한다. 이때 이진트리 구조를 통해 비교하는 정렬 방식으로 O(logN)의 시간복잡도를 가지는 구조이다.
function solution(scoville, K) {
let count = 0;
const heap = new MinHeap();
scoville.forEach(value => heap.push(value));
while (heap.size() > 1 && heap.peek() < K) {
let x = heap.pop();
let y = heap.pop();
let newScov = x + y * 2;
heap.push(newScov);
count++;
}
if (heap.peek() < K) {
return -1;
}
return count;
}
class MinHeap {
constructor() {
this.heap = [];
}
size() {
return this.heap.length;
}
isEmpty() {
return this.size() === 0;
}
peek() {
if (this.isEmpty()) {
return null;
}
return this.heap[0];
}
push(value) {
this.heap.push(value);
this.bubbleUp(this.size() - 1);
}
pop() {
if (this.isEmpty()) {
return null;
}
const min = this.peek();
const last = this.heap.pop();
if (!this.isEmpty()) {
this.heap[0] = last;
this.bubbleDown(0);
}
return min;
}
bubbleUp(index) {
let currentIdx = index;
while (currentIdx > 0) {
const parentIdx = Math.floor((currentIdx - 1) / 2);
if (this.heap[parentIdx] <= this.heap[currentIdx]) {
break;
}
this.swap(parentIdx, currentIdx);
currentIdx = parentIdx;
}
}
bubbleDown(index) {
let currentIdx = index;
while (true) {
let leftIdx = currentIdx * 2 + 1;
let rightIdx = currentIdx * 2 + 2;
let smallest = currentIdx;
if (leftIdx < this.size() && this.heap[leftIdx] < this.heap[smallest]) {
smallest = leftIdx;
}
if (rightIdx < this.size() && this.heap[rightIdx] < this.heap[smallest]) {
smallest = rightIdx;
}
if (smallest !== currentIdx) {
this.swap(currentIdx, smallest);
currentIdx = smallest;
} else {
break;
}
}
}
swap(p, q) {
[this.heap[p], this.heap[q]] = [this.heap[q], this.heap[p]];
}
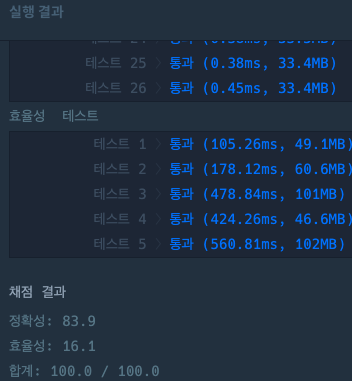
}2-4) 두 번째 풀이 채점 결과
3. 다른 사람의 풀이
3-1) 다른 사람의 풀이
class MinHeap {
constructor() {
this.heap = [];
}
size() {
return this.heap.length;
}
swap(idx1, idx2){
[this.heap[idx1], this.heap[idx2]] = [this.heap[idx2], this.heap[idx1]];
return this.heap;
}
getParentIdx(childIdx){
return Math.floor((childIdx-1) / 2);
}
getLeftChildIdx(parentIdx){
return parentIdx*2 + 1;
}
getRightChildIdx(parentIdx){
return parentIdx*2 + 2;
}
heappop(){
const heapSize = this.size();
if (!heapSize) return null;
if (heapSize === 1) return this.heap.pop();
const value = this.heap[0];
this.heap[0] = this.heap.pop();
this.bubbledown();
return value;
}
heappush(value){
this.heap.push(value);
this.bubbleup();
return this.heap;
}
bubbleup() {
let child = this.size()-1;
let parent = this.getParentIdx(child);
while(this.heap[child] < this.heap[parent]){
this.swap(child, parent);
child = parent;
parent = this.getParentIdx(parent);
}
}
bubbledown() {
let parent = 0;
let leftChild = this.getLeftChildIdx(parent);
let rightChild = this.getRightChildIdx(parent);
while((leftChild <= this.size()-1 && this.heap[leftChild] < this.heap[parent]) || (rightChild <= this.size()-1 && this.heap[rightChild] < this.heap[parent])){
if (rightChild <= this.size()-1 && this.heap[leftChild] > this.heap[rightChild]){
this.swap(parent, rightChild);
parent = rightChild;
}else {
this.swap(parent, leftChild);
parent = leftChild;
}
leftChild = this.getLeftChildIdx(parent);
rightChild = this.getRightChildIdx(parent);
}
}
}
function solution(scoville, K) {
let count = 0;
const heap = new MinHeap();
scoville.forEach(el => heap.heappush(el));
while(heap.heap[0] < K && heap.size() > 1){
count++;
heap.heappush(heap.heappop() + heap.heappop()*2);
}
return heap.heap[0] >= K ? count : -1;
}3-2) 다른 사람의 풀이 채점 결과

4. 느낀 점
<나의 풀이와 달랐던 점>
- 두 번째 풀이에선 2시간을 넘게 풀게 되었다. 이는 너무 비효율적이라서 Chat-GPT 선생님께 질문하고 정석적인 답변을 얻었다.
- Chat-GPT 선생님과 다른 사람의 풀이를 하나씩 뜯어보면서 나의 머리 속으로 각인시키는 시간을 가지고자 한다.
- 힙(Heap)이라는 구조를 알게 되었다. 기존에 삽입, 삭제한 뒤 다시 정렬하는 과정(O(N))에서 이진트리 구조를 활용하여 새롭게 얻게 된 값(newScov)을 기존 배열의 요소들과 logN만큼만 비교하여 정렬하는 효율적인 방식이다.

