- 선입선출 FIFO(first in first out) ↔ LIFO(last in last out) 스택
- 시간복잡도 enqueue(맨 뒤에 데이터 추가), dequeue(맨 앞에 데이터 추출) 모두 O(1)
- 활용 예시 Cache 구현, 프로세스 관리, 너비우선탐색(BFS) 등
구현 방식
- Array-Based queue

- enqueue, dequeue 과정에서 남는 메모리가 생기므로(앞에는 계속 빈공간이 생기고 뒤로 계속 배열이 커진다) 낭비를 줄이기 위해 주로 Circular queue 형식으로 구현한다.
- enqueue가 계속 발생하면 fixed size를 넘어서므로 dynamic array와 같은 방법으로 size를 확장시켜야 한다.
- 그럼에도 enqueue의 시간복잡도는 (amortized)O(1)을 유지 할 수 있다.
2. List-Base queue
- 재할당이나 메모리 낭비의 걱정을 할 필요 없다.
- enqueue는 단순히 singly-linked list 에서 append 하는 것으로 구현, 시간복잡도 O(1)
- deque는 맨 앞의 원소를 삭제하고 fist head를 변경하므로 연산도 O(1)
3. 두가지 구현 모두 O(1)의 시간복잡도를 갖는다.
- 전반적 performance는 배열 구현이 더 좋지만, worst case의 경우(resize)에는 훨씬 더 느리다.
- 리스트 구현은 enqueue 할때 마다 memory allocation을 해야 하기 때문에 전반적 runtime이 느릴 수 있다.
확장, 활용
- deque (덱)
- 양쪽에서 enqueue, dequeue 가능 (double-ended queue)
- priority queue
- 시간순서가 아닌 우선순위가 높은 순서로 dequeue 할 수 있다.
- 하나의 자원을 공유하는 프린터, CPU task scheduling, Cache 구현, 너비 우선탐색(BFS) 등으로 활용한다.
Circular Queue
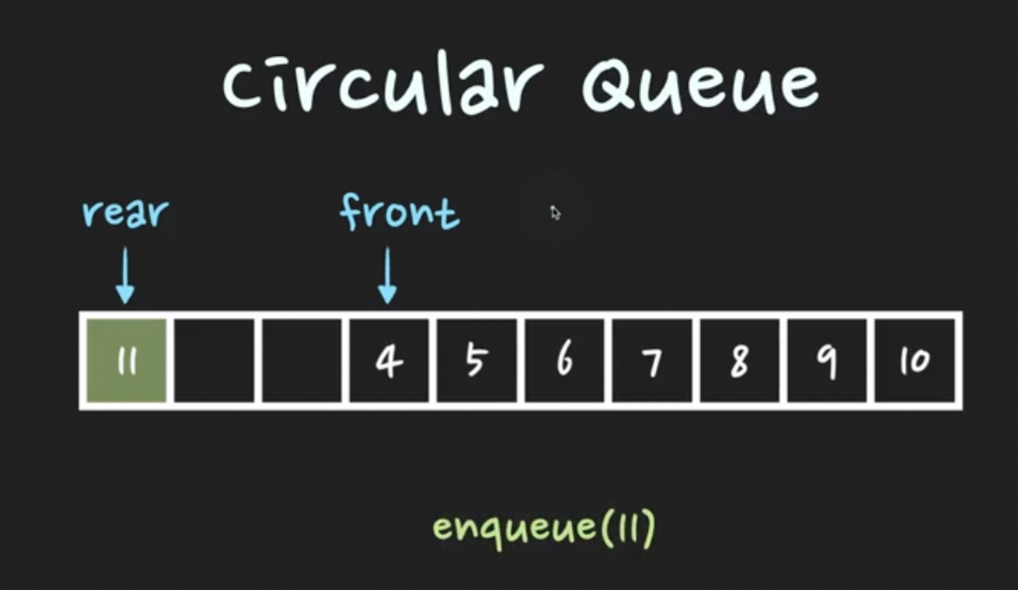
- 배열의 뒷부분에 더이상 자리가 없을때 비어있는 앞부분에 enqueue → 원형처럼 순환
priority queue
- 큐와 다르게 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나온다.
- 시간복잡도
- Queue : enqueue(), dequeue() → O(1)
- priority queue : push(), pop() → O(logn)
- heap tree의 높이는 logN
- push(), pop() 했을때 swap하는 과정이 최대 logN번 반복
- 구현
- Heap은 그 자체로 우선순위큐의 구현과 일치한다. (이진완전트리 구조)
- tree가 그려져 있는 상태에서 최대힙, 최소힙의 삽입과 삭제시에 어떻게 node가 삭제되거 연결이 변경되는지의 과정을 그려서 설명할 수 있으면 좋다.
- max heap의 조건 : 부모노드 ≥ 자식노드 (모든 노드에 한하여) ⇒ 루트 노드에 가장 큰 값이 저장된다.
- min heap의 조건 : 부모노드 ≤ 자식노드 ⇒ 루트 노드에 가장 작은 값이 저장된다.
Heap
- 트리는 보통 linked list로 구현하지만
- 새로운 노드를 힙의 ‘마지막 위치’에 추가해야 하는데, 이때 array 기반으로 구현해야 이 과정이 수월해지므로 힙은 트리임에도 array 기반으로 구현한다.
- 구현의 편의를 위해 array의 0번째 인덱스는 사용하지 않는다.
- 원래 트리는 포인터로 연결하여 부모, 자식 간의 관계를 정의하지만, 완전이진트리의 특성에 의해 배열의 인덱스 만으로도 부모, 자식 관계를 알 수 있다.
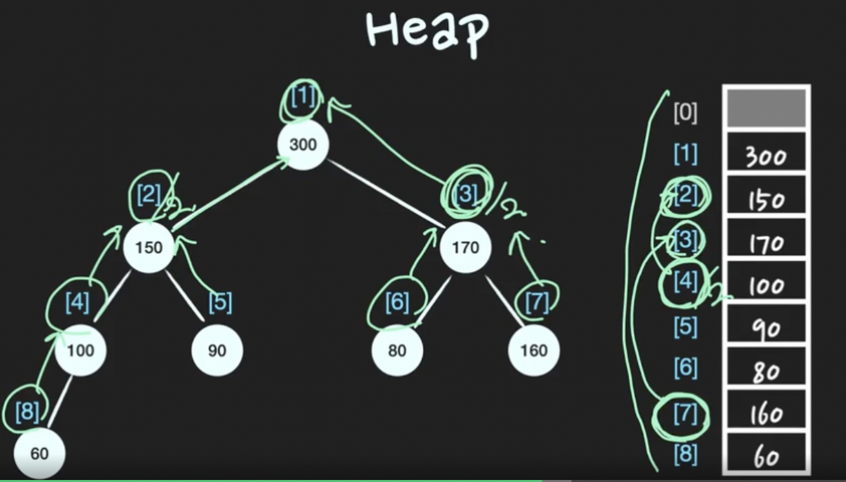
- n번째 노드의 왼쪽 자식 노드의 인덱스 = 2n
- n번째 노드의 오른쪽 자식 노드의 인덱스 = 2n + 1
- n번째 노드의 부모 노드의 인덱스 = n/2
Max heap
<push(190)>
- heap의 맨 마지막 인덱스에 값 저장
- 부모 노드의 값이 더 작다면 swap
- 부모 노드의 값이 더 클때까지 계속 swap ⇒ push 완료, O(logn)
<pop()>
- 첫번째 인덱스에 저장되어 있는 값 pop
- 마지막 인덱스에 저장되어 있는 값을 top으로 옮기기
- 자식노드가 더 작은지 확인 후 자식노드 중 더 큰 값과 swap
- 반복 ⇒ pop 완료, O(logn)