Stack으로 Queue, Queue로 Stack 구현하기

LIFO

• 양쪽이 아니라 한쪽으로만 들어가고 나온다.
• 시간 순서상 가장 최근에 추가한 데이터가 가장 먼저 나온다.

push & pop

• push, pop 모두 맨뒤(top)의 데이터를 추가/삭제 하는 형식으로 구현되므로 둘다 O(1)

활용

• 재귀적 특성이 있어 프로그램을 개발할때 자주 쓰이는 자료구조이다.
• 활용 예시로는 call stack, 후위 표기법 연산, 괄호 유효성 검사, 웹 브라우저 방문기록(뒤로가기), 깊이우선탐색(DFS) 등이 있다.

Stack 두개로 Queue 구현하기

• 이런 문제는 답이 다양하므로 풀이를 외우기 보단 접근 방식을 주의깊게 볼 것
  

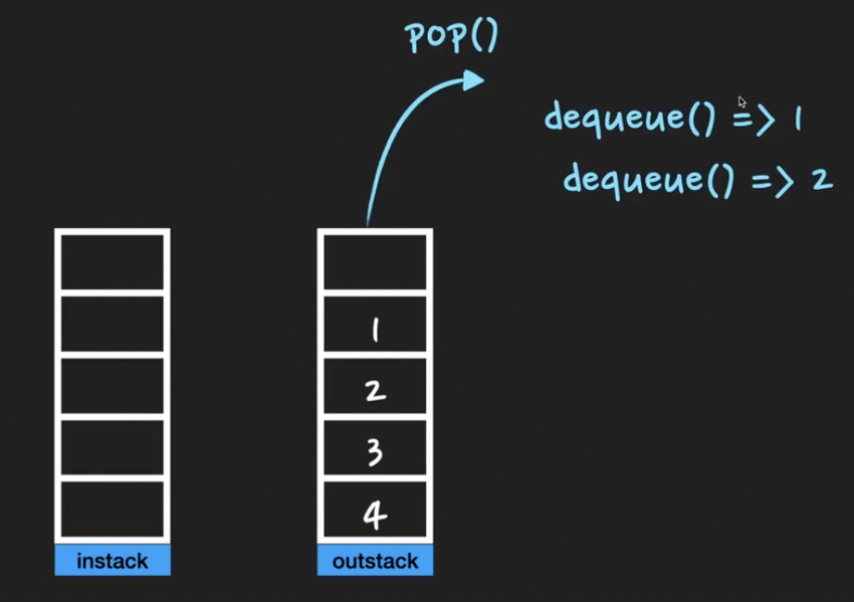
1. instack에 push() 하여 enqueue (이미 원소 있다면 생략 가능)
   • push() 한번만 하면 되기 때문에 시간복잡도 O(1)
2. instack에서 pop() 하여 outstack에 push() 한 뒤
3. outstack() 에서 pop() 하여 dequeue
   • worst case로 outstack이 비어있는 경우, instack의 n개의 데이터를 pop(), push() 두번 하므로 2*n 번의 operation이 실행 ⇒ O(n)
   • outstack이 비어있지 않는 경우, pop()만 하므로 O(1)
   • ⇒ 이를 종합했을때 결과적으로 enqueue, dequeue 모두 O(1)

Queue 두개를 이용하여 Stack 구현하기

<push()>

• = enqueue()로 구현
• O(1)

<pop()>

• pop() 진행할 데이터 제회한 모든 데이터를 다른 queue에 옮기기 (dequeue(), enqueue())
• q1에 저장되어 있는 n개의 원소중에 n-1개를 q2로 옮겨야 하므로 O(n)

1. q1에 4만 남기고 1, 2, 3을 dequeue() 해서 q2에 enqueue()
2. q1 에서 4를 dequeue()
3. 다음 pop()을 위해 q1, q2의 이름 바꾸기
4. 3을 제외한 1, 2를 q2에 옮긴 후 3 dequeue()