시간 측정
- 입력크기에 대해 어떠한 알고리즘이 실행되는데 걸리는 시간
- 하드웨어 사양에 따라 시간이 달라지고, 하나의 컴퓨터에서도 측정할때마다의 cpu, ram 등의 상태에 따라 시간이 다르게 측정된다.
long beforeTime = System.currentTimeMillis(); int sum = 0; for (int i = 0; i < 1000000; i++) { for (int j = 0; j < 50000; j++) { sum += i*j; } } long afterTime = System.currentTimeMillis(); long secDiffTime = (afterTime - beforeTime)/1000; System.out.println("시간차이(m) : "+secDiffTime);
- 하드웨어 사양에 따라 시간이 달라지고, 하나의 컴퓨터에서도 측정할때마다의 cpu, ram 등의 상태에 따라 시간이 다르게 측정된다.
반복 횟수 측정
- ⇒ 주요로직의 반복횟수를 중점으로 측정된다.
if(true) cout << k << '\n';이10*n^+ n번 반복된다. (입력크기 n)for(int i = 0; i < 10; i++){ for(int j =0; j < n; j++){ for(int k = 0; k < n; k++){ if(true) cout << k << '\n'; } } } for(int i = 0; i < n; i++){ if(true) cout << i << '\n'; }
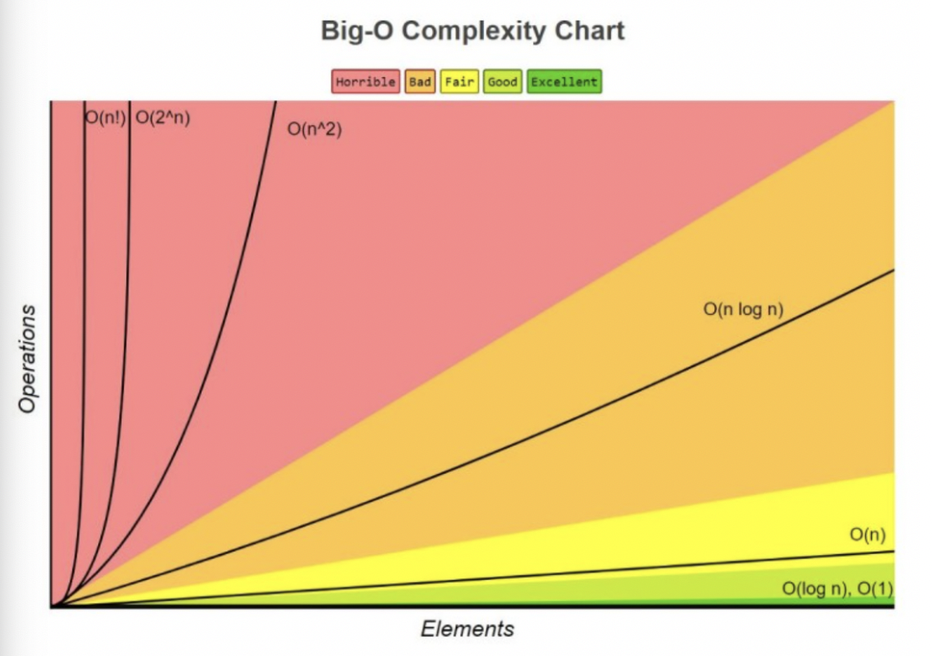
빅오표기법
- 복잡도에 가장 영향을 많이 끼치는 항의 상수인자를 빼고 나머지 항을 없애는 기법
- “영향을 많이 끼치는” = 증가속도(기울기)가 더 빠른 항 (n^ > n)
- 1, 3, 9, 12, … < 1, 9, 81, 144, …
10n^+n⇒O(n^)
- 증가속도가 더 빠른 항
- n! > 2^n > n^2 > n log n > n > log n > 1
n!+2^n이라면O(n!)
상수시간 시간복잡도 O(1)
- 입력크기와 상관없이 일정한 시간복잡도를 가지는 것으로, O(1)의 시간 복잡도를 쓴다.
// 1. 입출력 // cin, cout, scanf, printf for(int i = 0; i < 10; i++){ for(int j =0; j < n; j++){ for(int k = 0; k < n; k++){ if(true) cout << k << '\n'; // 이 부분은 O(1) (입출력) } } } n = 100 >> 10000000000 // 해도 입력크기와 상관없으므로 for(int i = 0; i < n; i++){ if(true) cout << i << '\n'; } // 2. 곱하기, 나누기, 나머지연산, 빼기 등 a[2] *= 2; // 3. 간단한 비교 if문 if(a[2] == 2) // 4. 배열의 인덱스 참조 int a[3] = {1, 2, 3}; int b = a[2];
상수시간 연산의 복잡도 계산하기
cnt 디버깅 하기 → 손코딩 → 그림
1. 사각형
#include<bits/stdc++.h>
using namespace std;
int n, cnt;
int main(){
cin >> n;
int a = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
a += i + j; // 상수시간 이므로 얼마만큼 반복되는지가 척도
}
}
cout << a << '\n';
cout << "cnt : " << cnt << '\n'; // 반복 횟수 세기(디버깅)
return 0;
}
/*
n 3 4 5 6
cnt 3 6 10 15
<손코딩>
i = 1 -> j = 0
2 0,1
3 0,1,2
4 0,1,2,3
=> 그림으로 그려보자
*/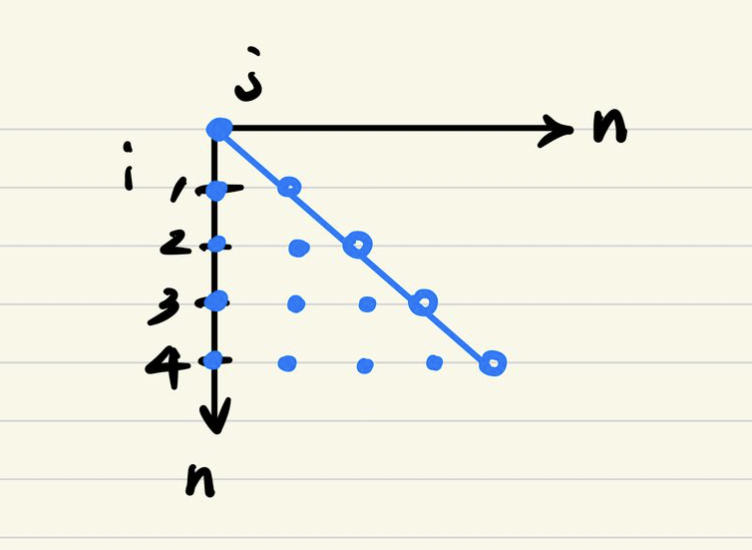
- 반복횟수 = 사각형의 넓이 = 격자점의 개수 →
n^/2 - j가 i를 포함하지 않으므로
(n^-n)/2= cnt O(n^)
2. 입력값 2개
#include<bits/stdc++.h>
using namespace std;
int N, M;
void solve(int N, int M){
int a = 1;
for (int i = 0; i < N; i++) {
a *= i;
}
for (int j = 0; j < M; j++) {
a *= j;
}
cout << a << "\n";
}
int main(){
cin >> N >> M;
solve(N, M);
return 0;
}
/*
for (int i = 0; i < N; i++) {
a *= i;
for (int j = 0; j < M; j++) {
a *= j;
}
}
이라면 nm
*/
/*
for (int i = 0; i < N; i++) {
a *= i;
for (int j = 0; j < N; j++) {
a *= j;
}
}
for (int i = 0; i < N; i++) {}
for (int i = 0; i < M; i++) {
a *= i;
for (int j = 0; j < M; j++) {
a *= j;
}
}
for (int i = 0; i < M; i++) {}
이라면 n^+n+m^+m
*/n+mn^+n+m^+m⇒O(n^+m^)
3. 재귀함수
#include<bits/stdc++.h>
using namespace std;
int n, a[1004], cnt;
int go(int l, int r){
cnt++; // 디버깅
if(l == r) return a[l];
int mid = (l + r) / 2; // 상수시간 복잡도
int sum = go(l, mid) + go(mid + 1, r); // 상수시간 복잡도
return sum;
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
a[i - 1] = i;
}
int sum = go(0, n - 1);
cout << sum << '\n';
cout << "cnt : " << cnt << "\n"; // 디버깅
}
/*
n = 5 -> cnt = 9
n = 10 -> cnt = 19
n = 20 -> cnt = 39
=> 2n-1
*/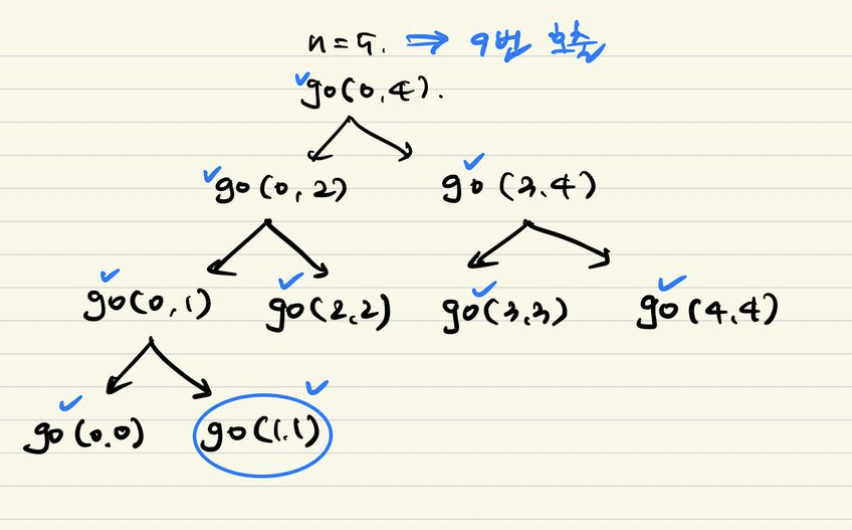
O(n)
4. 로그
#include<bits/stdc++.h>
using namespace std;
int N, cnt;
void solve(int N){
int a = 0, i = N;
while (i > 0) {
a += i;
i /= 2;
cnt++;
}
cout << a << '\n';
cout << cnt << '\n';
}
int main(){
cin >> N;
solve(N);
return 0;
/*
n = 32 -> cnt = 6
16 5
8 4
=> (log2 n) + 1
*/- 로그는 지수 함수의 역함수이다. 어떤 수를 나타내기 위해 고정된 밑을 몇 번 곱해야 하는지를 나타낸다.
- log2 32 = log2 2^5 = 5
- 2(밑)를 5번 곱하면 32
- 32 ↔ 16 ↔ 8 ↔ 4 ↔ 2 ↔ 1 (나누는 횟수와 곱하는 횟수가 같다)
O(log2 n)
5. 등비수열의 합
#include<bits/stdc++.h>
using namespace std;
int N, cnt;
void go(int N){
cnt++;
cout << cnt << '\n'; // 재귀 함수의 메인 로직
if(N == 0) return;
for(int i = 0; i < 3; i++){ // go함수 하나마다 3번 호출
go(N - 1);
}
return;
}
int main(){
cin >> N;
go(N);
return 0;
}
/*
n = 3 -> cnt = 40 (go함수의 호출 횟수)
*/- 재귀함수의 시간복잡도 = (메인 로직의 시간복잡도) * (함수의 호출 횟수)
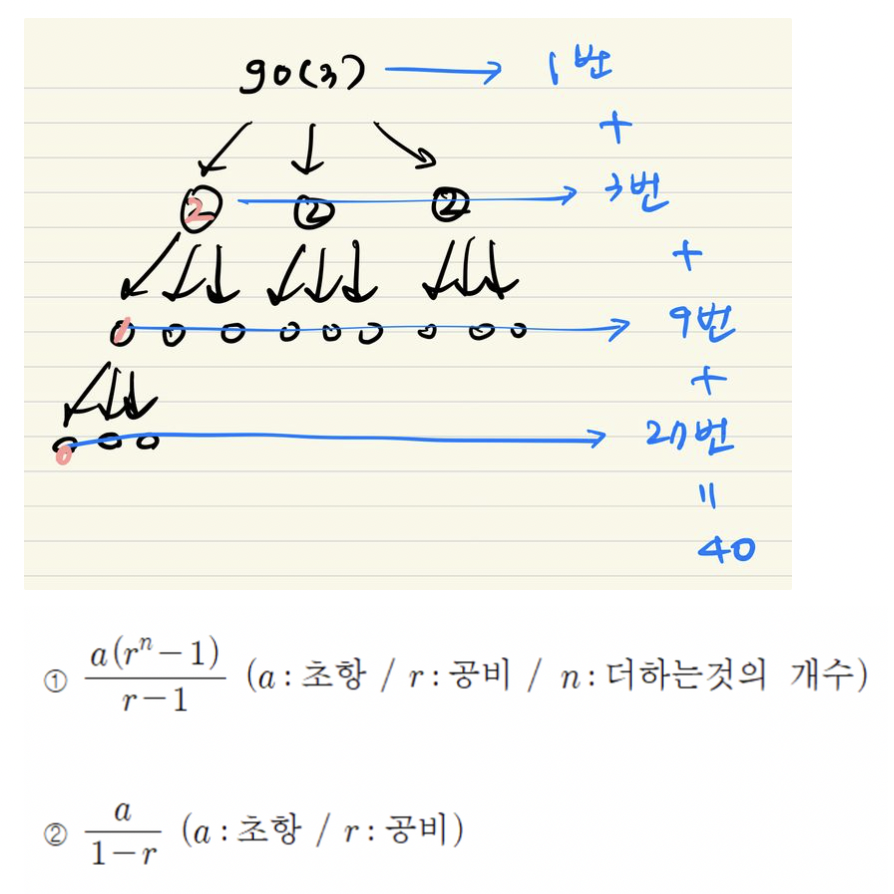
(3^n-1)/2→O(3^n)*O(1)=O(3^n)- 꿀팁) 재귀함수 하나 당 10번 호출하면 10^n (메인 로직 말고 호출되는 횟수)
시간복잡도의 존재 이유
- 코테에서 알고리즘을 유추 할 수 있다.
- 면접에 나온다.
- 코드 개선의 기준이 된다.
- 이중 for문(
O(n^)) 보다 for문(O(n))이 낫다. - for문 보다 lower_bound(이중탐색 알고리즘)가 낫다. (
O(log n)) - 코드 개선의 기준은 많다.
- 프론트엔트 PageSpeedInsights
- 이중 for문(
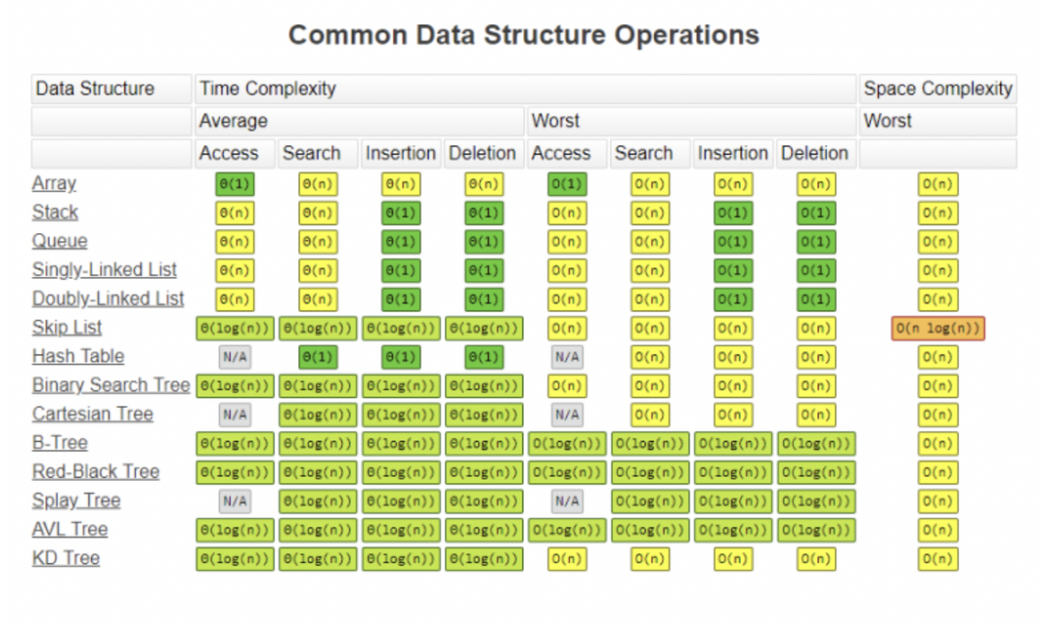
자료구조 별 시간복잡도
- 어떠한 요소들의 모음에서 k번째 요소를 계속해서 ‘탐색’해야 하는 로직이라면, O(k)의 시간복잡도인 연결리스트 보다 O(1)인 배열이 낫다.
- 문제를 풀때 시간초과가 나는 것은, 내가 선택한 자료구조의 평균 시간복잡도가 O(1)이라 해도 문제 내부의 테스트 케이스에서 최악의 경우인 O(n)인 상황이 발생 하기 때문이다. 그러므로 최악의 시간복잡도를 고려해야 한다.
- 대표적 자료구조들의 최악의 시간복잡도
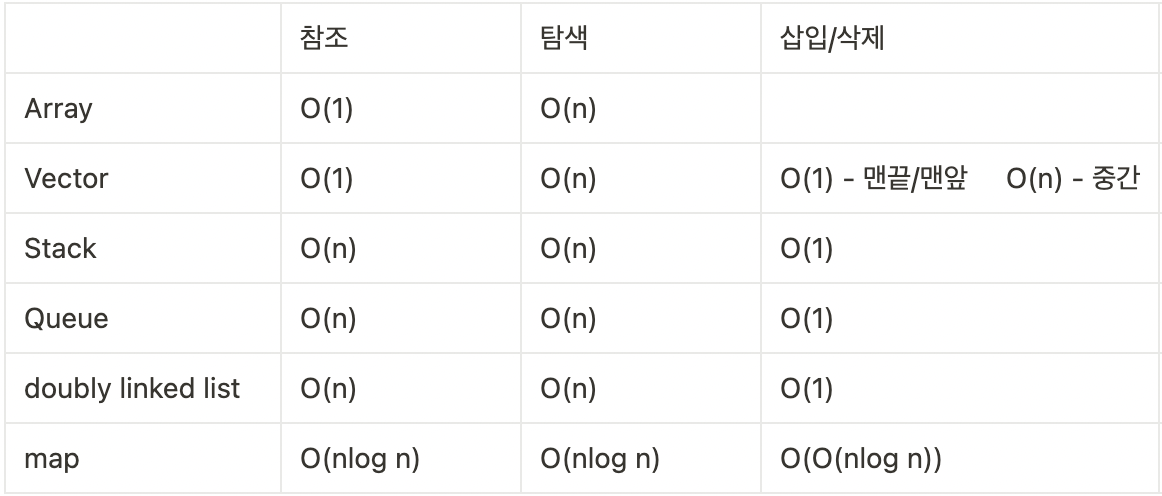
- 이 외에 자료구조들의 시간복잡도