HashTable

• 실무에서도 활용도가 높은 자료구조
• LinkedList, Array, Tree 까지 질문 가능
• 시간복잡도에 대해 묻기 좋다.

Direct-address Table (직접 주소화 테이블)

• key 값을 인덱스로 테이블/배열 형성

• 문제점1 : 불필요한 공간 낭비
  • 2022390 처럼 큰 수부터 시작하는 경우
• 문제점2 : key가 다양한 자료형을 담을 수 없다.
  • 인덱스로는 숫자만 가능하다.
• 직접 주소화 방식의 문제점을 보완하기 위해 → HashTable

HashTable

• (key, value) 데이터 쌍 저장하므로 직접 주소화 방식이 잘 맞지 않는다.
  • 키는 무조건 존재해야 하며, 중복될 수 없다.
  • (key, value) 데이터를 저장하는, hash table을 구성하는 각각의 공간을 slot 또는 bucket 이라고 한다.
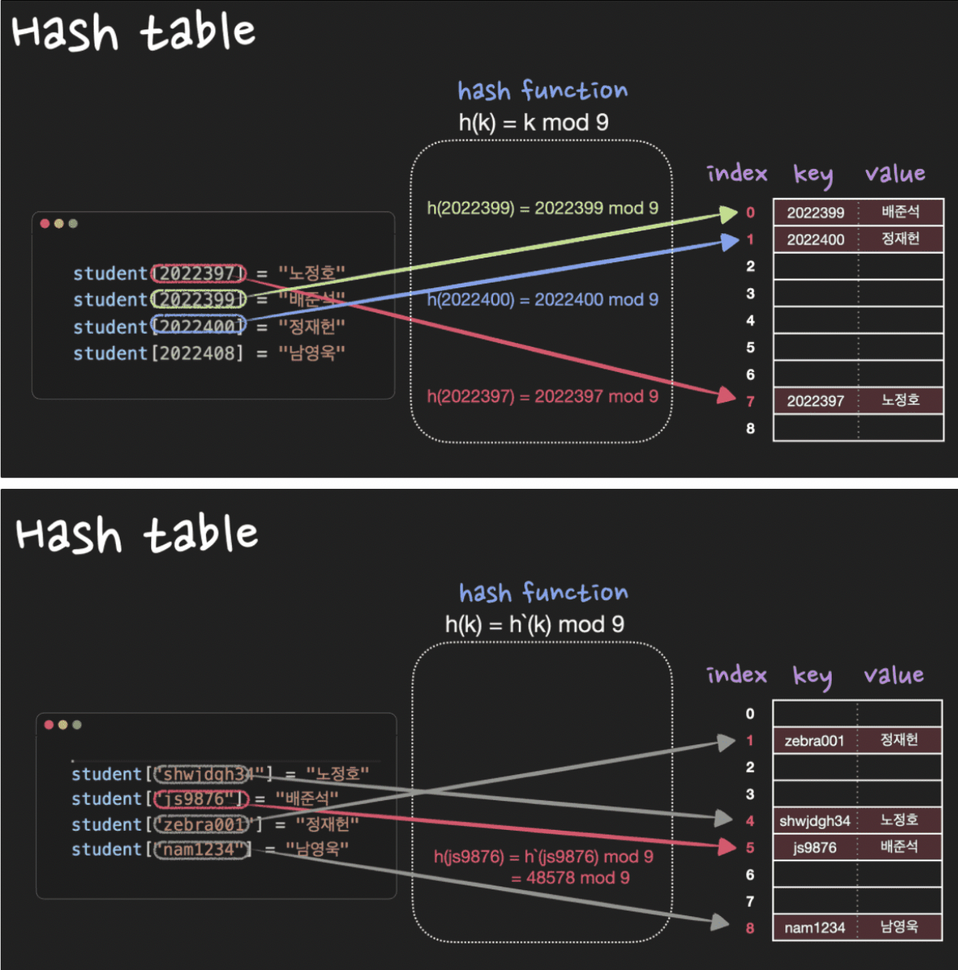
• hash function h에 key값을 입력으로 넣어 얻은 해시값 h(k)를 위치로 지정하여 key-value 데이터 쌍을 저장한다.
  • “키 k값을 갖는 원소가 위치 h(k)에 hash된다.” 또는 “h(k)는 키 k의 해시값이다.” 라고 표현한다.
  • (key, value)
  • h(k) = 저장위치(인덱스) = 해시값(해시함수의 반환값)
  • vlaue = 저장되는 데이터

시간복잡도와 공간 효율

• 시간 복잡도는 저장, 삭제, 검색 모두 기본적으로 O(1) 이지만, collision으로 인하여 최악의 경우 O(n)이 될 수 있다.
• 데이터가 저장되기 전 미리 저장공간(slot, bucket)을 확보해야 하므로 공간효율성은 떨어진다. 저장공간이 부족하거나 채워지지 않은 부분이 많은 경우가 생길 수 있다.

Collision

• 서로 다른 키의 해시값이 똑같은 경우를 말한다.
  • 중복되는 키는 없지만, 해시값은 중복될 수 있다.
• collision이 최대한 적게 발생하도록 hash function을 잘 설계해야 한다.
• seperate chaining 또는 open addressing 등의 방법을 사용하여 해결한다.

hash function

• 좋은 hash function의 핵심 조건은, 해시값이 고르게 분포되게 하는 것이다.
• 만능의 해시함수는 없으며 상황마다 달라지지만, 대략적인 기준으로 연산속도가 빨라야 하고, 해시값이 최대한 겹치지 않아야 한다.

open addressing

• collision이 발생하면 미리 정한 규칙에 따라 hash table의 비어있는 slot을 찾는다.
  • 추가적인 메모리를 사용하지 않으므로 linked list 또는 tree 자료구조를 통해 추가로 메모리를 할당하는 seperate chaining 방식 보다 메모리를 적게 활용한다.
  • 규칙은 방법에 따라 크게 Linear Probing, Quadratic Probing, Double Hashing 으로 나뉜다
• Linear Probing(선형 조사법), Quadratic Probing(이차 조사법)
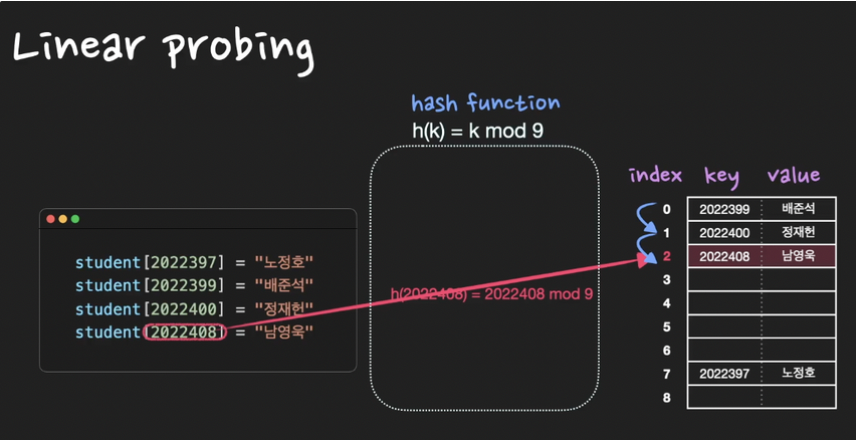
  • 충돌이 발생한 해시값으로 부터 일정한 값만큼(+1, +2, +3, …)(한칸씩) 건너띄어 비어있는 slot에 데이터 저장
  • 이차 조사법은 (+1^, + 2^, +3^, …)(제곱수로 건너띄기)
  • 충돌이 여러번 발생하면, 여러번 건너띄어 빈 slot을 찾는다
  • 충돌 횟수가 많아지면 특정 영역에 데이터가 집중적으로 몰리는 클러스터링(clustering) 현상이 발생하므로 평균 탐색 시간이 증가하는 단점이 있다.

• Double Hashing(이중해시, 중복해시)
  • 선형/이차 조사법은 탐사 이동폭이 같으므로 클러스터링 문제 발생
  • 클러스터링 문제가 발생하지 않도록 2개의 해시함수를 사용하는 방식
    • 하나는 최초의 해시값에, 다른 하나는 해시 충돌 발생시 탐사 이동폭을 얻는데에 사용

seperate chaining

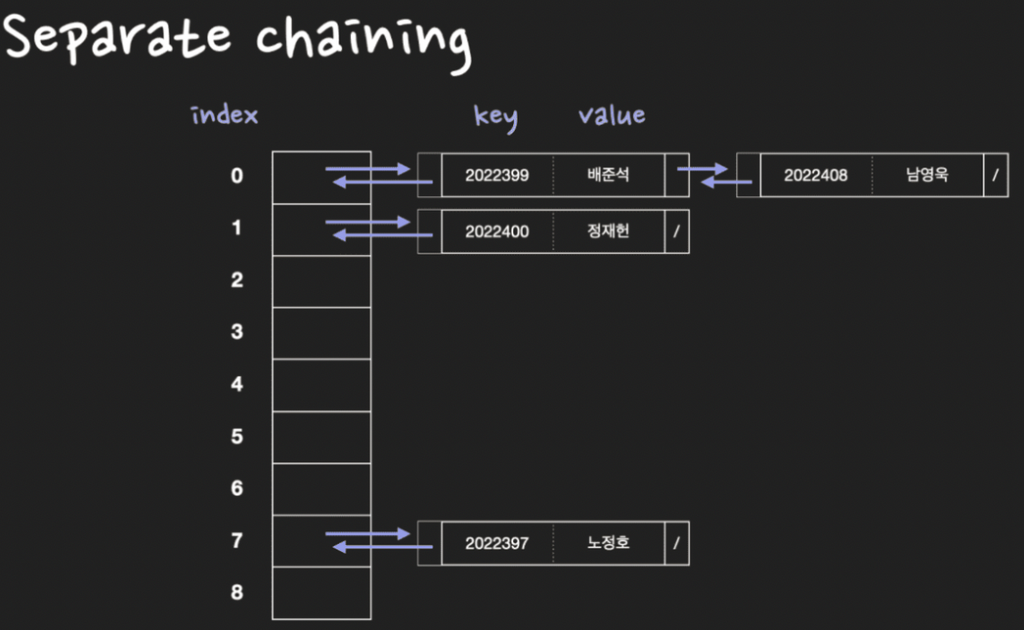
• collision이 발생하면 linked list 또는 tree에 노드(slot)를 추가하여 데이터를 저장한다.
• 삽입, 검색, 삭제의 시간복잡도는 O(1) 이지만, worst case의 경우에 O(n)이 될 수 있다.
  • 삽입 : 서로 다른 key가 같은 해시값을 갖게 되면, linked list에 node를 추가하여 (key, value) 데이터 쌍 저장. 시간복잡도 O(1)
  • 검색 : 기본적으로 O(1) 이지만 최악의 경우 O(n)
  • 삭제 : 삭제 하기 위해 검색 먼저 하므로 검색의 시간복잡도와 같다.
• worst case : n개의 모든 key가 동일한 해시값을 가지면, n개의 linked list 생성되므로 검색의 시간복잡도 O(n)
  • linked list 대신 Binary Search Tree(BST)에 저장하여 시간복잡도를 O(n) → O(logn) 으로 낮출 수 있다.