학습 목표: 최적의 파라미터를 찾기 위한 알고리즘인 GD를 알아보자.

1. Gradient Descent (GD)

이전에 배웠던 손실함수를 다시 생각해면

최적의 $\theta$를 찾는 것은 Loss가 최소화 되는 지점을 찾는 것이다.
따라서 손실함수의 gradient가 0이 되는 지점이 loss가 극소값을 갖는다고 할 수 있다. (local or Global)

그렇다면 0이 아닌 지점에서 손실함수의 gradient가 0이되는 지점까지 이동하는 과정은 다음과 같다.

1. initialize at random point $\theta_0$
2. at i-th step,
   2.1 compute gradient $\nabla \mathcal{L}(\theta_i)=\frac{1}{n}\sum_{i=1}^n\nabla l(g_\theta(x_i),y_i)$
   2.2 Update parameter: $\theta_{i+1}=\theta_i-\alpha\nabla\mathcal{L}(\theta_i)$$\quad\alpha$: Learning rate
3. untill convergence

$\nabla \mathcal{L}(\theta_i)$는 손실 함수가 증가하는 파라미터의 방향(기울기)을 알려준다. 우리는 이 경사를 따라 내려가야 최소점에 도달할 수 있다.
손실 함수가 작아지는 방향은 $-\nabla \mathcal{L}(\theta_i)$이고 기존 파라미터에 더하여 업데이트한다.
이때, learning rate는 업데이트하는 크기를 조절해준다. 만약 $\alpha$가 큰 값을 가진다면 한번에 큰 폭으로 파라미터를 이동하는 것이고, 작은 값이면 소극적으로 파라미터를 움직이는 것이다.
learning step이라고도 불린다.

간단한 예시로 $f(x)=(x-3)^2$인 함수의 gradient를 통해 최소점을 찾아보고 learning rate가 왜 step으로 불리는지 확인해보자.

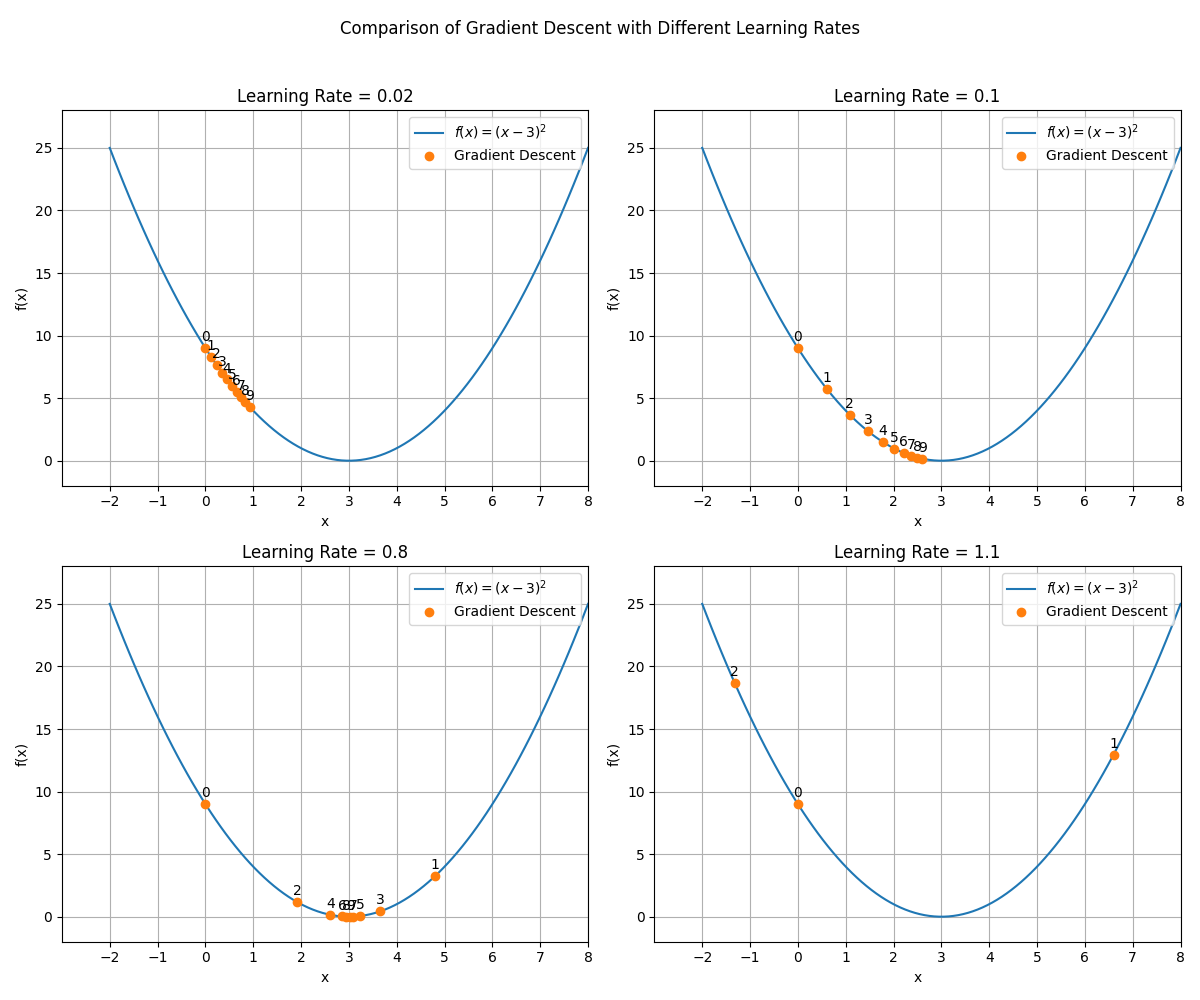
4가지 그래프 모두 $x=0$인 지점에서 시작해 함수 f의 gradient를 계산하고 x의 위치를 업데이트한 모습이다. 앞에서 설명한 것과 같이 기울기와 반대 방향으로 이동하는 것을 확인할 수 있다.
각 learning rate의 값은 [0.02, 0.1, 0.8, 1.1]으로 x가 이동하는 step이 learning rate의 값에 비례한다. 또한 아래 두 그래프는 step이 큰 편이라 최소점을 지나게 되어 지그재그로 업데이트 된 것을 알 수 있다.

왼쪽 그래프는 점점 최소값으로 수렴하게 되고 오른쪽 그래프는 step이 너무 커서 발산하므로 최소점으로부터 멀어진다.

따라서 최적값을 얻기 위해 적절한 learning rate를 선택하는 것이 중요하다.

추가로 $f(x,y)=(1-x)^2+5(y-x^2)^2$를 같은 방법으로 살펴보면

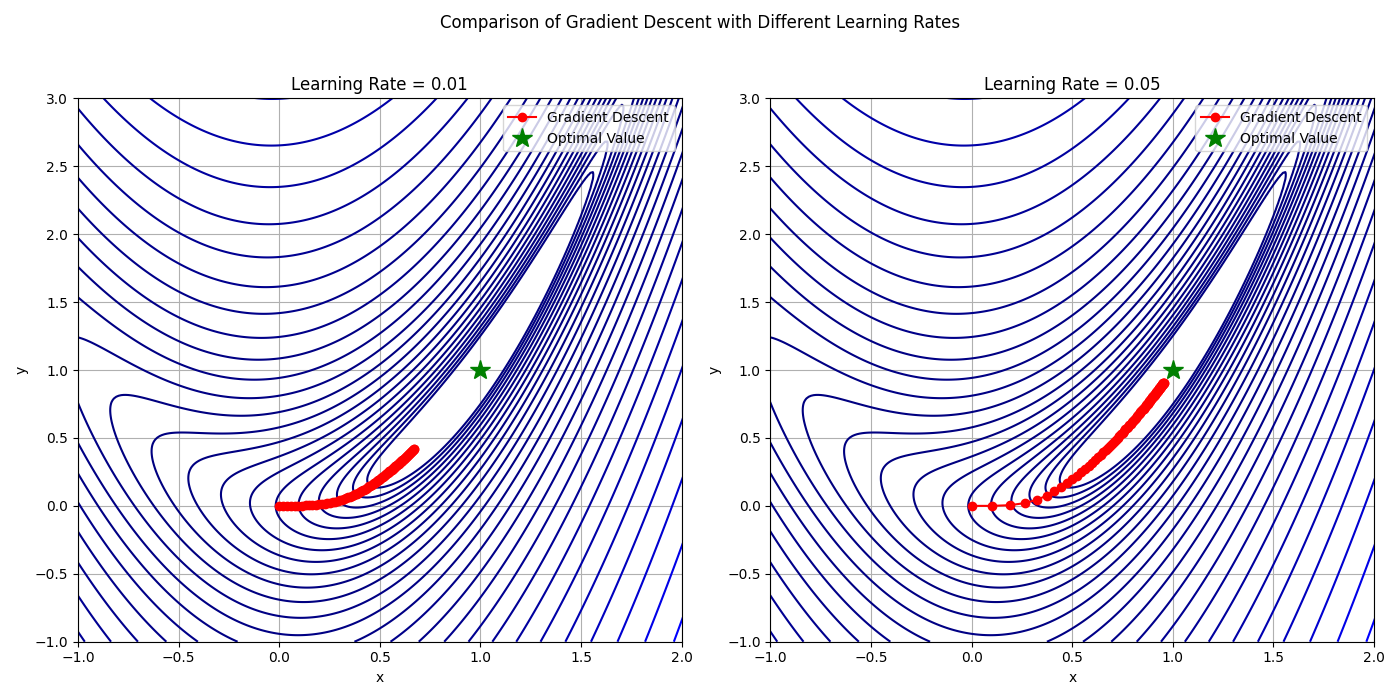
Optimal point는 (1,1)이고 50번 반복하여 (x,y)를 GD로 업데이트 하였다. learning rate를 조절함에 따라 동일한 계산 횟수로 더 빠르게 최적의 값을 찾을 수 있다.

2. Stochastic Gradient Descent (SGD)

GD는 손실함수의 gradient를 계산하고 업데이트 할 때, 모든 데이터에 대해서 계산하고 그 평균값을 사용한다. 따라서 데이터의 크기가 클수록 한 번 업데이트하는데 계산량이 많아진다.
이러한 단점을 보안하기 위해 하나의 데이터만 계산하여 업데이트하는 방식을 SGD라고 한다.

1. initialize at random point $\theta_0$
2. at i-th step,
   2.1 compute gradient $\nabla \mathcal{L}(\theta_i;x_i,y_i)=\nabla l(g_\theta(x_i),y_i)$
   2.2 Update parameter: $\theta_{i+1}=\theta_i-\alpha\nabla\mathcal{L}(\theta_i;x_i,y_i)$
3. untill convergence

모든 데이터에 대해서 gradient를 구한 것이 아니기 때문에 노이즈가 있다. 하지만 계산상 이점이 크게 반영된다.

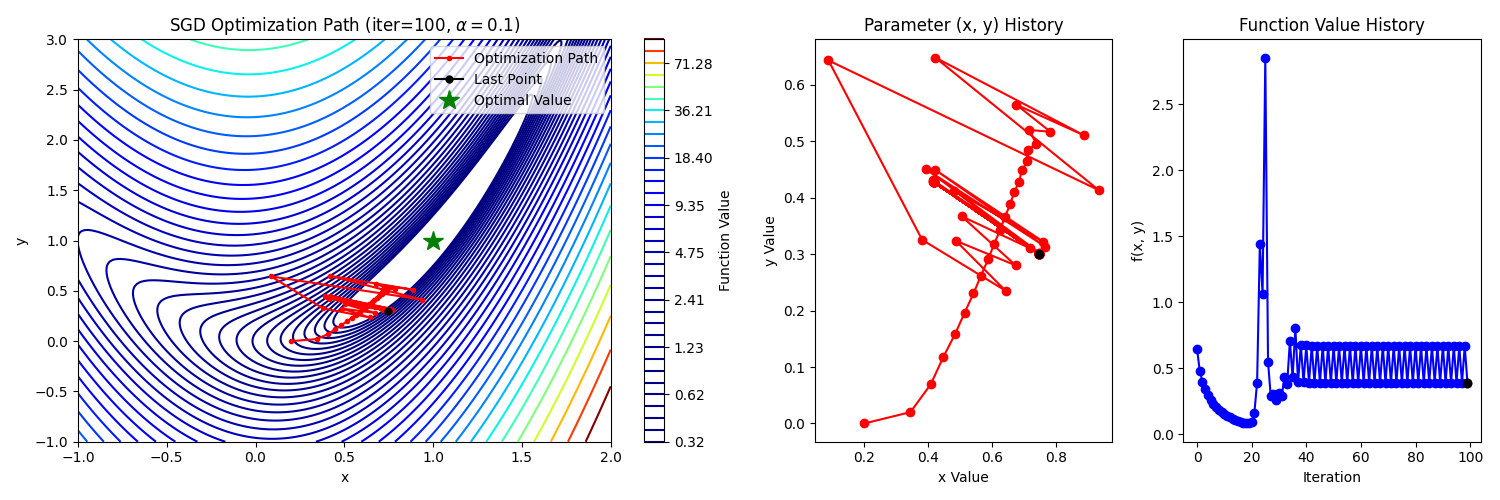
3. Mini-batch Gradient Descent

GD와 SGD의 절충안으로 전체 데이터 셋(N)중 batch로(b) 나누어 선택하여 업데이트하는 방법이다. 이점은 GD보다 계산량은 작고 SGD에서 노이즈 영향을 줄여 안정적으로 수렴에 도달한다는 것이다.

1. initialize at random point $\theta_0$
2. at i-th step,
   2.1 compute gradient $\nabla \mathcal{L}(\theta_i;B)=\frac{1}{b}\sum_{i\in B}\nabla l(g_\theta(x_i),y_i)$
   2.2 Update parameter: $\theta_{i+1}=\theta_i-\alpha\nabla\mathcal{L}(\theta_i;B)$
3. untill convergence

4. Momentum SGD

SGD의 변형으로 관성을 가지는 방식이다. SGD는 매 순간의 gradient 값을 통해 업데이트하여 개별 데이터에 따라 방향이 크게 바뀔 수 있다. 여기에 이전 스텝 동안의 관성을 부여한다면 전체 데이터가 보편적으로 가지고 있는 방향으로 유도하여 수렴 속도를 증가시킨다. 또한 gradient가 0이 되는 경우에도 관성에 의해 바로 멈추지 않고 이동하므로 local minimum에 빠지는 현상을 줄이는 이점을 갖는다.

• weighted average of gradients

  $v_t=\beta v_{t-1}+(1-\beta)\mathcal{L}(\theta_{t-1})\quad (0\leq\beta<1)$

  만약 $\beta=0$이면 GD 또는 SGD와 같고 $\beta$가 커질수록 관성(과거값)에 의존하게 된다.

• update Parameters

  $\theta_{t}=\theta_{t-1}-\alpha v_t$

  이 방식은 관성에 의해 현재 gradient보다 밀리는 현상이 나타난다. 이를 해석해보면

  $\begin{aligned} v_t=\beta v_{t-1}+&(1-\beta)\mathcal{L}(\theta_{t-1})\\ v_{t-1}=\beta v_{t-2}+&(1-\beta)\mathcal{L}(\theta_{t-2})\\ v_{t-2}=\beta v_{t-3}+&(1-\beta)\mathcal{L}(\theta_{t-3})\\ &\vdots\\ v_t=\beta^0(1-\beta)\mathcal{L}(\theta_{t-1})+\beta^1(1-\beta)\mathcal{L}(\theta_{t-2})+&\beta^2(1-\beta)\mathcal{L}(\theta_{t-3})+\dots++\beta^{t-1}(1-\beta)\mathcal{L}(\theta_{0})+\beta^tv_0,\quad v_0=0\\ \;\\ v_t=(1-\beta)\sum_{i=0}^{t-1}&\beta^i\nabla\mathcal{L}(\theta_{t-i-1}) \end{aligned}$

  이전에 계산했던 값이 계속 더해지지만 그 크기가 $\beta$의 거듭제곱으로 곱해져 지수적으로 감소한다.
  

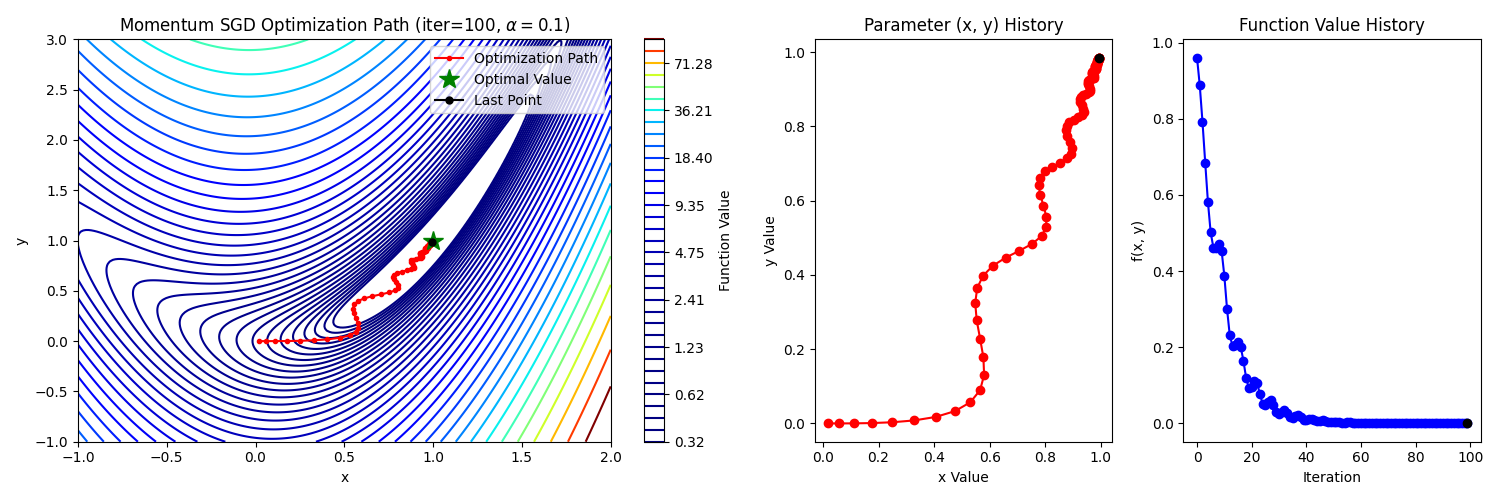
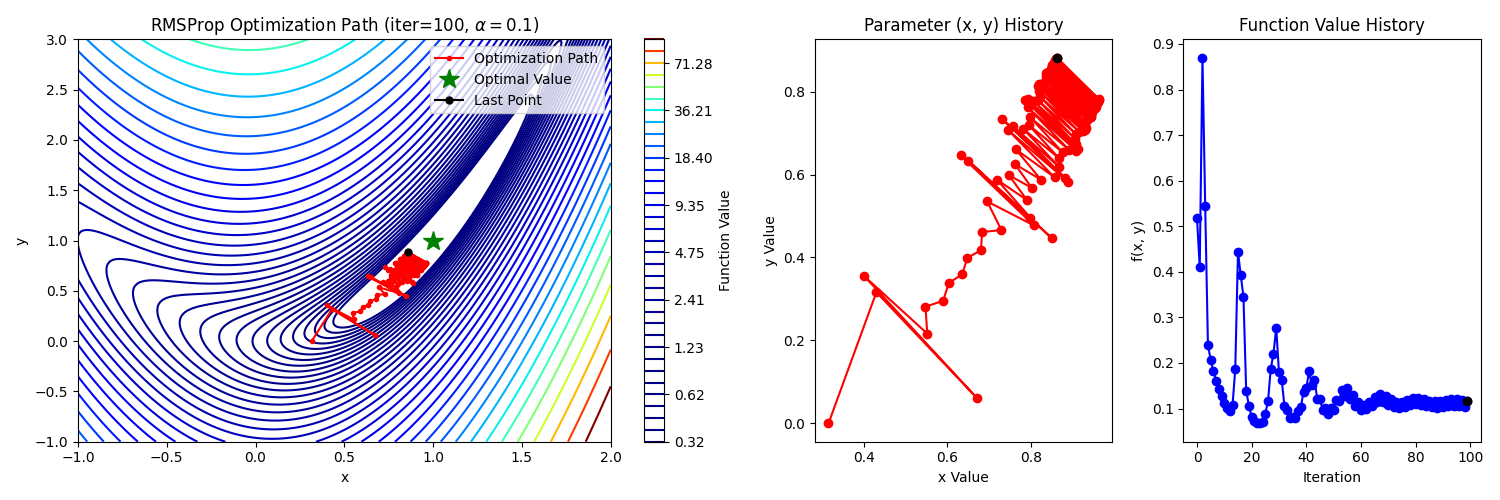
5. RMSProp

Root Mean Square Propagation의 약자로 gradient 제곱의 지수 이동 평균을 계산하여 적응형 학습률(step size)을 업데이트 하는 것이 특징이다. 자주 업데이트되는 파라미터는 학습률을 줄이고, 드물게 업데이트되는 파라미터는 상대적으로 큰 학습률로 조정한다.

업데이트 방식은 다음과 같다.

$g$는 gradient를 의미하고 E는 평균, $\epsilon$은 수치적 안정성을 위해 사용되는 작은 값 ( 분모가 0이 되는 것 & g가 작을때 과한 업데이트 방지)

과정을 설명하자면
식 (2)에서 $\alpha$가 고정되어 있지만 분모에 들어가는 값에 따라 업데이트 되는 step size가 달라지는 것으로 이해할 수 있다. $E[g^2]$(gradient의 RMS)가 작다면 큰 보폭으로, 크다면 작은 보폭으로 업데이트한다.
식(1)에서 RMS값은 과거 값을 포함하여 gradient의 크기가 반영된다.

따라서 기울기가 크다면 변동성이 크다는 뜻이고 조심해서 작은 보폭으로 이동한다.
반대로 기울기가 작다면 변동성이 작으므로 보폭을 키우는 편이 합리적이다.

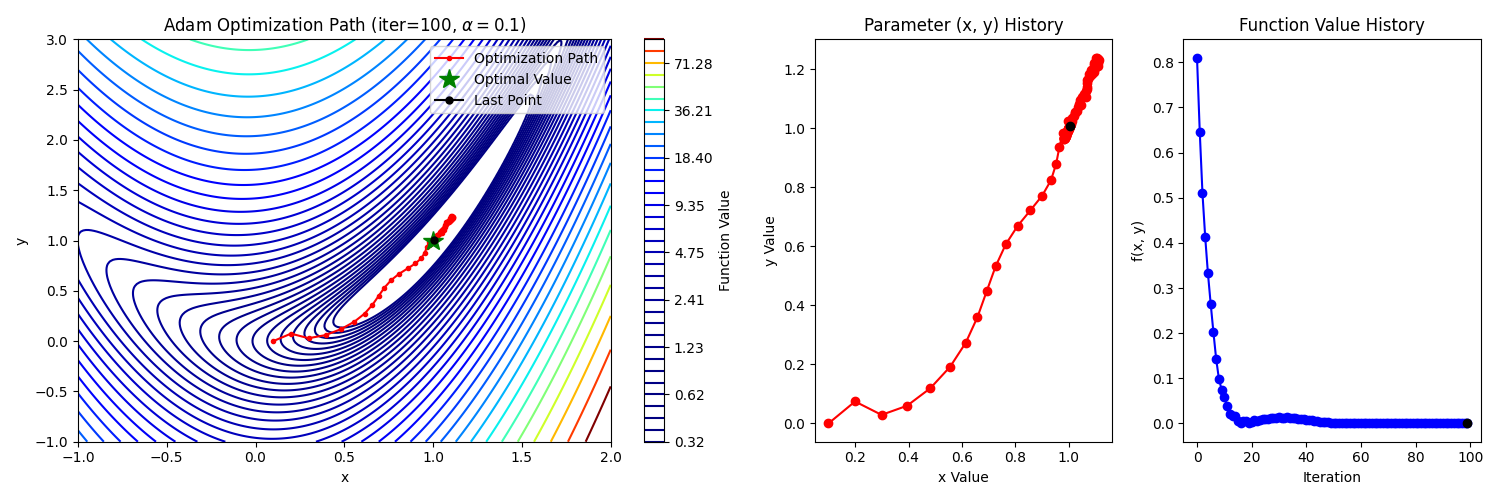
6. Adam

Momentum + RMSProp으로 구성한 알고리즘으로 대부분의 최적화 문제에서 좋은 성능을 보인다고 알려져 있다. momentum은 gradient의 1차 모멘트(평균), RMSProp은 2차 모멘트(분산)라고 생각할 수 있다.

식(1)은 momentum, 식(2)는 RMSProp과 동일한 과정이다.
식(3)에 사용된 편향 보정은 초기 스텝에서 더 정확한 모멘트를 제공한다.

추천되는 parameter의 크기(defualt)는 $\beta_1=0.9,\;\beta_2=0.999,\epsilon=10^{-8}$,
$\alpha$는 문제에 따라 적절한 값으로 찾아야한다.

Learning rate scheduling

• 1. Scheduling
     특정 Epoch마다 learning rate를 감소

     $0\leq d<1$
     Update learning rate every s steps:
     if epoch % s == 0:
     $\quad\quad\alpha$ = $\alpha$ x d
     end if

• 2. Exponential Scheduling
     매 순간 exponential하게 learning rate 감소

     Update learning rate:

     $\begin{aligned} &\alpha = \alpha_0\times e^{-\gamma t}\\ &t:=t+1 \end{aligned}$

• 3. Adaptiove Scheduling (Annealing)
     validation loss를 계산하여 이전보다 발전이 없으면 learning rate를 감소

     Compute validation loss $\mathcal{L}_{val}$

     $if\; \mathcal{L}_{val}<\mathcal{L}_{best}:\\ \quad \mathcal{L}_{best}:=\mathcal{L}_{val}\\ Reset\; patience\; counter\; k=0\\ else\\ \quad Increment\; patience\; counter\; k:=k+1\\ end if\\ if\; patience\; counter\; k\geq p\quad then\\ \quad Update\; learning\; rate:\\ \quad\quad\quad\quad \alpha:=\alpha\times d\\ \quad Reset\; patience\; counter\; k=0\\ end\; if$

정리

• Gradient Descent는 임의의 점에서 가장 빠르게 함수값이 줄어드는 방향으로 이동하여 최적의 값을 찾는 알고리즘이다.

• 업데이트에 사용하는 데이터의 크기에 따라 GD, SGD, Mini-batch GD로 구분한다.
  관성을 주어 gradient의 방향을 조절하는 방법과 gradient의 크기를 이용하여 step size를 조절하는 방법을 배웠다. 특히, 두 가지를 합성한 Adam Optimizer는 보편적으로 효율이 좋다.

• 문제에 따라 적절한 Learning Rate를 찾는 것이 중요하고 고정된 값이 아니라 다양한 scheduling을 통해 변화시킬 수 있다.

참고 영상

• Youtube - Andrew Ng(C2W2L05)