학습 목표: 지도학습 중 분류에 대하여 공부해보자.

• 목차

1. Perceptron & LP (perfect separation case)
2. SVM (perfect separation case)
3. Soft-margin SVM (Non-perfect separation case)

Binary Classification

-1과 1로 나눌 수 있는 label에 대한 분류 방법

Linear Classifiers

• dataset
  $x^{(i)}=(x_1,x_2,x_3,\dots,x_N), y^{(i)}\in\{-1,1\}$
• set function class:
  $G=\{g_{a,b}(x)=sign(a^\top x+b)\}$
• set loss function: 0-1 Loss
  $l(g_{a,b}(x^{(i)}),y^{(i)})=1(g_{a,b}(x^{(i)})\ne y^{(i)})$
• Assumption: Data is linearly separable:
  There exists a perfect classifier with Loss=0

주어진 데이터를 구분할 때, 사용되는 모델이 선형이며 완벽하게 구분 가능하다고 가정(Loss=0)

1. Perceptron Algorithm

initialize random values: a,b
Set learning rate: $\eta$

$Repeat\\ \quad for\; each\; training\; sample\; (x,y)\; do\\ \quad\quad Compute\; the\; weighted\; sum:\; z_i=a\cdot x_i+b\\ \quad\quad Predict\; the\; label:\; \hat y_i = sign(z_i)\\ \quad\quad if\; \hat y_i\ne y_i\; then\\ \quad\quad\quad Update weights:\; a:=a+\eta(y_i-\hat y_i)x_i\\ \quad\quad\quad Update bias:\; b:=b+\eta(y_i-\hat y_i)\\ \quad\quad end\; if\\ \quad end\; for\\ until\; convergence$

장점:

• gradient 계산 등이 없어 간단하게 업데이트 가능
• 정답이 있다면 항상 수렴

단점:

• 정답이 없는 경우 멈추지 않고 계속 동작
• 정답이 없어서 도는지, 수렴하는 과정인지 구분 불가

2. Linear Programming

모든 데이터 x에 대해서 $g_{a,b}(x)$의 부호가 정답과 같은 것을 찾는 문제가 되며 이를 feasible problem이라 부른다. 제한 조건은 정답과 예측값의 부호가 같아서 곱하면 1이 되는 경우를 의미한다. 만약 잘못 분류하였다면 $y_i(a\cdot x_i+b)$가 음수를 나타낸다.

LP는 해결 알고리즘이 알려져 있어 쉽게 풀 수 있다. 또한 정답이 없는 경우(infeasible)를 알려준다.
하지만 feasible한 솔루션 중 어느 것이 더 좋은 성능인지 알 수 없다.

예시)

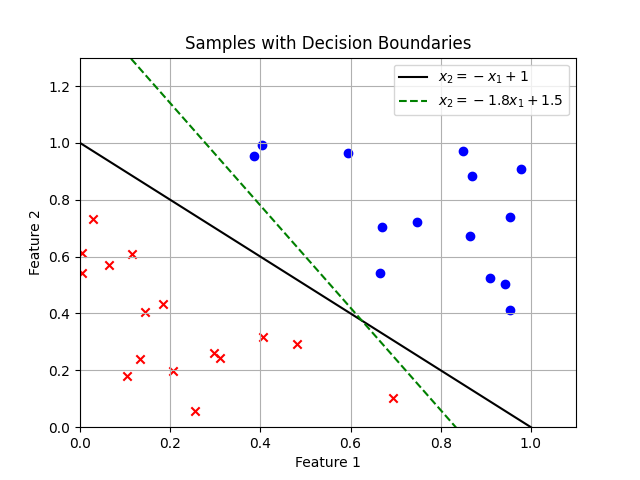
우리가 원하는 것은 가장 성능이 좋은 최적의 파라미터를 찾는 것이고 데이터가 경계선에서 멀리 떨어져 있을수록 더 좋은 분류를 한 것이다.

Margin

분류기가 주어졌을 때, 경계면과 가장 가까운 데이터를 선택하고 그 거리를 마진이라고 부른다.
따라서 마진을 최대화 하는 것이 최적의 경계를 찾는 것이다.

마진은 다음과 같이 계산한다.

마진의 값이 큰 모델이 더 견고하며 최적의 성능을 만든다.

Support Vector Machine (SVM)

마진을 최대화 한다는 것은 마진의 분자값을 1로 고정하고 분모값을 최소화하는 것과 같다.
Convex Optimization Problem이며 QCQP에 해당하는 케이스이다.
이와 같이 완벽히 구분 가능한 문제의 경우, 마진을 통해 분류기의 성능을 비교할 수 있다.
하지만 완벽히 구분 가능한 문제가 아니라면 어떻게 해결하는가?

Soft-margin SVM

Convex optimization에서 slack variable을 도입하는 경우(penalty)에 해당한다.

SVM과 차이점을 보면 목적함수와 제약 조건에 $\xi$ 항이 추가되었다. SVM에서는 엄격하게 제약조건을 모두 만족해야 한다면 Soft-margin는 $\xi$항으로 데이터에 대해서 제약 조건을 만족하도록 추가 cost를 제공해준다. 추가로 제공 받은 cost만큼 목적함수에 더해주어 우리의 목표는 최대한 큰 마진을 가지며 제약 조건을 만족시키기 위한 비용을 최소화하는 것이다.
목적함수의 C값은 마진과 penalty에 대해서 어떤 것에 더 초점을 맞출 것인지 정하는 변수이다.

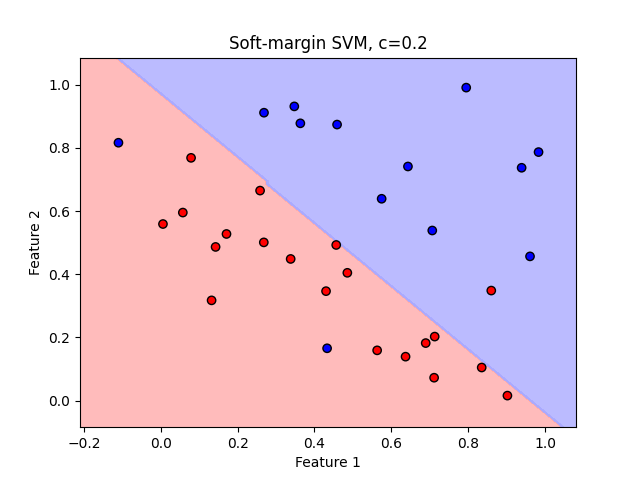
만약 C가 작으면 마진이 큰 파라미터를 선택한다.
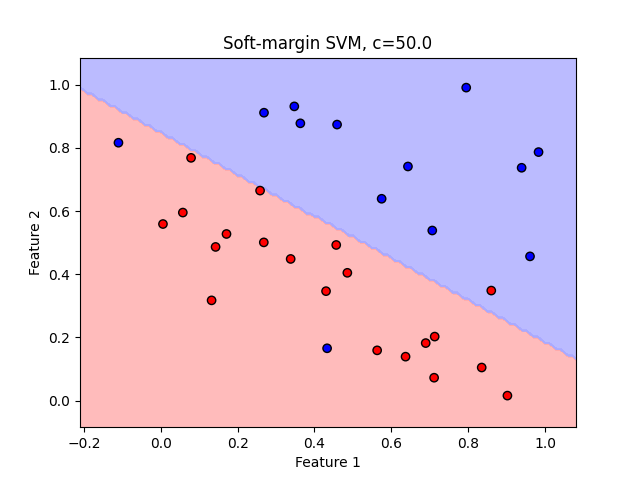
반대로 C가 크다면 penalty를 최소화하도록 선택한다.

• Small C - focus on regular
  
• Large C - penalize outlier
  

SVM Loss function (Hinge Loss)

• $y=max(0,1-x)$

  $\mathcal{L}(y_i,f(x_i))=max(0,1-y_i(a^\top x_i+b))$

• objective function:

  $\frac{1}{2}||a||^2+C\sum_{i=1}^n\mathcal{L}(y_i,f(x_i))$

정리

이진 분류에 대해서 알아보았습니다.

데이터를 완벽하게 분리하는 경우

• Perceptron Algorithm: 0-1 loss is not differentiable
• SVM
  • 0-1 loss
  • Not differentiable
  • Only considers the points near boundary

데이터를 완벽하게 분리하는 않는 경우 ( Slack variable - Penalty )

• Soft-margin SVM
  • Only considers points near boundary and violation points
  • Requires convex optimization