학습 목표: 분류에서 Logistic Regression으로 확장하는 과정을 알아보자

목차
1. Soft Guess
2. Logistic Regression
3. Multi-class classification
4. Confusion Matrix

1. Soft Guess

SVM에서 마진을 사용하면 대부분의 데이터는 의사 결정(파라미터 조정)에 참여하지 못하고 경계면에 가장 가까운 데이터만 사용한다는 단점이 있다. 만약 새로운 데이터가 들어왔을때, 경계와 멀리 떨어진 경우가 상대적으로 경계 근처보다 확신(신뢰)을 가지고 예측할 수 있다.

이진 분류 알고리즘에서 0-1 Loss를 사용한 것처럼 여러 클래스 중 하나의 클래스만 선택하는 경우를 Hard guess라고 말한다. 경계면 근처에 있는 데이터의 경우 Hard guess의 신뢰성을 표현하기 어렵다. 따라서 하나의 클래스만 선택하는 것이 아니라 각각의 클래스일 확률을 결과로 나타낸다면 결정의 신뢰성을 표현할 수 있게 된다. 이 경우를 Soft Guess라 한다.

• Hard Guess

  $g_\theta(x^(i))=1\; or\;-1$

• Soft guess

  $g_\theta(x^{(i)})=\begin{bmatrix} Pr(y^{(i)}=-1)\\ Pr(y^{(i)}=1)\end{bmatrix}$

2. Logistic Regression

2.1 Logistic function

• Logistic function
  $\sigma(x)=\frac{1}{1+e^{-x}}$

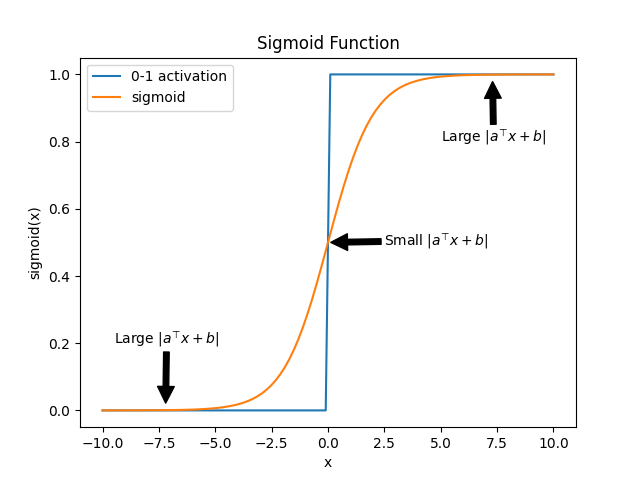
Hard guess와 Soft guess의 차이를 확인할 수 있다. 경계면 근처($|a^\top x+b|=0$)에서 0-1의 경우 급격하게 변하지만 sigmoid는 0과 1사이 값이 부드럽게 나타나며 확률로 작동할 수 있다.

• models probability

  $g_{a,b}(x)=\begin{bmatrix} 1-\sigma(a^\top x+b)\\ \sigma(a^\top x+b) \end{bmatrix}$

• Model class

  $\Large \mathcal{G}=\left\{g_{a,b}(x)=\begin{bmatrix} \frac{e^{-(a^\top x+b)}}{1+e^{-(a^\top x+b)}}\\ \frac{1}{1+e^{-(a^\top x+b)}}\end{bmatrix}\right\}$

2.2 Cross Entropy Loss (CEL)

만약 비가 내릴 확률을 출력하는 분류기가 있고 Logistic하다고 가정하자.

비가 올 확률이 70%, 오지 않을 확률이 30%라고 예측했다면 $\hat y(1)=0.7$, $\hat y(-1)=0.3$으로 표현할 수 있다.

모델이 예측한 확률값과 실제 정답 간의 차이를 측정하기 위해 크로스 엔트로피 손실(Cross Entropy Loss)을 사용한다. 크로스 엔트로피 손실은 실제 레이블의 확률 분포와 모델이 예측한 확률 분포 간의 Kullback-Leibler (KL) divergence (또는 상대 엔트로피)에서 유도되었다. KL divergence는 두 확률 분포 간의 차이를 측정하는 지표이다.

• KL divergence
  $D(p\mid\mid q)=\sum_xp(x)log(\frac{p(x)}{q(x)})$
  p(x): 정답 분포, q(x): 예측 분포

비가 왔을 때($Y=1$), 비가 올 확률(0.3)과 오지 않을 확률(0.7)을 예측했다면 분포의 차이에 해당하는 KL divergence는 다음과 같이 계산할 수 있다.

• Cross Entropy
  KL을 풀어서 써보면

  $\begin{aligned} D_{KL}(p\mid\mid q)&=\sum_xp(x)log(\frac{p(x)}{q(x)})=\sum_xp(x)log(p(x))-\sum_xp(x)log(q(x))\\ &=-H(p)+H(p,q)\end{aligned}$

  $H(p)$는 P분포의 정보 엔트로피를 의미하며 $H(p,q)$가 교차 엔트로피이다.
  다시 적어보면

  $H(p,q)=H(p)+D_{KL}=-\sum_xp(x)log(q(x))$

  로 P분포에 대해 Q분포가 얼마나 차이가 나는지 확인할 수 있다. 모델이 정확한 예측으로 정답과 같다면 $D_{KL}=0$이 되며 최소값 $H(p)$가 된다. 따라서 예측값 Q가 정답 P에 가까울수록 교차 엔트로피는 낮아진다.
  또한 손실 함수로 사용하기에 미분이 용이한 장점이 있다.
  $D_{KL}$에서 P에 대한 엔트로피 $H(p)$의 경우 최적화(파라미터)에서 상수값에 해당한다.

• Cross Entropy Loss function
  이진 분류의 손실함수를 살펴보면
  $\large Pr(Y=1)=g\theta(x)=\frac{1}{1+e^{-\theta^\top x}}$

  $\large Pr(Y=-1)=1-g\theta(x)$
  

y=1이면 첫째 항만 살아남고 y=-1이면 둘째 항만 살아남는다.
더 단순화 하기 위해 $g_\theta$에 logistic 함수를 대입해서 생각하면
$\large -log(g\theta(x))=log(1+e^{-\theta^\top x})$

$\large -log(1-g\theta(x))=log(\frac{1+e^{-\theta^\top x}}{e^{-\theta^\top x}})=log(1+e^{+\theta^\top x})$
여기서 y값에 따라 달라지는 것은 exp의 계수 부호이며 위에서 y=1와 y=-1일 때, 하나의 항만 나타내기 위해 사용한 트릭($\frac{1\pm y_i}{2}$)대신에 exp의 계수를 $y_i$로 표현할 수 있다.

그렇다면 손실함수는 더 간단히 나타낼 수 있다.

logistic function은 $h(z)=log(1+e^{-z})$이고 logistic loss는 logistic function의 평균으로 생각할 수 있다. 이것은 SVM에서 hinge loss에서 미분 불가능한 영역을 부드럽게 바꾼 형태와 같다.

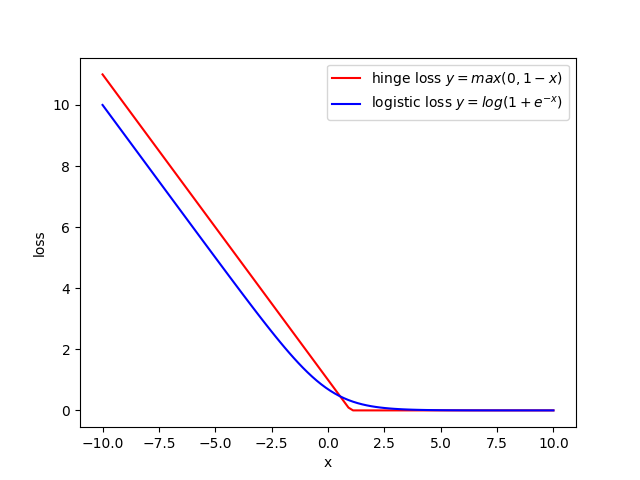
3. Multi-class classification

이진 분류에서 다중 분류로 개념을 확장해보자.

먼저 3개의 class가 있다고 가정했을 때,

• 3개의 클래스를 각각 이진 분류하는 분류기의 결합으로 표현하는 방식을 떠올릴 수 있다.
• 다른 방법으로는 각 클래스에 해당할 확률 분포로써 표현하는 방식이 있다.

사실 이진 분류기의 결합도 확률 조건(양수이며, 합이 1)을 만족하도록 변형하면 확률 분포로 표현할 수 있다.

확률 분포로 표현하는 방법은 다음과 같다.

3.1 SoftMax function

logistic function을 일반화한 것으로

exponential 꼴이기 때문에 모든 값이 양수이며, 모든 $i$에 대해 더하면 분모와 분자가 같아져 합이 1이 되어 확률 분포로 해석이 가능하다.

• Logistic Regression $\subseteq$ Softmax Regression
  
  Softmax의 특수한 케이스로 binary logistic을 포함하고 있다.

4. Confusion Matrix (False Positive, False Negative)

분류 문제에서 실제 label에 대해 예측값이 얼마나 잘 동작하는지 모델의 성능을 평가하는 지표로 정밀도(Precision), 재현율(Recall), 정확도(Accuracy)등을 사용한다.

이를 알아보기 전에 실제 정답과 예측값을 테이블 형태로 나타내보자.

• Confusion Matrix

prediction\label	Positive	Negative
Pred Positive	TP	FP
Pred Negative	FN	TN

• True Positive(TP) : 1인 정답을 1로 예측
• False Negative(FN) : 1인 정답을 0으로 예측
• False Positive(FP) : 0인 정답을 1로 예측
• True Negative(TN) : 0인 정답을 0으로 예측

4.1 평가지표

• 정확도 (Accuracy):
  전체 데이터 중 정답과 예측이 같은 정도
  계산식: $ACC=\frac{TP+TN}{TP+TN+FP+FN}$

데이터 클래스의 불균형을 설명하기 어렵다.
1과 0 의 정답 비율이 90%,10%인 경우, 임의의 학습 없이 전부 1로 예측하면 90%의 정확도를 얻는다. 이는 올바른 학습이 이루어졌다고 볼 수 없어 추가적인 지표를 살펴볼 필요가 있다.

• 정밀도 (Precision):
  모델이 양성으로 예측한 사례 중에서 실제로 양성인 비율
  계산식: $Precision=\frac{TP}{TP+FP}$

• 재현율 (Recall):
  실제 양성인 사례 중에서 모델이 양성으로 올바르게 예측한 비율
  계산식: $Recall=\frac{TP}{TP+FN}$

예시) 코로나를 식별하는 모형이 있을 때, 약간의 조짐이 있다면 코로나라고 분류하는 것은 재현율이 높아지고 정밀도는 낮게 된다. 반대로 엄격하게 코로나를 분류하는 모델은 정밀도는 높지만 재현율은 떨어질 수 있다.

정밀도와 재현율은 trade-off 관계이므로 목적에 따라 기준을 설정해주어야 한다.

만약, 두 경우 모두 적절하게 고려하고 싶다면 F1 점수를 사용한다.

F1 스코어 (F1 Score):
정밀도와 재현율의 조화 평균으로, 모델의 성능을 종합적으로 평가하는 지표
계산식: $2\frac{Precision\cdot Recall}{Precision+Recall}$

4.2 ROC curve

ROC 커브는 y축에 민감도, x축에 1-특이도(FPR)를 나타내어 다양한 분류 임계값에 대한 모델의 성능을 비교할 수 있도록 시각화한 것이다.

• 민감도(Sensitivity, Recall, True Positive Rate, TPR)
  1인 정답을 1이라고 예측한 비율
  계산식: $Sensitivity=\frac{TP}{TP+FN}$

• 특이도 (Specificity, True Negative Rate, TNR)
  0인 정답을 0이라고 예측한 비율
  계산식: $Specificity=\frac{TN}{TN+FP}$

• False Positive Rate (FPR) : 1-특이도(TNR)
  계산식: $FPR=1-\frac{TN}{TN+FP}=\frac{FP}{TN+FP}$

그림으로 나타내면 다음과 같다.

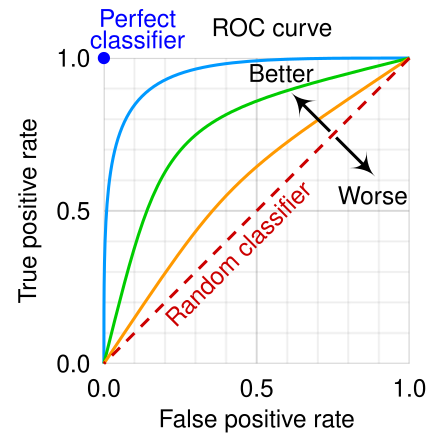Receiver operating characteristic

무작위로 예측한 경우가 붉은 점선을 따르며 이 선보다 위쪽에 놓일수록 성능이 좋다.

다음은 정답이 0과 1이 5개씩 있는 분류 문제에서 4개의 ROC를 나타낸 것이다.

y_true = np.array([0,0,0,0,0,1,1,1,1,1])
y_scores_mis0 = np.array([0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0])
y_scores_mis1 = np.array([0.1,0.2,0.3,0.4,0.6,0.5,0.7,0.8,0.9,1.0])
y_scores_mis2 = np.array([0.1,0.2,0.5,0.7,0.6,0.5,0.4,0.8,0.9,1.0])
y_scores_mis3 = np.array([0.9,0.2,0.8,0.7,0.6,0.5,0.4,0.3,0.9,1.0])

curve 0 은 0.5를 기준으로 잘 분류되며 curve 1부터 3까지는 점점 정답과 다른 예측을 한 경우이다.

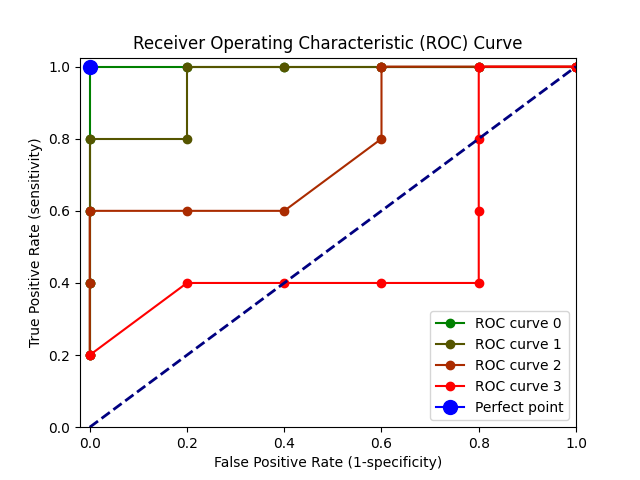
AUC (Area Under the Curve): ROC 곡선 아래의 면적을 나타내며, AUC 값이 클수록 모델의 성능이 좋다는 것을 의미한다. AUC는 0.5에서 1 사이의 값을 가지며, 1인 경우가 Perfect point에 해당(curve 0)한다.