
[혼자 공부하는 머신러닝+딥러닝] 책에 기반한 정리글입니다.
전체 소스코드는 아래 Github 링크에서 확인할 수 있습니다.
0. 개요
저번 글에서 다른 k-최근접 이웃 회귀는 샘플과 가까운 이웃들의 평균으로 값을 예측하기 때문에, 샘플이 훈련세트의 범위를 벗어나면 엉뚱한 값을 예측하는 한계가 있다.
이를 극복하기 위해 직선, 곡선을 학습하는 선형 회귀를 사용한다.
- 선형 회귀 : 모델 기반 학습
- k-최근접 이웃 회귀 : 사례 기반 학습
1. 직선 형태의 선형회귀
1-1. 선형회귀 알고리즘으로 모델 훈련하기
sklearn.linear_model 패키지의 LinearRegression 클래스를 이용한다.
#선형 회귀 알고리즘
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target)
print(lr.predict([[50]]))
#50cm 농어 값을 예측함
# 선형회귀의 그래프는 y = ax + b 꼴
print(lr.coef_, lr.intercept_) #a, b출력
[1224.64995442] 50cm 농어의 무게 예측
[37.77304367] -664.002228934682 y=ax+b 꼴의 a와 b값
여기서 y=ax+b 꼴의 직선은 무게 = a x 길이 + b 이다.
1-2. 선형회귀로 학습된 모델의 결정계수 찾기
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))출력
0.9741365873832454
0.958600635034071
훈련 세트의 결정계수가 테스트 세트의 결정계수보다 크고
테스트세트의 점수가 나쁘지 않기 때문에 적절하다.
1-3. 선형회귀로 학습된 모델의 직선 그려보기
lr객체의 coef_, intercept_ 에 a, b 가 저장되어 있다.
plt.scatter(train_input, train_target)
plt.plot([15, 50], [15*lr.coef_ + lr.intercept_, 50*lr.coef_ + lr.intercept_]) # 선형회귀 그래프
plt.scatter(50, lr.predict([[50]]), marker="^") # 50cm 농어
plt.xlabel = "length"
plt.ylabel = "weight"
plt.show()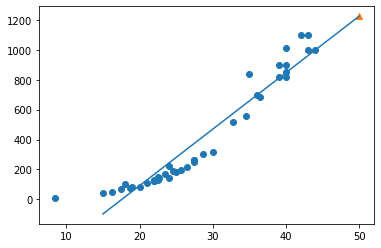
단, 그래프를 살펴보면 x값이 일정 숫자 미만으로 작아지면 y값이 음수가 되는 문제가 발생한다.
이를 해결하기 위해 최적의 곡선을 찾아본다.
2. 다항 회귀로 학습된 모델
2-1. 다항 회귀로 모델 훈련하기
2차 방정식 꼴의 그래프를 그리려면 길이를 제곱한 항이 훈련 세트에 추가되어야 한다.
# 다항 회귀, 2차 방정식 그래프
# 길이를 제곱한 항을 훈련 세트에 추가
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]])) #길이가 50cm인 농어 무게 예측
print(lr.coef_, lr.intercept_) # y = ax2 + bx + c 에서 a,b,c 값출력
[1602.09566089] 50cm의 농어 무게 예측값
[ 1.05069745 -23.1385971 ] 132.28189533175203 학습한 계수의 값
무게 = 1.05 길이^2 - 23.14 길이 + 132.28 라는 식을 학습했다.
2-2. 다항회귀 모델의 결정계수 찾기과 그래프 그려보기
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))출력
0.9741365873832454
0.958600635034071
훈련 세트의 결정계수가 테스트 세트의 결정계수보다 크고
테스트세트의 점수가 나쁘지 않기 때문에 적절하다.
2-3. 다항회귀 모델의 그래프 그려보기
# 다항회귀 그래프 그려보기
point = np.arange(15, 50)
plt.scatter(train_input, train_target)
plt.plot(point, lr.coef_[0]*point**2 + lr.coef_[1]*point + lr.intercept_)
plt.scatter(50, 1602.09, marker="^")
plt.show()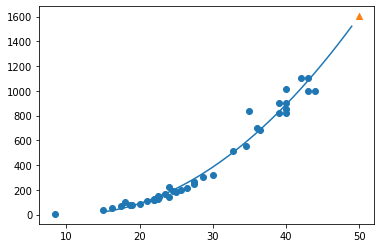
단순 선형 회귀 모델보다 나은 그래프가 그려졌다.
