- 최단 경로
-
문제의 정의
- 입력 : G = (V,E,W), 시작 노드, 도착 노드
- 출력 : 시작 노드부터 도착 노드까지의 최단 경로
- 경로는 시작 노드부터 에지를 타고 계속 연결되어 도착노드까지 이르는 에지들의 집합
- 경로의 가중치는 포함된 에지의 가중치들의 총합 -
최단경로는 사이클을 포함할 수 없다.
- 양의 가중치의 사이클이라면 돌 필요가 없고, 음의 가중치의 사이클이라면 경로의 가중치를 무한히 적게 할 수 있으므로 문제 정의 불가능하다. -
에지의 가중치가 양이면 Dijkstra's algorithm 이용
-
에지의 가중치가 음수가 가능하면 Bellman-Ford algorithm 이용
- Dijkstra 알고리즘
- 그래프의 노드를 이미 최단 거리를 알고 있는 노드들과 아직 최단 거리를 알지 못하는 노드들로 구분
- 처음에는 시작 노드만 거리를 알고 있고, 시작 노드에서 시작 노드까지 거리는 0이다.
- 차례대로 하나씩 최단 거리를 알고 있는 노드들을 늘려가기 시작한다.
- b의 노드들 중 a 에 속하는 노드들과 에지 하나로 연결된 노드들은 잠정적인 최단 거리를 알 수 있다.(직전 노드까지의 거리 + 에지의 가중치)
- 이 노드들 중, 가장 거리가 가까운 것을 고른다면 이 에지보다 더 작은 가중치를 가지고 해당 노드를 방문하는 방법은 없다.
- Prim's 알고리즘과 비슷하지만 거리의 정의가 다르다.
- 이 과정을 반복해가면서 매 시점에서 시작노드부터 거리가 가장 가까우면서 이미 최단 거리를 알고 있는 노드들에 포함되지 않은 노드를 추가해 나간다.
- 도착 노드까지의 최단 거리를 알아내면 알아내면 알고리즘 종료한다.
- 노드의 개수는 유한하므로 언젠가는 종료한다.
-ex)
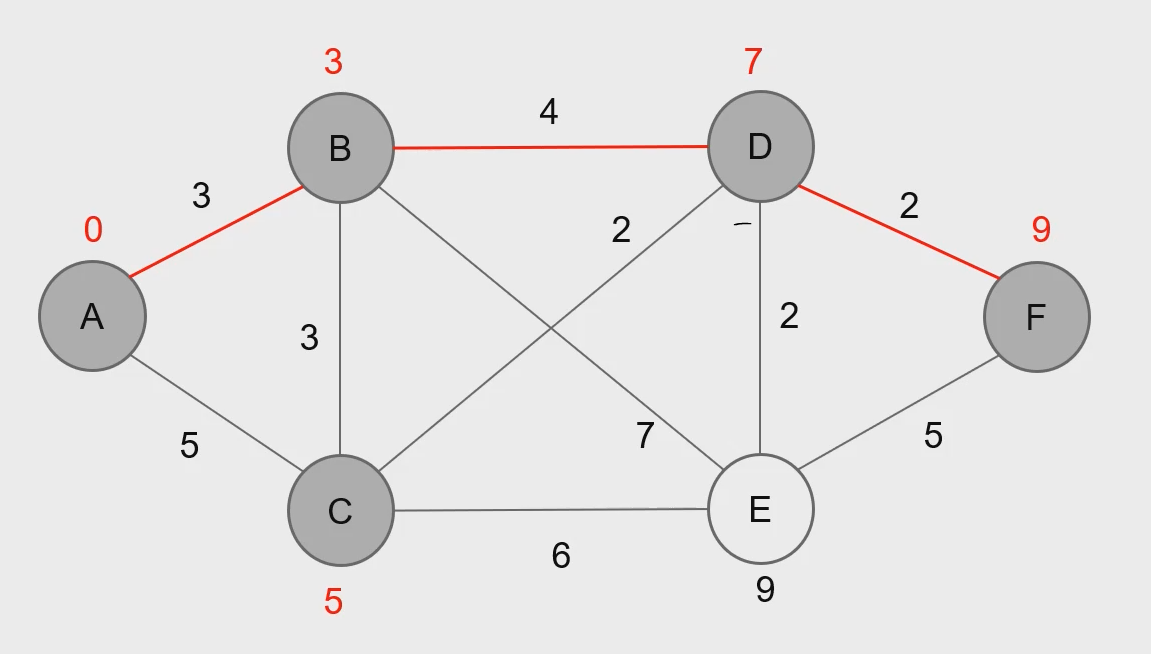
- 정확성
- 처음에는 시작 노드 - 시작노드까지 거리는 0임이 자명
- 이후 아직 최단 거리 알지 못하는 노드들 중 시작노드에서 가장 가까운 것을 최단 거리를 알고있는 노드들에 추가하면 이 노드까지 최단 거리를 알 수 있음
- 다른 노드를 통해서 이 노드를 방문할 때에는, 모든 에지의 가중치가 양 이므로 보다 더 적은 거리로 도달할 수 없다.
- 시간 분석
- 가장 간단한 구현 O(E+V^2) = O(V^2)
- 매번 최단 경로를 알게 되는 노드가 하나이므로 총 V-1번 반복- 노드 중 최단 거리인 노드를 찾는데 선형 탐색으로 최대 V 시간
- MinHeap을 이용한 구현 O(E+V)log(V)
- 에지의 한쪽 끝점의 최단 경로를 알게 된 순간 다른 노드들의 최단 거리 갱신- 노드 중 최단 거리인 노드를 찾는데 힙을 이용 log(v)시간
