- 최소신장 트리
- 신장트리 : 그래프 g의 노드 v를 모두 포함하는 e에 속하는 에지를 사용하여 만든 트리
- 최소 신장 트리 : 가중 그래프 g 의 신장트리 중에서 트리에 속한 가중치의 합이 가장 작은 신장 트리
- 신장 트리를 만드는 방법
-Prim's algorithm
-Kruskal's algorithm
- Prim's algorithm
- 한 노드에서 시작한다. 이 노드가 mst의 일부분이 된다.
- 지금까지 구한 mst의 부분에서 다른 노드들까지의 거리를 정한다.
- 에지 하나만큼 떨어진 노드들은 이 에지의 가중치가 거리
- 그 외의 노드들은 거리가 무한대이다.
- 거리를 아는 노드 중 가장 가짜운 노드를 mst에 추가
- 추가한 노드로부터 다른 노드들까지 거리를 수정한다.
- 두번째로 돌아가서 반복한다. 이 과정을 모든 노드가 mst에 추가될 때까지 반복
- ex)
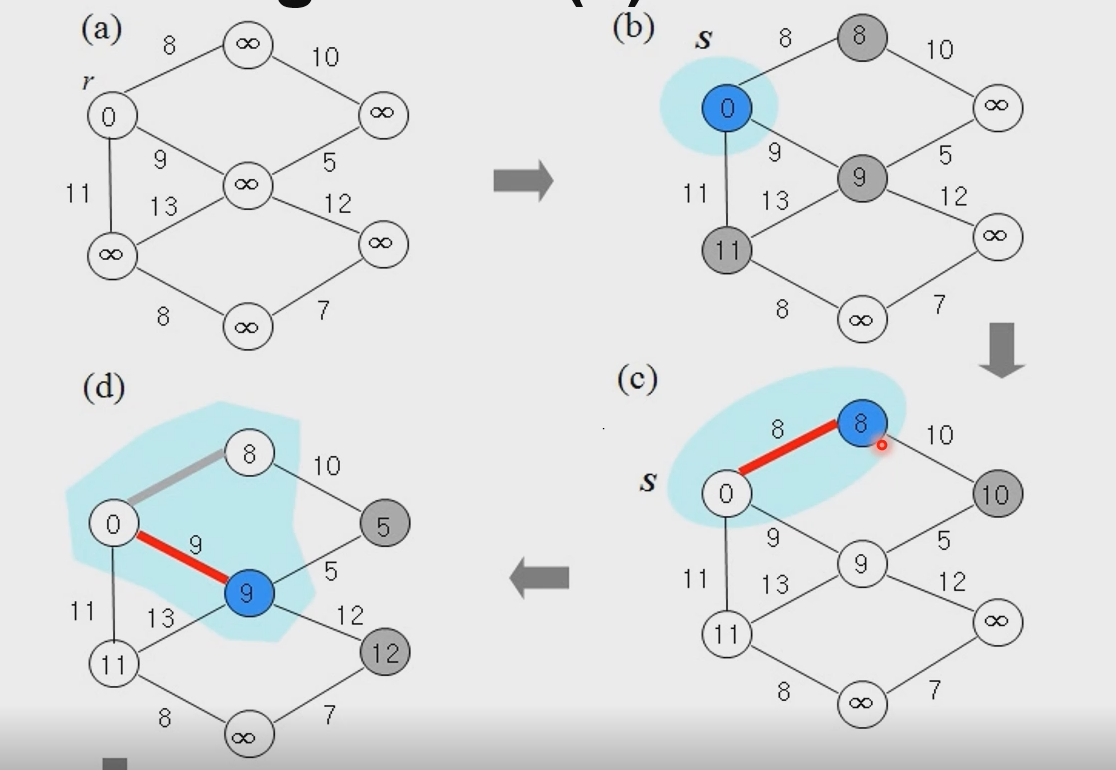
- 정확성 증명
- 처음 노드 한개로 시작하여 mst를 완성시켜나간다.
- mst는 모든 노드를 포함하므로 어느 노드에서 시작해도 된다.
- 반대로 생각했을때 v-1개의 노드로 이루어진 트리와 1개의 노드가 있다
- 이 둘을 잇는 에지는 Prim's algorithm에서 고른 에지와 같다.
- 과정을 거꾸로 올라가면 최종 노드는 1개이다.
- Kruskal's algorithm
- 노드들을 잇는 v-1개의 에지를 구하는 과정으로 볼 수 있다.
- 에지들은 가중치의 오름차순으로 정렬한다.
- 가중치가 낮은 순서부터 차례로 mst에 추가한다. 단 에지를 추가했을 때 사이클이 생기면 안된다. 이 과정을 모든 노드가 mst에 추가될 때까지 반복한다.
- 에지의 가중치의 총합은 같은 최소 신장트리가 여러개 발생할 수 있다.
- Kruskal 알고리즘 증명
- 가장 가중치가 작은 에지 e는 반드시 mst에 포함된다.
- 증명
- g = (v,E-{e})에 대해 mst를 구한 뒤 여기에 e를 추가해보자
-반드시 사이클이 생긴다. why? 이 사이클에 에지를 하나 제거하면 다시 신장트리가 생긴다.
-이 신장트리는 원래 신장 트리보다 반드시 가중치의 합이 작다.
- 에지 중 v-1개를 뽑아서 나열하는 모든 경우 고려해보자
- 이 중 사이클이 생기는 경우를 제외하고 처음으로 신장트리를 만드는 경우가 Kruskal's algorithm이 만드는 mst와 같다.
- Kruskal's algorithm 구현
- 이 에지를 추가하면 사이클이 생긴다는 것을 구현하는 법은?
- 모든 노드에 처음 서로 다른 색깔을 부여한다.
- 에지에 mst에 추가하면 , 이 에지로 이어진 부분 트리를 같은 색깔로 칠한다.
- 같은 색깔 = 같은 트리라는 뜻이므로, 같은 색을 잇는 에지를 이으면 사이클이 생긴다.
- 색깔은, 두 트리를 연결할 때 노드가 많은 쪽 트리의 색을 노드가 작은 쪽이 따라가면 O(n)번 이상 색을 칠하는 경우는 없다.

