- 탐색을 지원하는 집합을 구현하는 방법
- O(log n)보다 빨리 풀 수 있는 방법 : 해시테이블 O(n)
- 1~n 사이의 수 k 개가 원소인 집합 구현 시
- N이 무지 크다면? 메모리를 엄청 낭비하게 된다.
- 원소가 저장될 자리가 원소의 값에 의해 바로 o(1) 로 결정되는 자료 구조
- 탐색 트리의 경우, 원소의 값에 의해 결정되지만 트리를 탐색해서 내려가야한다.
- 삽입, 삭제, 검색 모두 평균 O(1)시간
- 매우 빠른 응답을 요구하는 응용에 사용된다.
- Memory paging
- 다른 연산은 지원하지 않음
- 이진 탐색 트리의 경우, 최소값, 특정값 바로 전의 값, 바로 다음의 값 등을 찾을 수 있다.
- 해시 함수를 이용하여 원소가 저장될 위치를 결정한다.
- 보통 h(x) = (ax+b) mod p 꼴
- p는 소수로, 해시 테이블의 크기와 일치
- ㄴ{25,13,16,15,7}을 저장하는 예
- h(x) = x mod 13
- 보통 해시테이블의 크기는 소수 p
- 값들을 균등하게 배분할 수 있을 수록 좋다.
- 탐색
- 주어진 해시 테이블에서 특정한 값을 찾는 경우
- 해당 해시 수식을 사용하여 접근하여 값 확인
- 한칸에 두 값이 들어있는경우 해결방법은 ? (ex) 29-> 3인데 이미 값이 있음)
- 충돌
- 해시체인 : 키들을 연결 리스트로 저장하는것
- headnode '3'에 이어진 list에 붙히는 것( 16->29)
- 해시체인은 13개 이상의 수도 저장할 수 있다. 노드 하나의 체인이 너무 길어지면 좋지 않음 성능이 발생한다. 해시는 성능이 매우 중요한 알고리즘(<log(n)
- 선형 조사
-
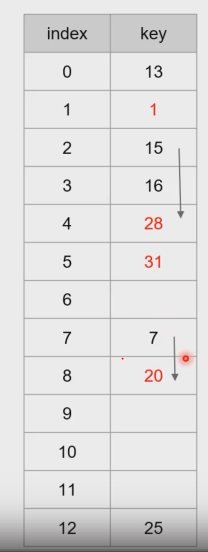
- ㄴ사용하려는 칸이 이미 차 있으면 다음칸, 다음칸을 사용하는 것
- hi(x) = (h(x)+i) mode m (i는 충돌 횟수)
- 일차군집
- 특정 영역에 원소들이 몰리는 경우- 상관없는 값을 읽고 비교하게 된다.
- 해시의 효율을 낮춘다.
- 충돌시 칸이 연속적으로 비어있지 않으면 다음칸을 계속 봐야하기 때문
- 이차원 조사
- hi(x) = (h(x)+i^2) mod m- 빈칸이 나올 때까지 다음 칸으로
- 제곱 수만큼 칸을 이동하여 배치, 몰림을 어느정도 방지(1,4,9..칸이동하여 비었다면 해당 수를 배치)
- 계속 충돌이 벌어지는 문제점이 발생
- 이중 해싱
- 이차 군집을 막기 위해, 똑같은 칸 만큼 이동하는 대신 또다른 해시 함수 f(x)이용- hi(x) = (hi(x)+if(x)) mod m
- f(x) = 1+ (x mod 11) (적어도 1은 증가, 11과 13dms tjfhth)
- 첫번째에서 충돌이 벌어져도 두번째에선 모두 다른값이 이루어지므로 삽입 가능하다.
- 삭제
- 단순히 빈칸으로 남길 수 없음
-
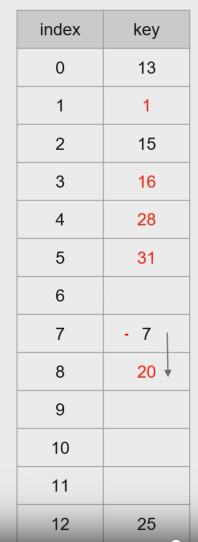
- ㄴ 3번칸에 있는 16을 지우면 어떤것이 문제일까?
- 28을 찾아갈 수 없다.
- 해결책 :단순히 지우지 않고, deleted로 표시
- 빈칸이므로 값을 쓸수는 있으며, 탐색시는 다음 값으로 계속 진행할 수 있다.
- 단순히 빈칸으로 남길 수 없음
- 검색시간
- 적재율 a = n/m(원소의 수 나누기 테이블의 크기)
- 평균적으로 해시 테이블의 한 원소당 a만큼의 원소가 있다고 생각할 수 있으므로 평균 검색시간은 1+a- a >0.5라면, 전체테이블의 절반이상이 차 있다면 일차군집이 발생할 확률이 높다.
- 해결법 : 해시 테이블의 크기를 두 배로 늘리고, 새로운 해시 함수를 사용하여 해시 테이블을 다시 만든다.
- 적재율 a = n/m(원소의 수 나누기 테이블의 크기)
백엔드 & 전공 공부