- 그리디 알고리즘
- 매 단계마다, 각 단계에서 최선이라고 볼 수 있는 선택을 하는 것
- 전체적인 입장을 보지 않고 순간 최선을 취한다.
- 알고리즘이 매우 간단한 대신, 구한 답이 정답이라는 보장은 없다.
- 정답을 알려면 증명이 필요하다.
- 기본형태
- C : 후보들의 집합
- Solution(s) : 특정한 후보들의 집합 s가 주어진 문제의 해인지 결정하는 함수
- Feasible(s) 특정 후보들의 집합 s 가 문제의 해가 될 가능성이 있는지를 결정하는 함수
- Select(s) 남아 있는 후보들의 집합 c에서 현상태에서 가장 좋은 후보를 선택하는 함수 - 회의실 배정 문제
- 한 회의실을 가지고 가장 겹치지 않게 많은 횟수의 회의를 할수 있는 프로그램
- 입력 : 첫줄 회의의 수, 둘째 줄부터 n+1줄까지 시작,종료시간 정수 쌍
- 출력 : 가능한 많은 회의의 개수
- 가능한 접근 방법
- 회의 시간이 짧은 것부터 고려해서 이미 넣은 회의와 충돌하지 않으면 넣는다.
- 정답은 두개 인데 한개밖에 넣을 수 있는 반례 발생- 다른 회의와 가장 적게 겹치는 회의부터 넣는다.
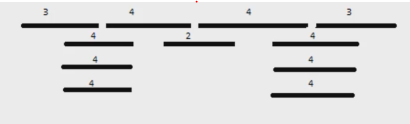
- 넣는 순간 최대 4개 가능한데 3개밖에 넣을 수 없음
- 해법 : 제일 빨리 끝나는 회의부터 넣는다.
- 다른 회의와 가장 적게 겹치는 회의부터 넣는다.
- 증명
- 회의들을 끝나는 시간에 따라 정렬하면 정답은 1을 포함하거나 포함하지 않거나 둘 중 하나이다.- 정답이 1을 포함하지 않는다면
- 정답의 첫번째 답이 1과 겹치지 않는다면, 1을 넣어서 답을 하나 더 길게 만들 수 있으므로 모순- 정답의 첫번째 답이 1과 겹친다면, 첫번쨰 답은 1보다 늦게 끝나므로, 이를 빼고 1을 넣으면 여전히 답이 된다.
- 따라서 정답은 반드시 1을 포함한다. 이제 1을 제외한 나머지 구간에 대해서 답을 구하면 된다.
- 정답이 1을 포함하지 않는다면
- 이집트 나눗셈 문제
- 유리수 p/q가 주어지면, 분자가 1인 분수들의 합으로 p/q를 표현하시오.
- 해법 1 : n = 2,3,...해보면서 1/n과 p/q중 어느수가 더 큰지 생각해 보면서 1/n이 더 크다면 n := n+1, 아니면 p/q = p/q-1/n로 계속 문제를 풀어 p/q가 0이 되면 종료
- 해법 1은 만약 p/q가 분자가 1인 분수들의 합으로 표현할 수 있다면 정답을 낼 수 있다. 분모의 값이 매우 크다면 비효율적이다.
- 해법 2 : p/q에 대해서 이 수의 역수 q/p와 같거나 큰 가장 작은 정수 q/p를 찾고, 1/[q/p]를 p/q에서 뺀다. 이 과정을 0이 될 때까지 반복
백엔드 & 전공 공부