[TIL]정렬 알고리즘

순 번	정렬 방법	BigO(Best)	BigO(Avg)	BigO(Worst)
1	버블 정렬(Bubble Sort)	O(n)	O(n^2)	O(n^2)
2	선택 정렬(Selection Sort)	O(n^2)	O(n^2)	O(n^2)
3	삽입 정렬(Insertion Sort)	O(n)	O(n^2)	O(n^2)
4	병합 정렬(Merge Sort)	O(n log n)	O(n log n)	O(n log n)
5	퀵 정렬(Quick Sort)	O(n log n)	O(n log n)	O(n^2)
6	힙 정렬(Heap Sort)	O(n log n)	O(n log n)	O(n log n)
7	계수 정렬(Counting Sort)	O(n + k)	O(n + k)	O(n + k)
8	기수 정렬(Radix Sort)	O(nk)	O(nk)	O(nk)
9	쉘 정렬(Shell Sort)	-	각각 다름	O(n^2)

위는 대표적으로 사용되는 정렬 방식이다.

---

1. 버블 정렬(Bubble Sort)

: 인접한 두 요소를 비교하여 더 큰 요소를 뒤로 보내는 방식으로 정렬한다. 개인적으로는 비누방울을 불면 하늘로 날아가듯 거품(Bubble)이 크면 위로 올라간다. 이렇게 외웠던 것 같다.

#include <stdio.h>

// 버블 정렬 함수
void bubbleSort(int arr[], int n) {
    int i, j, temp;
    int swapped;

    for (i = 0; i < n-1; i++) {
        swapped = 0; // 정렬이 완료되었는지 체크하기 위한 플래그

        // 마지막 i개의 요소는 이미 정렬되어 있으므로 비교할 필요 없음
        for (j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                // 인접한 두 요소를 비교하여 더 큰 요소를 뒤로 보냄
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
                swapped = 1; // 요소를 교환했음을 표시
            }
        }

        // 만약 교환이 한 번도 이루어지지 않았다면 리스트가 정렬된 상태임
        if (swapped == 0)
            break;
    }
}

---

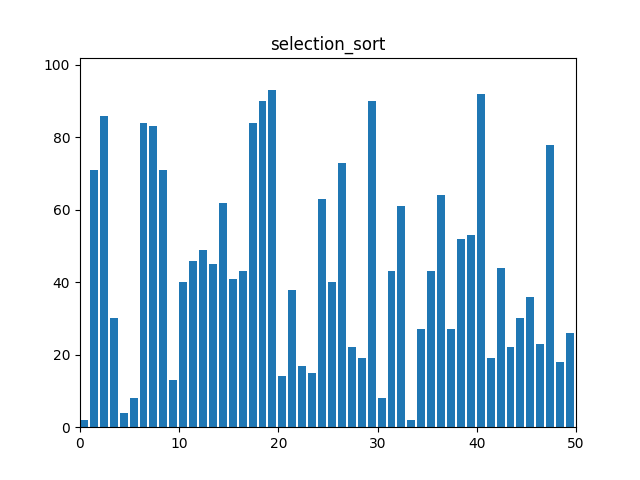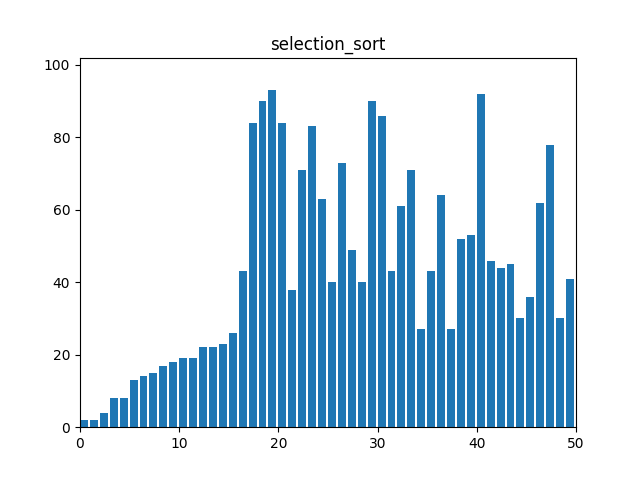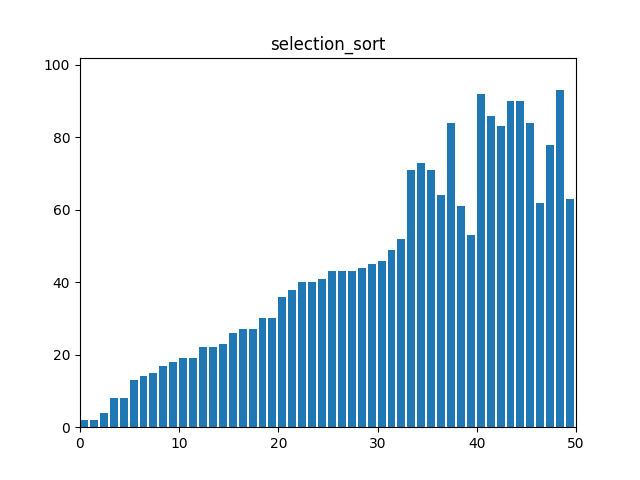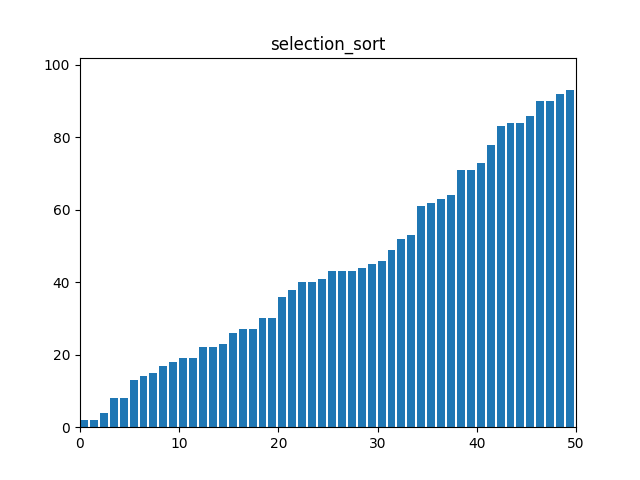
2. 선택 정렬(Selection Sort)

: 각 단계에서 리스트의 최소값을 찾아 정렬되지 않은 부분의 첫 번째 요소와 교환한다.

#include <stdio.h>

// 선택 정렬 함수
void selectionSort(int arr[], int n) {
    int i, j, minIdx, temp;

    for (i = 0; i < n-1; i++) {
        minIdx = i; // 현재 구간에서 가장 작은 값의 인덱스

        // 나머지 요소들 중에서 최소값 찾기
        for (j = i+1; j < n; j++) {
            if (arr[j] < arr[minIdx]) {
                minIdx = j;
            }
        }

        // 찾은 최소값을 현재 구간의 첫 요소와 교환
        temp = arr[minIdx];
        arr[minIdx] = arr[i];
        arr[i] = temp;
    }
}

---

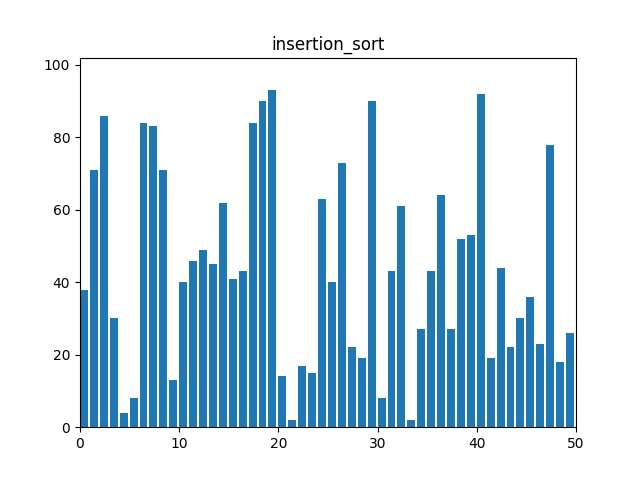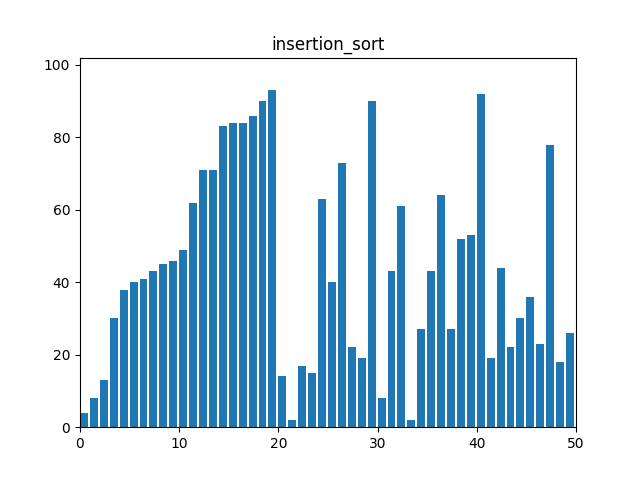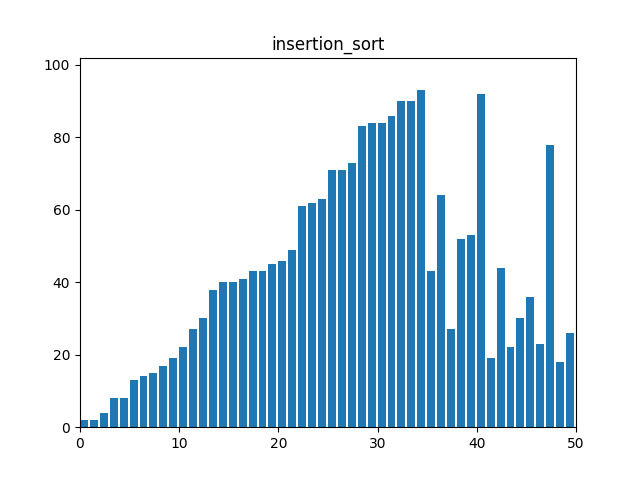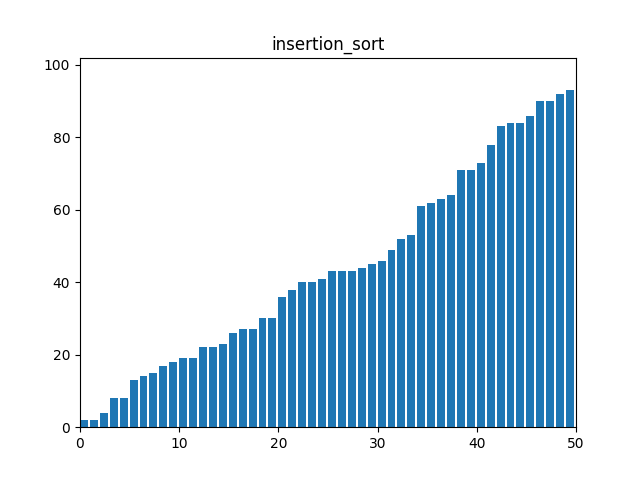
3. 삽입 정렬(Insertion Sort)

: 정렬된 부분과 정렬되지 않은 부분으로 리스트를 나누어, 정렬되지 않은 부분의 첫 번째 요소를 정렬된 부분의 적절한 위치에 삽입한다. 정렬되지 않은 요소 하나씩 돌면서 정렬된 쪽에서 있어야 할 자리에 넣는 식이다.

#include <stdio.h>

// 삽입 정렬 함수
void insertionSort(int arr[], int n) {
    int i, key, j;

    for (i = 1; i < n; i++) {
        key = arr[i]; // 현재 삽입될 요소
        j = i - 1;

        // key보다 큰 요소들을 한 칸씩 뒤로 이동
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key; // key를 올바른 위치에 삽입
    }
}

---

4. 병합 정렬(Merge Sort)

: 분할 정복(Devide and Conquer) 기법을 사용, 리스트를 재귀적으로 분할 후 병합하여 정렬한다. 리스트를 나누고 정렬한 후 병합한다.

#include <stdio.h>
#include <stdlib.h>

// 병합 함수
void merge(int arr[], int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;

    int* L = (int*)malloc(n1 * sizeof(int));
    int* R = (int*)malloc(n2 * sizeof(int));

    for (int i = 0; i < n1; i++)
        L[i] = arr[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[mid + 1 + j];

    int i = 0, j = 0, k = left;

    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }

    free(L);
    free(R);
}

// 병합 정렬 함수
void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;

        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);

        merge(arr, left, mid, right);
    }
}

---

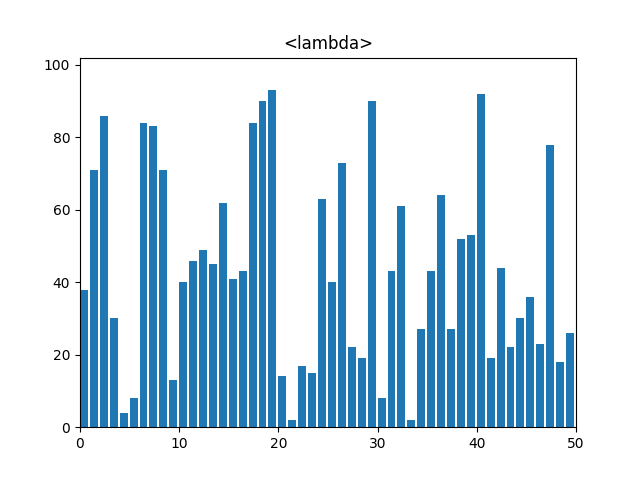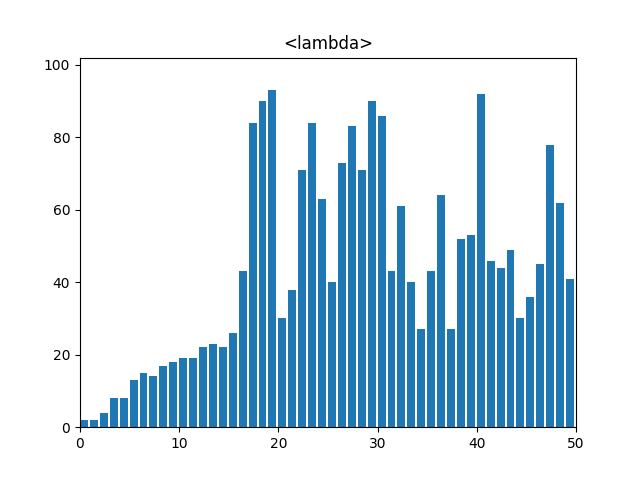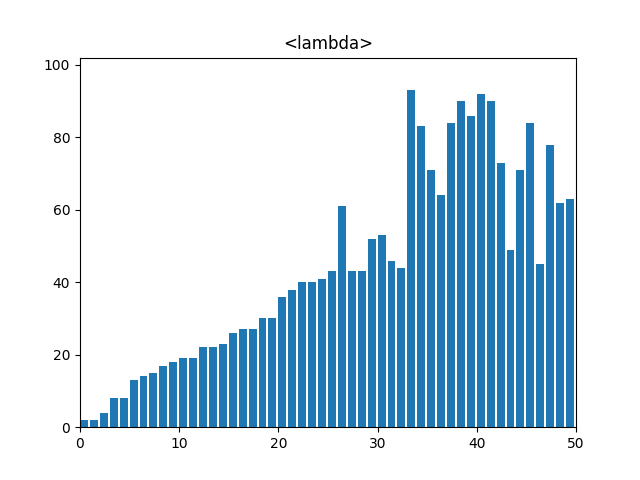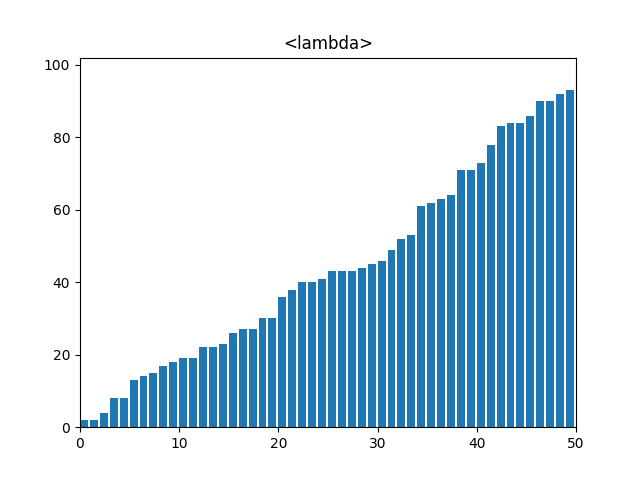
5. 퀵 정렬(Quick Sort)

: 분할 정복 기법을 사용하여 리스트를 재귀적으로 정렬, 피벗(pivot)을 선택하고 피벗보다 작은 요소와 큰 요소로 리스트를 분할한 뒤 각각을 재귀적으로 정렬한다.

#include <stdio.h>

// 피벗 기준으로 분할하는 함수
int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);
    int temp;

    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            // arr[i]와 arr[j]를 교환
            temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    // 피벗을 올바른 위치에 삽입
    temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;

    return (i + 1);
}

// 퀵 정렬 함수
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

---

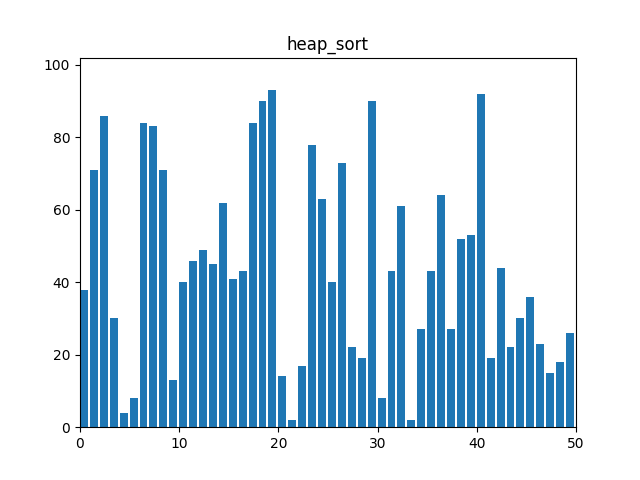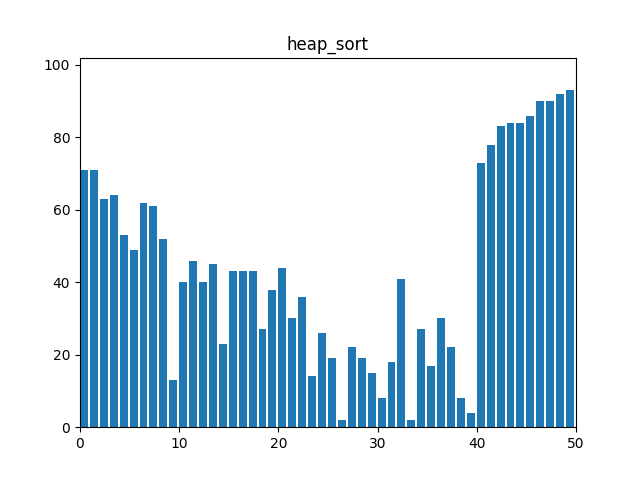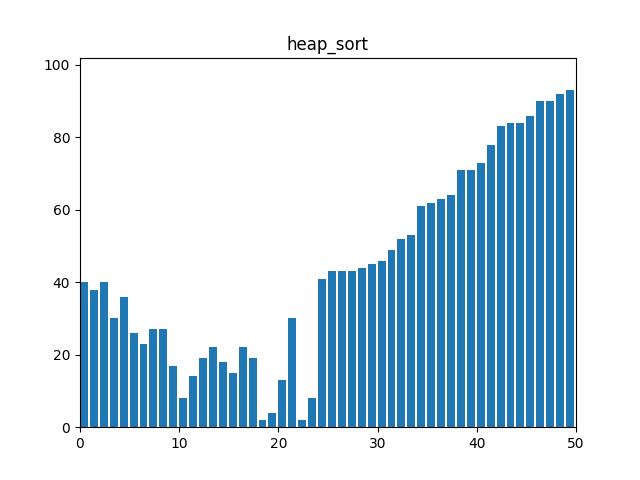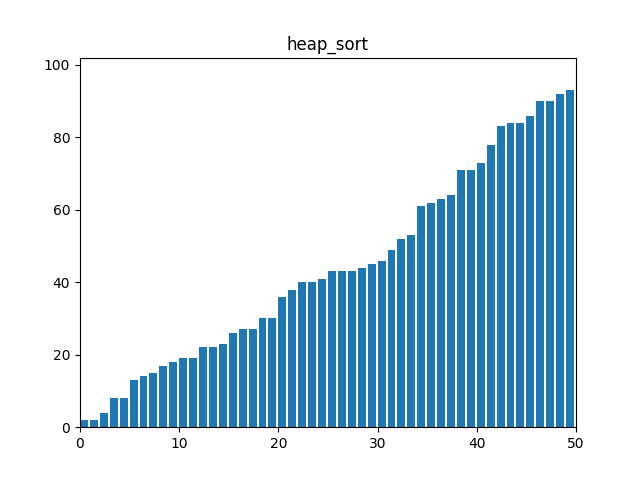
6. 힙 정렬(Heap Sort)

: 힙(Heap) 자료 구조를 이용하여 정렬한다. 최대 힙을 구성한 후, 루트 노드를 제거하고 나머지 힙을 다시 최대 힙으로 만드는 과정을 반복한다.

#include <stdio.h>

// 힙 정렬에서 힙을 재구성하는 함수
void heapify(int arr[], int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int temp;

    // 왼쪽 자식이 루트보다 클 경우
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // 오른쪽 자식이 현재 가장 큰 요소보다 클 경우
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 가장 큰 요소가 루트가 아닌 경우, 교환 후 힙을 재구성
    if (largest != i) {
        temp = arr[i];
        arr[i] = arr[largest];
        arr[largest] = temp;

        heapify(arr, n, largest);
    }
}

// 힙 정렬 함수
void heapSort(int arr[], int n) {
    // 힙을 구성
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // 요소를 하나씩 힙에서 추출
    for (int i = n - 1; i >= 0; i--) {
        // 루트(가장 큰 요소)와 마지막 요소를 교환
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;

        // 나머지 힙을 재구성
        heapify(arr, i, 0);
    }
}

---

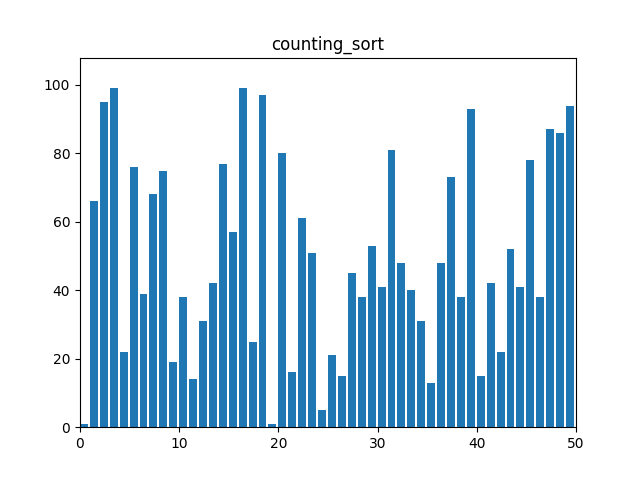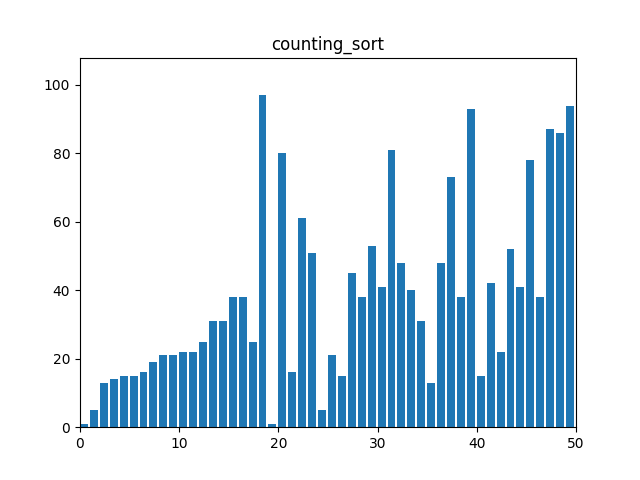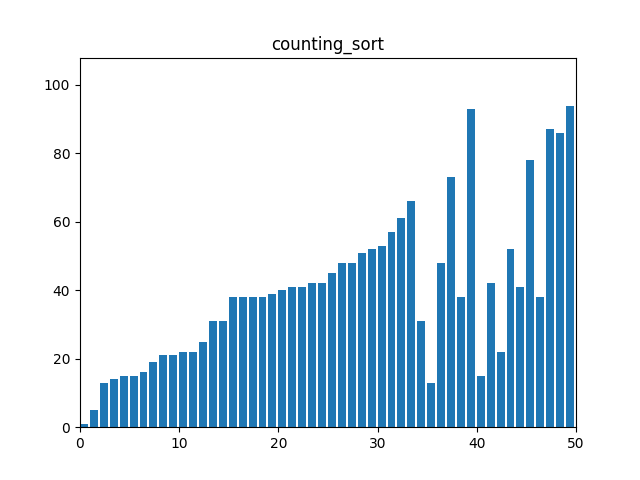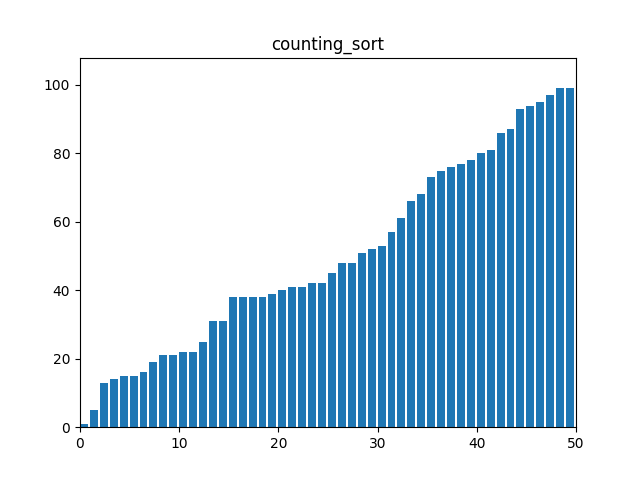
7. 계수 정렬(Counting Sort)

: 데이터의 크기 범위가 한정된 경우에 유리한 정렬 알고리즘, 각 요소의 출현 빈도를 카운트하여 정렬한다. 음수의 경우 예외 처리가 필요하다.

#include <stdio.h>
#include <string.h>

// 계수 정렬 함수
void countingSort(int arr[], int n) {
    int output[n];
    int max = arr[0];
    int min = arr[0];

    // 배열에서 최댓값과 최솟값 찾기
    for (int i = 1; i < n; i++) {
        if (arr[i] > max)
            max = arr[i];
        if (arr[i] < min)
            min = arr[i];
    }

    int range = max - min + 1;
    int count[range];
    memset(count, 0, sizeof(count));

    // 각 요소의 빈도 카운트
    for (int i = 0; i < n; i++) {
        count[arr[i] - min]++;
    }

    // 누적합 계산
    for (int i = 1; i < range; i++) {
        count[i] += count[i - 1];
    }

    // 정렬된 배열 생성
    for (int i = n - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
    }

    // 정렬된 결과를 원래 배열에 복사
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}

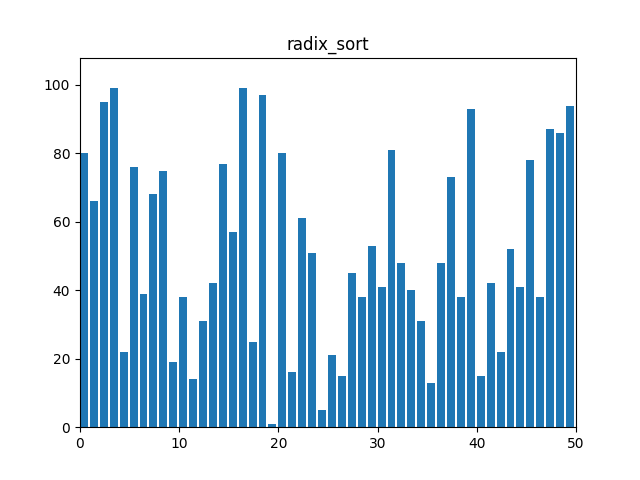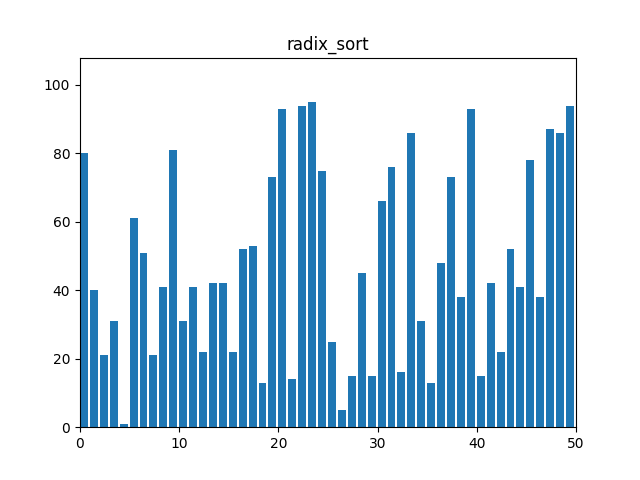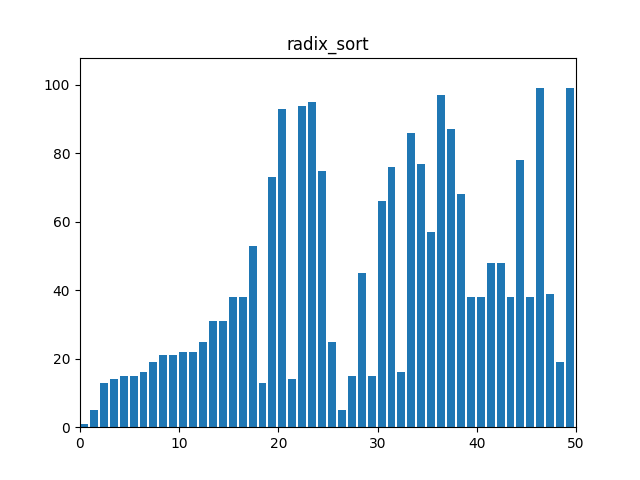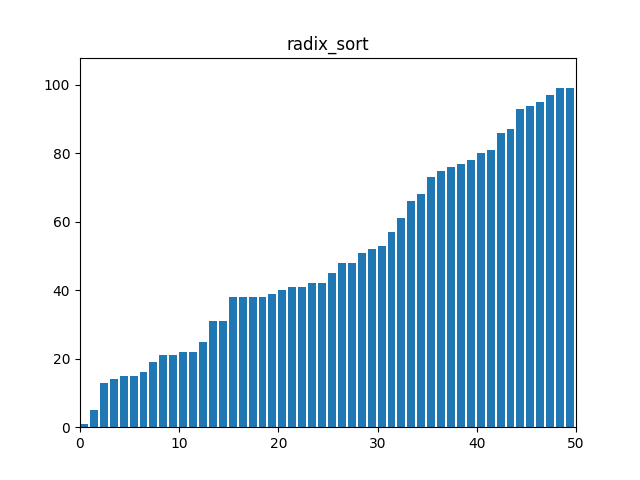
8. 기수 정렬(Radix Sort)

: 정수나 문자열 등의 데이터를 자릿수나 문자 순서대로 정렬하는 방식. 각 자리수에 대해 안정적인 정렬 알고리즘을 적용하여 정렬

#include <stdio.h>

// 최대 값을 찾는 함수
int getMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++)
        if (arr[i] > max)
            max = arr[i];
    return max;
}

// 계수 정렬을 자릿수에 따라 수행하는 함수
void countSort(int arr[], int n, int exp) {
    int output[n];
    int count[10] = {0};

    // 자릿수에 따른 빈도수 계산
    for (int i = 0; i < n; i++)
        count[(arr[i] / exp) % 10]++;

    // 누적합 계산
    for (int i = 1; i < 10; i++)
        count[i] += count[i - 1];

    // 정렬된 배열 생성
    for (int i = n - 1; i >= 0; i--) {
        output[count[(arr[i] / exp) % 10] - 1] = arr[i];
        count[(arr[i] / exp) % 10]--;
    }

    // 정렬된 결과를 원래 배열에 복사
    for (int i = 0; i < n; i++)
        arr[i] = output[i];
}

// 기수 정렬 함수
void radixSort(int arr[], int n) {
    int m = getMax(arr, n);

    // 모든 자릿수에 대해 정렬 수행
    for (int exp = 1; m / exp > 0; exp *= 10)
        countSort(arr, n, exp);
}

---

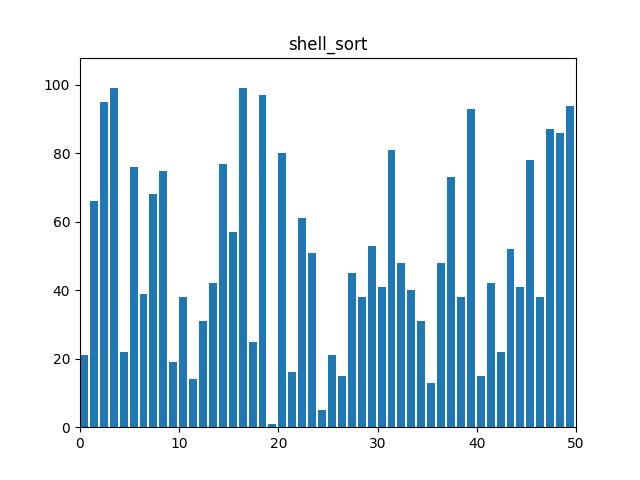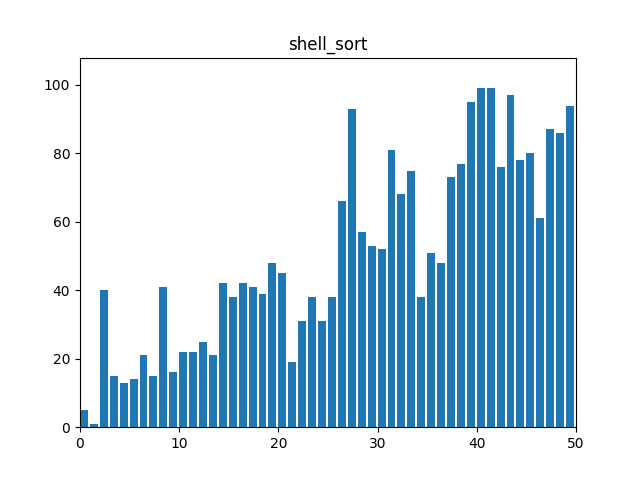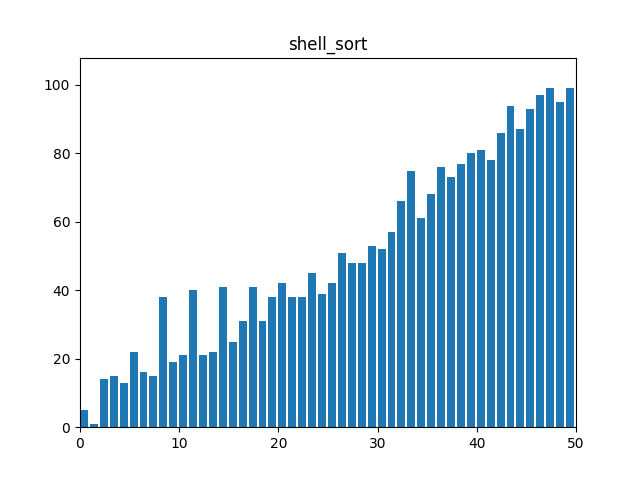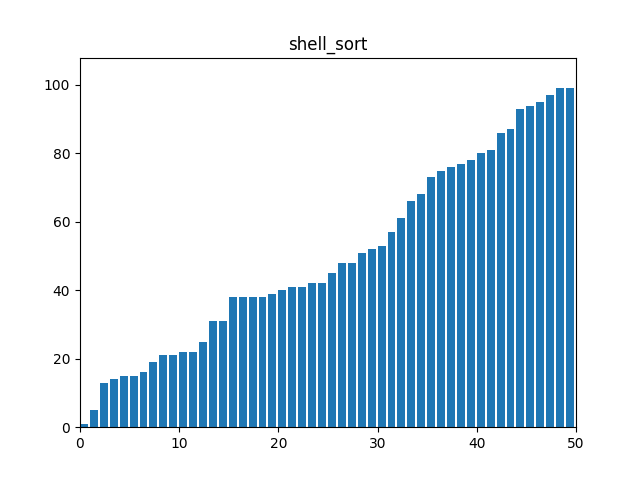
9. 쉘 정렬(Shell Sort)

: 삽입 정렬(Insertion Sort)의 일반화 버전으로, 주어진 간격으로 배열의 요소들을 비교하여 정렬한다. 간격을 점차 줄여나가면서 정렬하고 마지막 간격은 간격이 1이 되어 삽입 정렬가 동일하다.

#include <stdio.h>

// 쉘 정렬 함수
void shellSort(int arr[], int n) {
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            int temp = arr[i];
            int j;
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}