Q-Learning

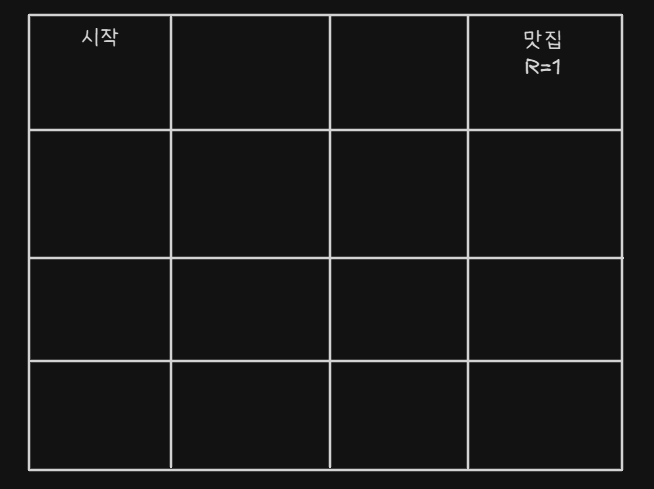
• 내 AI Agent가 맛집을 찾아가게 하고 싶은 상황이다
• 뭐 랜덤으로 움직이다가 맛집으로 들어갈 수도 있겠지
• 어쨋든 찾아가게 하고 싶다

Greedy Action

• 각 방향에 대해 점수를 부여한다
• 각 셀에서는 위, 아래, 왼쪽, 오른쪽으로 갈 수 있다(모서리 제외)
  
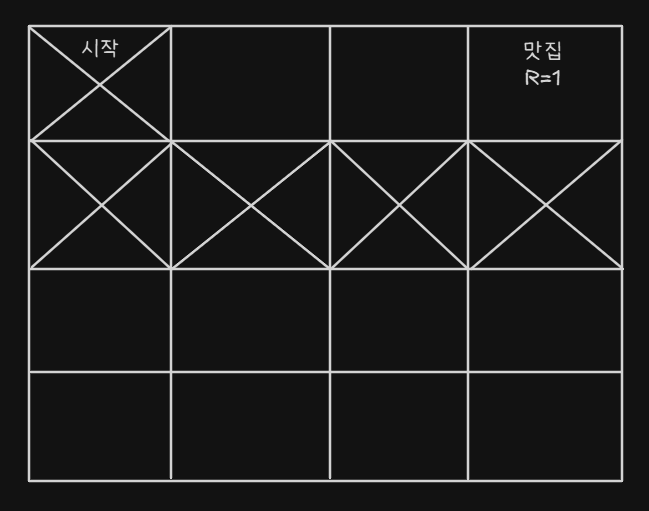
• 맛집에 들어가면 R(Reward) 보상을 받게 된다
• 계속 랜덤하게 움직이다가 어쩌다 보니 맛집으로 들어간다
  
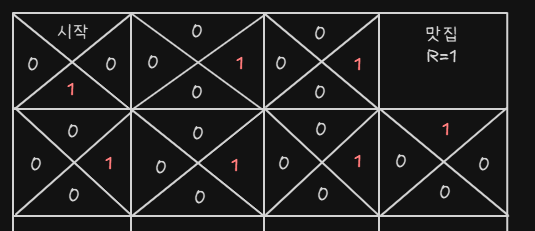
• 그럼 그 방향으로 갔더니 보상이 지급되었으니까 그 방향의 Q-value를 1로 업데이트한다
  
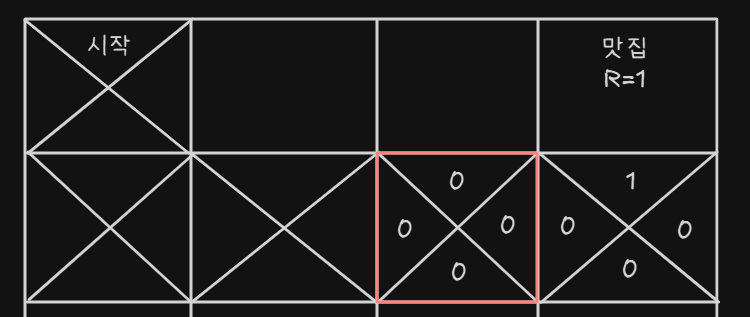
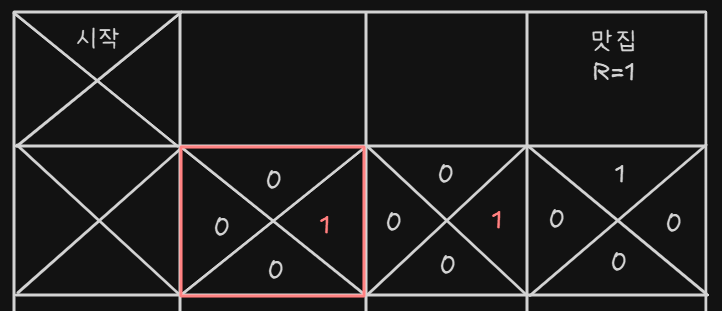
• 그 다음 에피소드에서 빨간 테두리에 있다고 가정해보자 위, 아래, 왼쪽 그리드는 값이 모두 없지만 오른쪽은 다르다, 오른쪽에서 가장 큰 값은 1이다.
• 빨간 테두리 안의 오른쪽에도 오른쪽 셀의 가장 큰 값인 1로 업데이트 한다

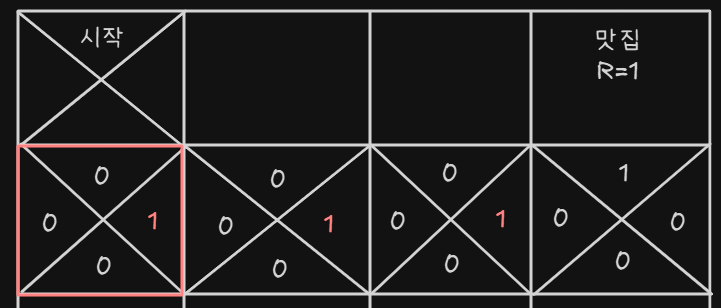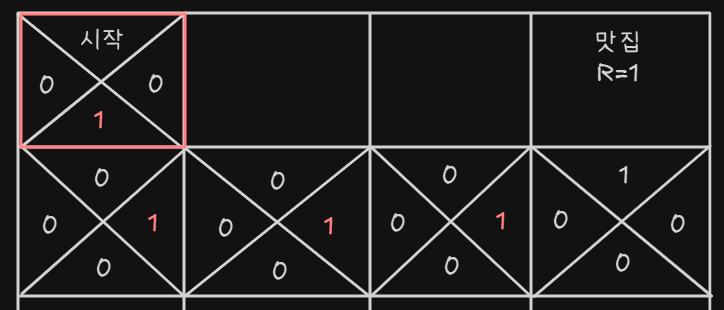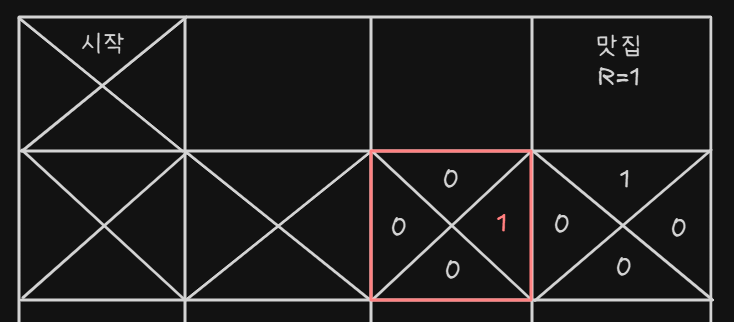
• 나머지도 똑같이 업데이트 한다
• 완성된 지금부터는 Q-value가 가장 큰 쪽으로 Greedy Action을 수행할 것이다.
• 모든 수행 결과는 동일할 것이다
• 하지만 이 결과가 최적인가? 바로 오른쪽으로 가면 더 최단 거리일텐데

Epsilon-Greedy

$\epsilon\text{-greedy},\;\epsilon\sim(0,1)$

• $\epsilon$ 값에 따라 Random Action을 하자
• Exploration : 새로운 전략을 탐험
  • 새로운 Path를 찾을 수 있다
  • 새로운 맛집을 찾을 수 있다
• Exploitation : 최적 행동을 수행
  
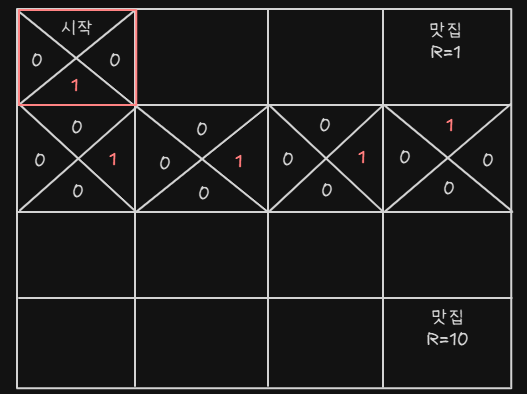
• Exploration이 없다면 평생 새로운 맛집은 못가고 가던 곳만 갈것이다.
• 하지만 계속 랜덤 행동을 한다면 최적 전략에서는 멀어질 수 있다
• 따라서 Decaying하는 $\epsilon$ 값을 활용한다
  
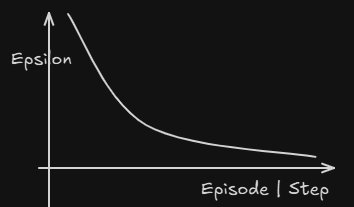
• 적절히 탐험을 하다가 나중에는 덜 탐험을 하는 식으로 Agent가 행동할 것이다
  
• 그렇게 우린 새로운 최단 거리 경로를 찾았다.
• 하지만 우리 Agent는 어디가 더 좋은 경로인지 알지 못한다.
• 위나 아래나 Q-value가 똑같으니까...

Discount Factor

• Discount factor : $\gamma$ 는 0보다 크고 1보다 작은 값이다
  위와 같이 Discount factor를 적용하면
  
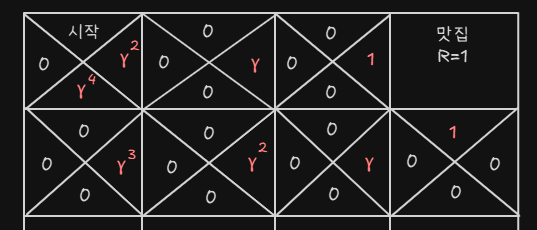
• 이런식으로 첫번째 시작점에서 $\gamma^2 >\gamma^4$ 이기 때문에 Agent는 오른쪽을 선택할 것이다
• 따라서 이 Discount rate는
  • 효율적인 Path 탐색을 할 것이며
  • 현재와 미래의 Reward에 대해 얼마나 비중을 둘 것인지 정할 수 있다

Q-value Update

• 화살표 왼쪽의 Q-값을, 화살표 오른쪽의 값으로 업데이트를 해라
• $\alpha$는 0~1의 값 : 새로운 걸 얼마나 받아들일건지?
• $(1-\alpha)Q(s_t,a_t)$ : 이쪽은 원래 가지고 있던 Q-value
• $\alpha(R_t+\gamma\max_{a_{t+1}}Q(s_{t+1},a_{t+1}))$ : 새로 업데이트 하려는 값

원본 출처[혁펜하임 유튜브] : https://www.youtube.com/watch?v=3Ch14GDY5Y8&list=PL_iJu012NOxehE8fdF9me4TLfbdv3ZW8g&index=2