
본 게시물은 고려대학교 스마트생산시스템 연구실 2023년 동계 신입생 세미나 활동입니다.
Michigan 대학의 Justin Johnson 교수님의 강의를 공부하는 형식입니다.
관련 유튜브 영상은 여기에서 확인 가능합니다.
Lecture 10: Training Neural Networks I 강의에서는 배울 수 있는 내용은 다음과 같습니다.
- Activation Functions
- Data Preprocessing
- Weight Initialization
- Regularization

Lecture 10은 신경망을 학습할 때 더욱 잘 학습하기 위해서 사용하는 추가적인 기법들에 대한 내용입니다.
학습을 하기전에 One time setup 하여 학습을 더욱 잘하도록 하는 기법들에 대해서 이번 Lecture 10에서 다루고 Lecture 11에서는 학습을 하는 도중, 학습 종료 후 성능을 높이기 위한 기법들을 배울 예정입니다.
Activation Functions
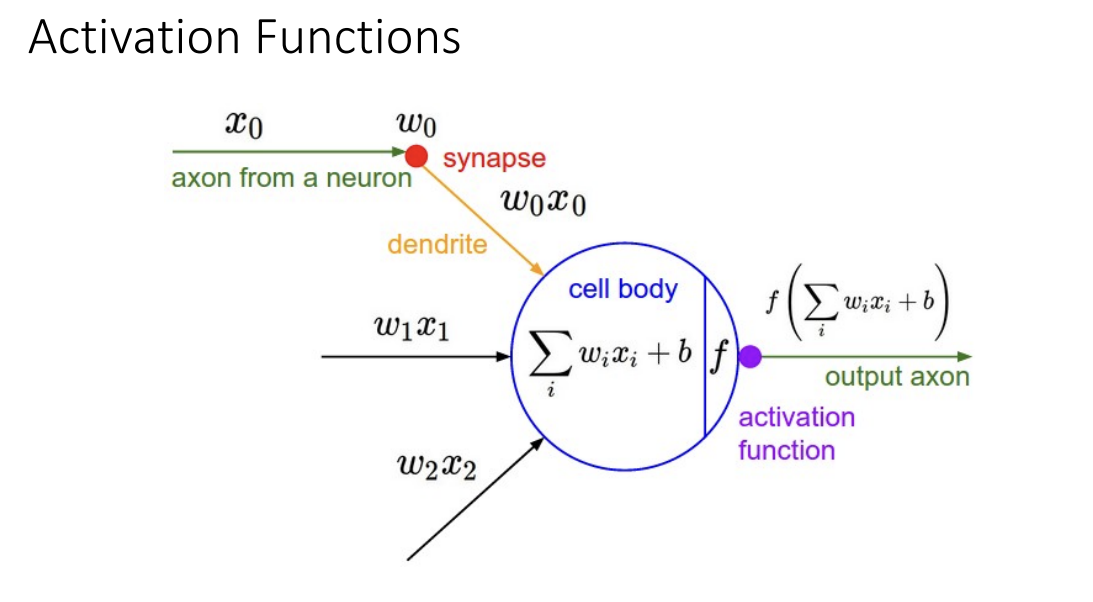
첫번째로 나오는 기법은 활성화 함수입니다.
앞선 강의에서 활성화 함수에 대한 논의는 계속해서 이뤄졌습니다.
input에 Weight을 곱하고 bias를 더해서 Output을 산출하기 전에 Deep한 구조의 효과를 보기 위해서
비선형 활성화 함수를 추가하는 것이 일반적이라는 것을 배웠습니다.

앞선 강의에서는 간단하게만 살펴보고 넘어갔었는데, 이번 강의에서는 활성화 함수 하나하나에 대해서 자세히 알아보는 시간을 가졌습니다.

먼저 시그모이드 함수입니다.
해당 활성화 함수는 input 값을 0과 1 사이의 값으로 바꿔주는 역할을 수행합니다.
0과 1 사이의 값으로 산출하기 때문에 확률로서 해석할 수 있고 이는 다시 표현해서
뉴런의 "firing rate" 입니다.
시그모이드 함수는 하지만 3가지 critical한 문제점이 존재합니다.

첫번째 문제점은 0과 멀리 떨어진 flat regimes의 경우 gradient가 거의 0이 되기 때문에 학습이 더이상 이뤄지지 않는다는 문제입니다.
해당 경우 local gradient가 0이 되기 때문에, Upstream gradient가 무엇이던간에 Downstream gradient가 0이 산출되는 문제가 존재하고 이는 역전파시 더이상 gradient가 Update 되지 못하는 상황을 연출하게 됩니다.

두번째 문제점은 시그모이드 함수의 산출물이 zero-centered 되어 있지 않다는 점입니다.
시그모이드 함수의 생김새만 봐도 0으로 centered 되어 있지는 않고 0.5에 centered 되어 있는 것을 알 수 있습니다.
이게 왜 문제가 되냐면 Local gradient가 언제나 Positive가 되기 때문에
Positive 혹은 Negative의 Scalar 값으로 전달되는 Upstream gradient가 곱해져서 Downstream gradient가 항상 Positive 혹은 Negative 값만 같도록 최적화가 이뤄진다는 점입니다.
이를 시각적으로 표현해보면 위 그림처럼 지그재그한 형태가 됩니다.
위 그림만 보면 문제가 되지 않을 것 같지만 차원이 높아진다고 생각해보시면 이는 학습이
효과적이지 못하게 이뤄진다는 것을 유추해볼 수 있습니다.
그래도 두번째 문제점은 다행히 Minibatch를 사용해서 어느 정도는 완화할 수 있다고 합니다.
마지막 문제점은 시그모이드 함수 식에 포함된 exponential 함수가 계산량이 많다는 점입니다.

다음으로 설명된 활성화 함수는 tanh 함수입니다.
생긴 것만 봐도 시그모이드 함수랑 유사한 걸 알 수 있습니다.
더 좋은 점은 zero-centered되어 두번째 문제점은 해결한 것을 알 수 있습니다.
하지만 여전히 0과 먼 지점은 flat regimes여서 gradient가 0이 되어 학습이 이뤄지지 못한다는 문제가 있습니다.

다음은 그 유명한 ReLU 함수입니다.
앞서 본 두 함수들과는 달리 양수 부분에서는 saturate 되지 않습니다. 즉 gradient가 0이 되어 학습이 안되는 현상은 없다는 것입니다.
게다가 계산적으로도 효율적입니다. 음수는 0, 양수는 그대로 내보내면 되기 때문에 구현도 쉽고 계산도 쉽습니다. 실제로도 시그모이드/tanh 함수보다 훨씬훨씬 빠르게 수렴합니다.
물론 ReLU도 단점은 있습니다.
zero-centered 되지 않았다는 점입니다. 항상 positive 또는 negative 하게 gradient가 학습되기는 하지만 이는 Minibatch를 사용해서 어느 정도는 완화 가능합니다.

그보다 더 큰 문제는 바로 Dead ReLU 문제입니다.
위 예시를 보시면 x=-10, x=0 일 때 모두 gradient가 0이 됩니다.
양수 일때만 gradient가 1이고 나머지일때는 항상 0이 되어서 학습이 전혀 이루어지지 않게됩니다.
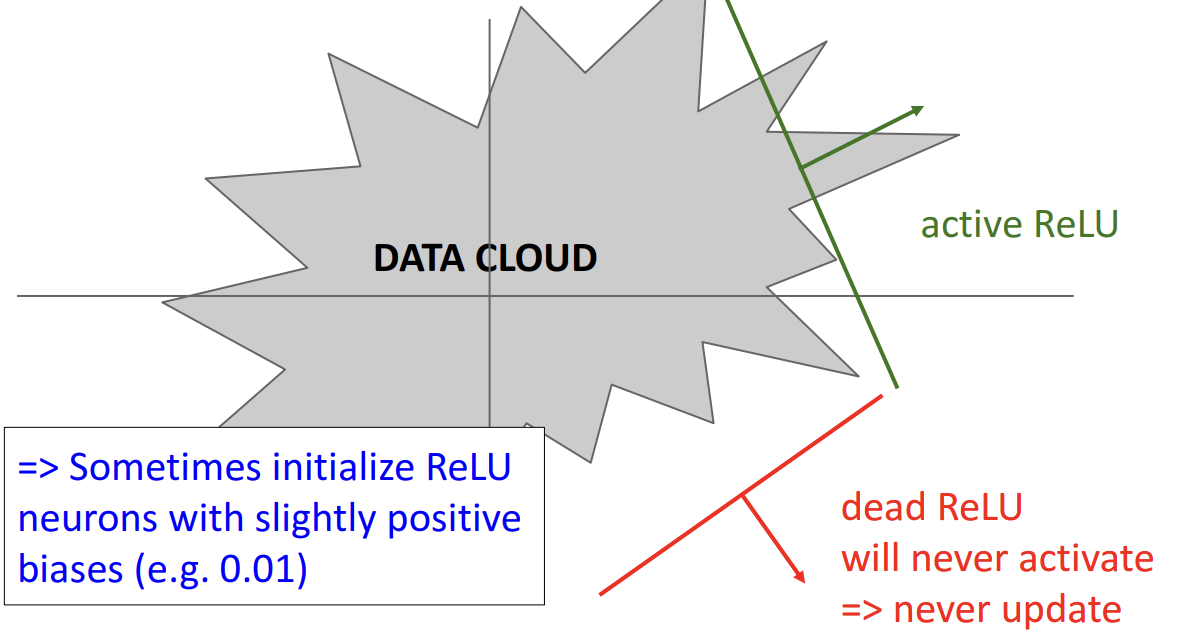
따라서 ReLU를 음수일 때 0이 아니라 아주 작은 양수 bias로 초기화하는 방법에 대해서도 고민되었습니다.

해당 아이디어를 구현한 것이 Leaky ReLU 입니다.
함수 식을 보시면 음수 일 때 0이 아니라, 0.01x 값이 나오도록 식을 구성했습니다.
이렇게 함수를 구성하면 ReLU의 장점이었던 saturate 되지 않는다는 점을 유지하고, 효율성도 그대로 유지 가능합니다.
게다가 학습이 죽어버리는 현상도 극복했습니다!
하나 고민해봐야할 점은 0.01 값만 곱해줘야하나? 입니다. 이는 사실 하이퍼파라미터입니다.
따라서 사용자가 정해주는 값인데 이걸 정해주는 것도 좀 스트레스입니다.
그래서 2015년에는 PReLU 활성화 함수가 제시되었고, 이는 곱해지는 작은 양수 값을 학습의 대상으로 보는 방법입니다.
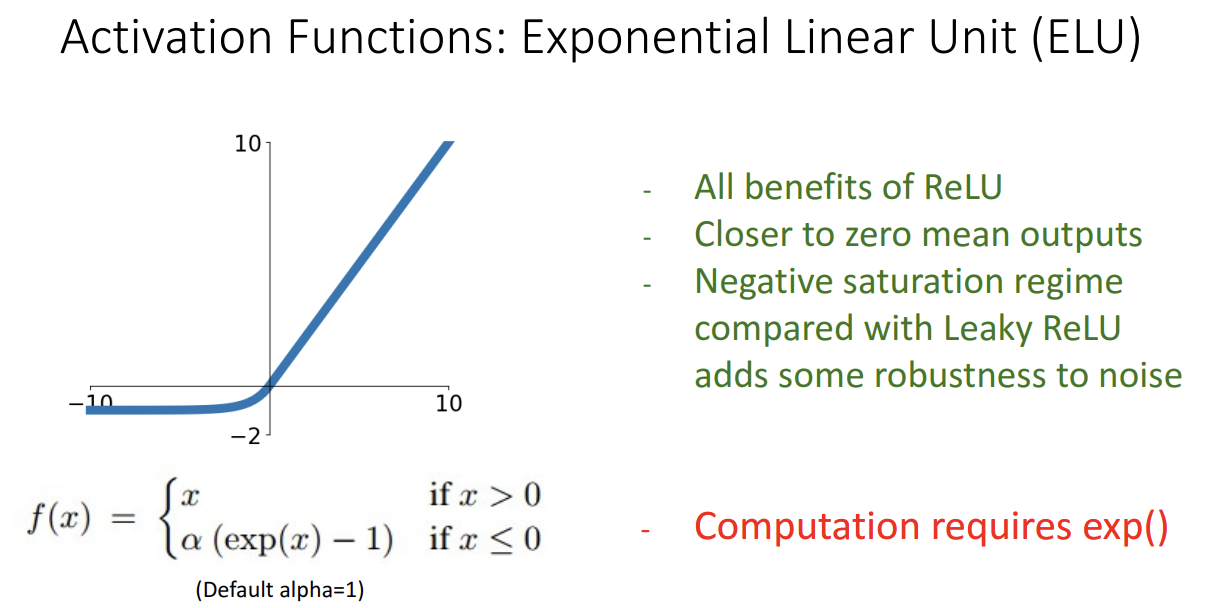
다음으로는 ReLU 함수를 조금 더 보완한 ELU 입니다.
해당 활성화 함수가 나오게된 이유는 ReLU의 경우 input 값이 0 쪽일 때는 미분이 불가능하다는 문제가 있었기 때문입니다.
ELU는 ReLU를 smooth 시켜서 해당 문제점을 극복했습니다.
이렇게 하면 ReLU의 장점들은 모두 챙기고 noise에도 더 Robust해진다는 장점이 있습니다.
물론 단점도 있습니다.
Exponential 함수는 계산이 복잡합니다.

마지막으로 살펴볼 활성화 함수는 SELU 입니다.
ELU의 Scaled 버전으로 생각해주시면 되겠습니다.
SELU는 ELU와 유사하지만 곱해지는 파라미터 값을 수학적으로 규정해놨습니다.
위에 보이는 복잡한 해당 숫자들을 사용한다면 Self-Normalizing 되어서 BatchNorm이 필요가 없어지게 된답니다.
저 숫자들이 뭐길래 그게 되지? 라는 의문점이 들면 논문을 찾아서 읽어보면 된다는데 무려
증명 파트 Appendix가 91장이나 된답니다. 저는 못 읽겠네요..ㅎㅎ
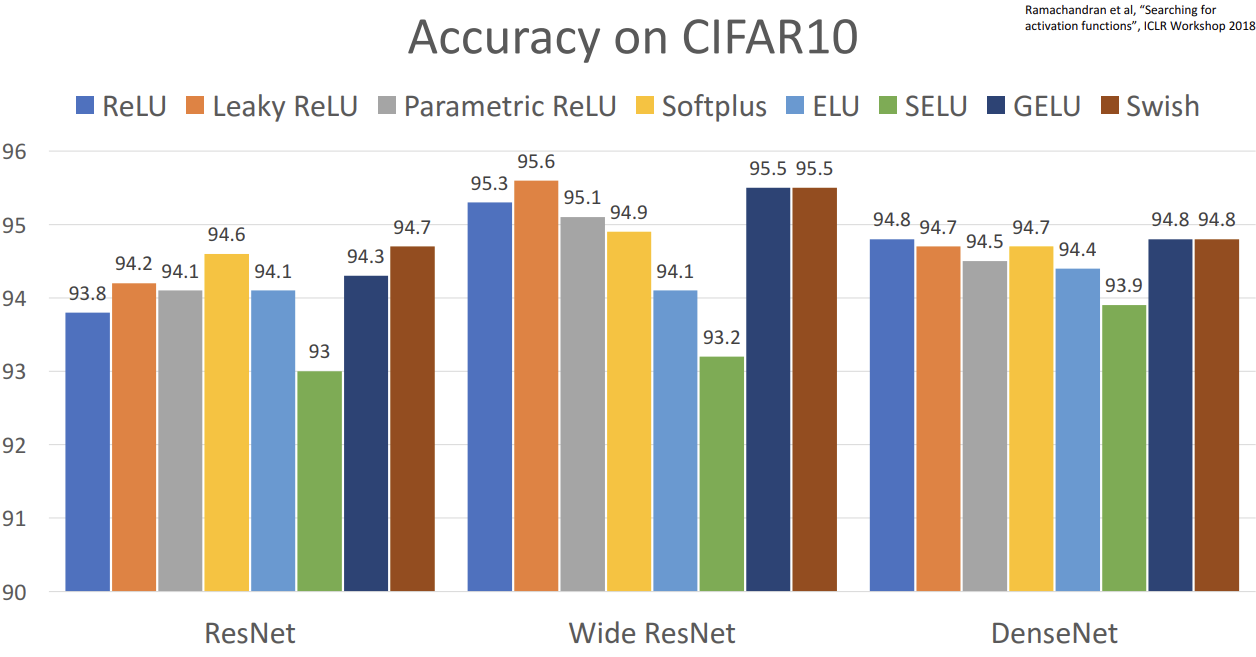
각 활성화 함수들을 모델에 사용했을 때의 성능을 비교해놓은 논문도 있습니다.
엎치락뒤치락 조금씩 차이가 있어보이기는 하지만, 사실 퍼센티지만 따지면 그렇게 큰 성능 차이는 없습니다.

교수님께서는 어렵게 생각할 필요없다. 그냥 ReLU 써라 라고 조언해주십니다.
성능을 0.1% 까지 짜내고 싶으면 변형본들 써라.
하지만 시그모이드/tanh 는 절대 중간에 넣는거 아니다.
네트워크가 수렴하지 못하기 때문입니다.
Data Preprocessing
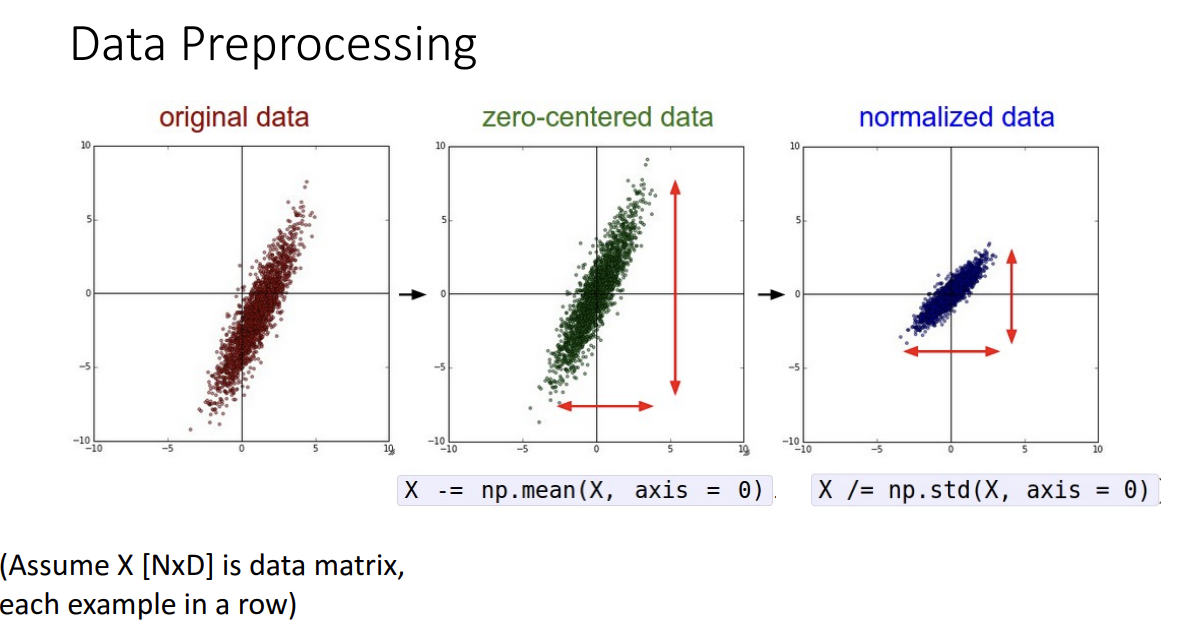
다음은 데이터 전처리입니다.
해당 개념은 사실 새로운 개념은 아니고 데이터 분석을 해본 사람들이면 한번씩 해보았을 내용입니다.
효율적인 학습을 위해서 원본 데이터를 zero-centered 시키고 정규화시키는 그러한 내용입니다.

Zero-centered 시키는게 왜 중요한지는 앞서서 시그모이드 함수가 zero-centered 되지 못해서 생겼던 문제점들을 다시 떠올려보면 됩니다.
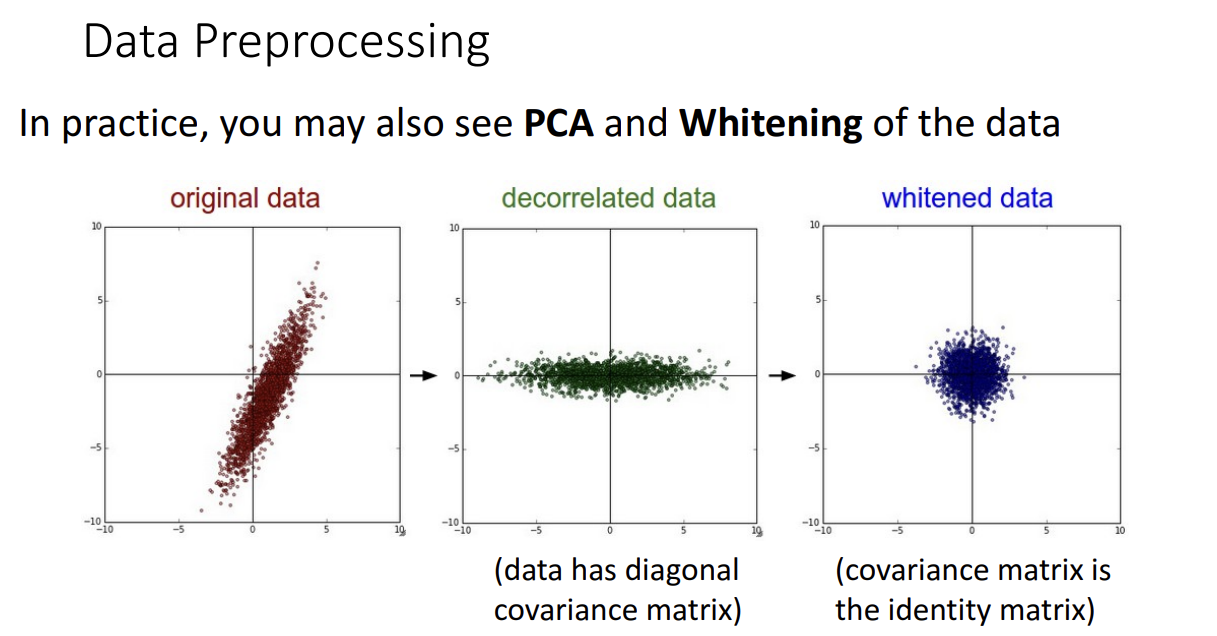
다른 전처리 방법으로는 PCA를 통해 Decorrelated 시키는 방법도 있습니다.
원본 데이터셋을 rotate 시키는 방식으로 이해하시면 되는데 축끼리 uncorrelated 될 수 있도록 즉 데이터가 diagonal covariance 행렬을 가질 수 있도록 하는 겁니다.
Whitening 시키는 전처리 방법도 있는데 사실 PCA도 그렇고 whitening도 그렇고 이미지에서 잘 사용 안한다고 합니다.

이미지에서 데이터전처리가 이뤄진 사례를 보면
AlexNet에서 mean image를 빼준 경우, 이 경우는 32x32x3 각 픽셀별 mean 값을 빼줬습니다.
VGGNet의 경우 channel별 평균 이미지를 빼줘서 총 3개의 이미지를 빼줬습니다.
ResNet의 경우 VGGNet의 경우에서 더 나아가 채널별 표준편차로 나눠주는 정규화 과정도 거쳤습니다.
Weight Initialization
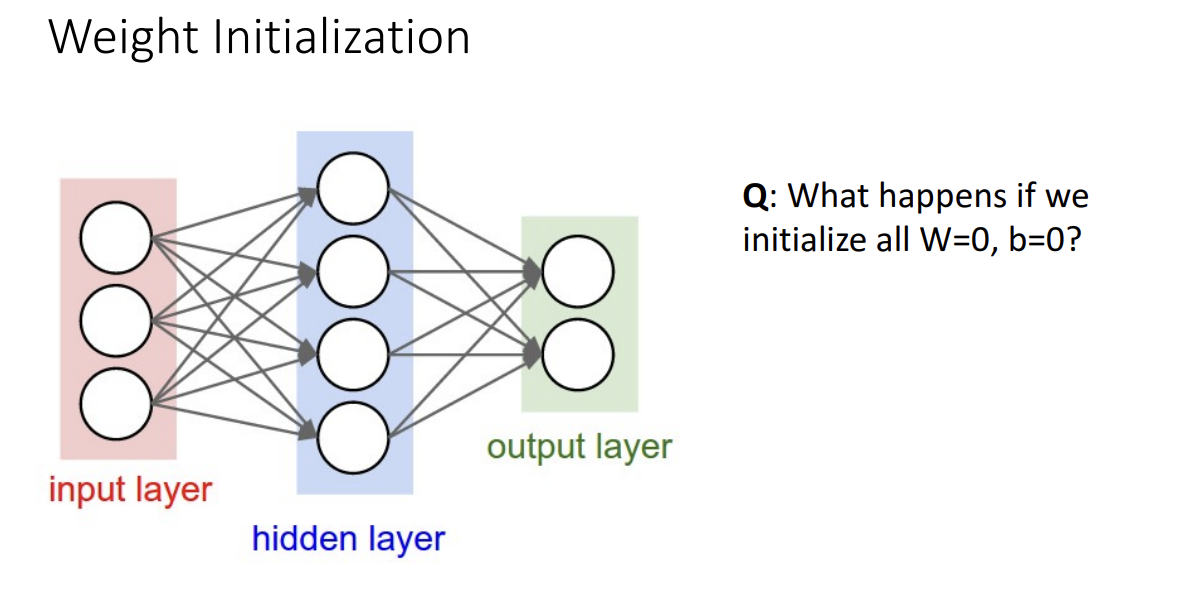
다음으로 가중치 초기화 방법입니다.
가중치를 학습시키기 앞서서 일단은 어떤 값으로 시작할지를 정해야합니다.
근데 그저 가중치랑 편향을 0으로 두고 시작해도 될까요?
그렇게 두는 것은 상관없지만 결과는 안 좋을 것입니다.
왜냐면 모든 Output이 0이 되어서 gradient가 늘 똑같게 되어서 학습이 전혀 안 이루어지게 되기 때문입니다.

그래서 나오게된 다음 아이디어는 아주 작은 랜덤한 값으로 초기화 시켜서 시작하는 방식입니다.
이 경우는 shallow한 네트워크에는 적합하지만 deep한 네트워크에는 부적합합니다.
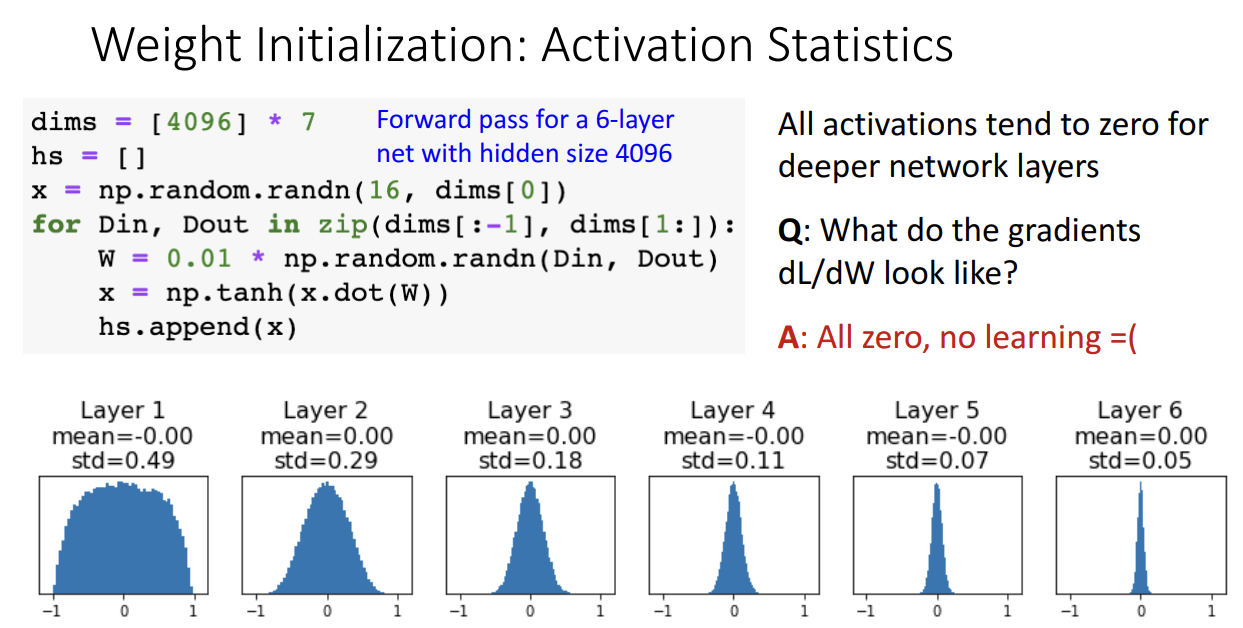
위 예시를 보시면 이해가 될겁니다.
6개 hidden layer를 가진 네트워크를 구성해보고 가중치를 항상 아주 작은 랜덤 값으로 초기화해서 학습을 진행한 결과입니다.
이 경우 층을 거칠수록 gradient 값이 점점 0에 가깝게만 산출되기 때문에 학습이 전혀 이뤄지지 않게됩니다.
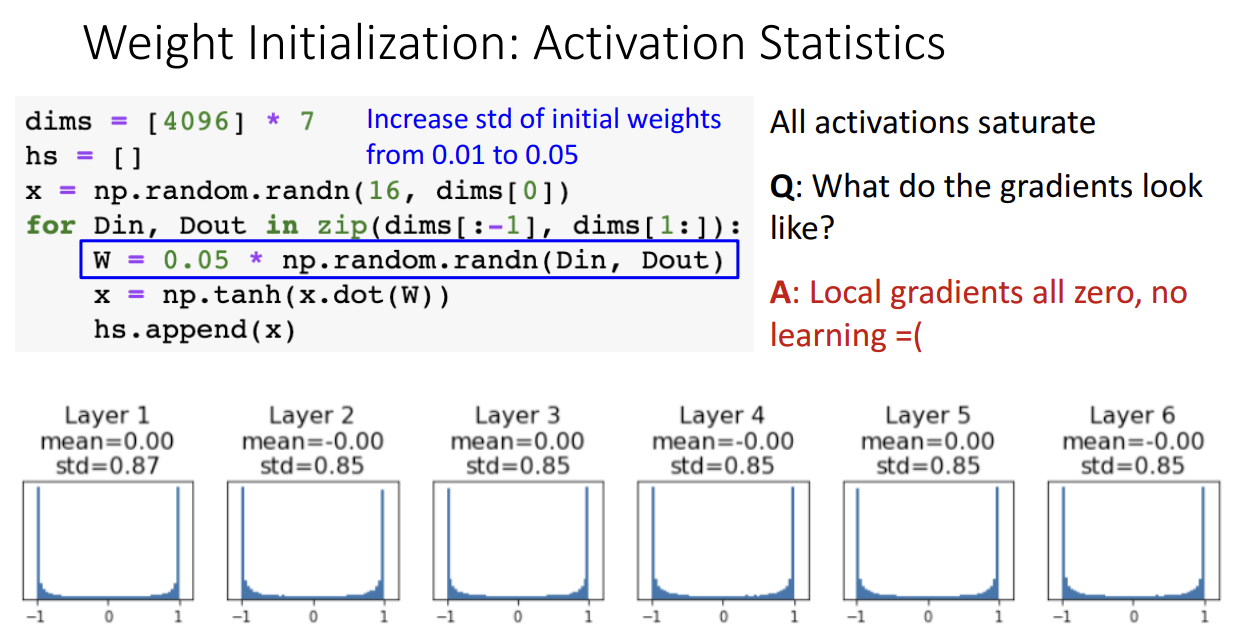
혹시 0.01을 곱한값이 너무 작아서 그런건가 싶은 생각에 0.05로 조금 늘려서 랜덤한 값으로 초기화해본 결과입니다.
이 경우도 Local gradient가 항상 0이 되어서 학습이 잘 안되는 결과를 얻어낼 수 있었습니다.
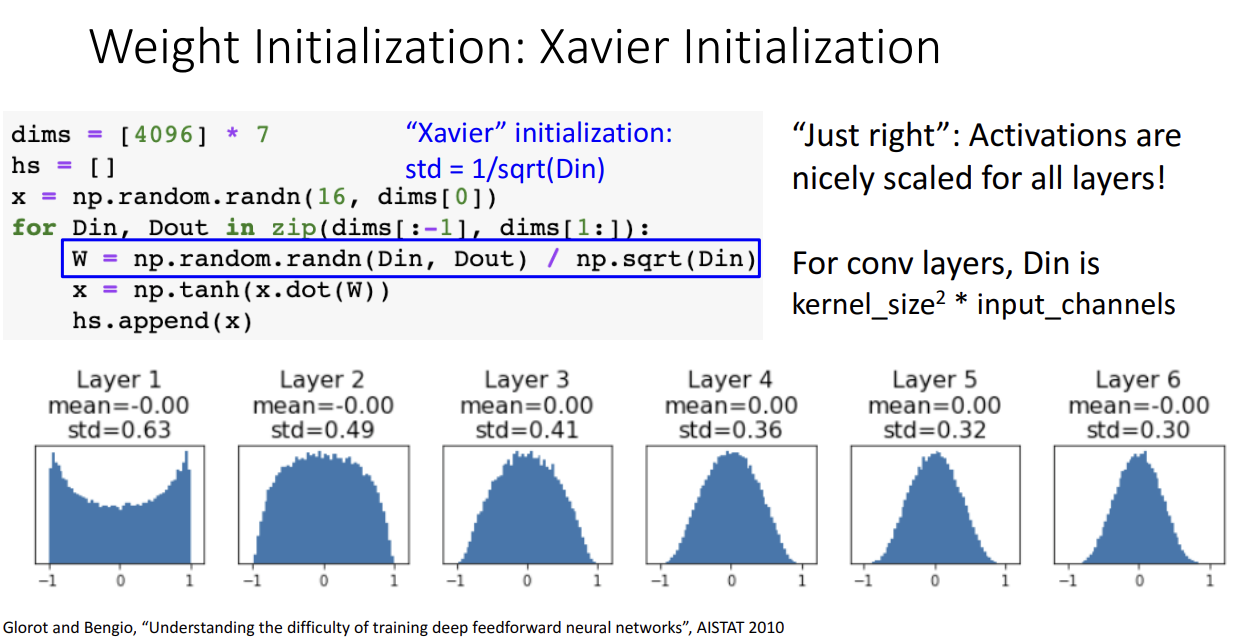
그래서 나온 다음 초기화 방법은 바로 요슈아 벤지오 교수님의 제자인 자비에 박사님의 자비에 초기화 입니다.
해당 초기화를 사용하면 모든 층에서 gradient가 적절하게 계산되어 학습이 잘 이루어지는 것을 알 수 있습니다.
초기화 식은 상당히 간단해보이는데요. 해당 식이 나온 이유는 다음과 같습니다.

Output의 분산을 Input의 분산과 동일하게 만들고 싶은게 자비에 초기화 아이디어의 시작입니다.
W와 x가 independent 하다는 가정하에 로 만들기 위해서
되어야만 하다는 식이 도출되고 이를 초기화 값으로 사용한 것입니다.

자비에 초기화가 좋다고 해서 모든 경우에 적용되는 말은 아닙니다.
앞서서는 tanh 활성화 함수를 사용한 경우였는데, 사실 자비에 초기화는 zero-centered된 활성화 함수에 적용하는 걸 전제합니다.
따라서 ReLU 함수에 자비에 초기화를 쓰면 위 그림처럼 다시 gradient가 0으로 수렴하게 되어서 학습이 이루어지지 않게 됩니다.
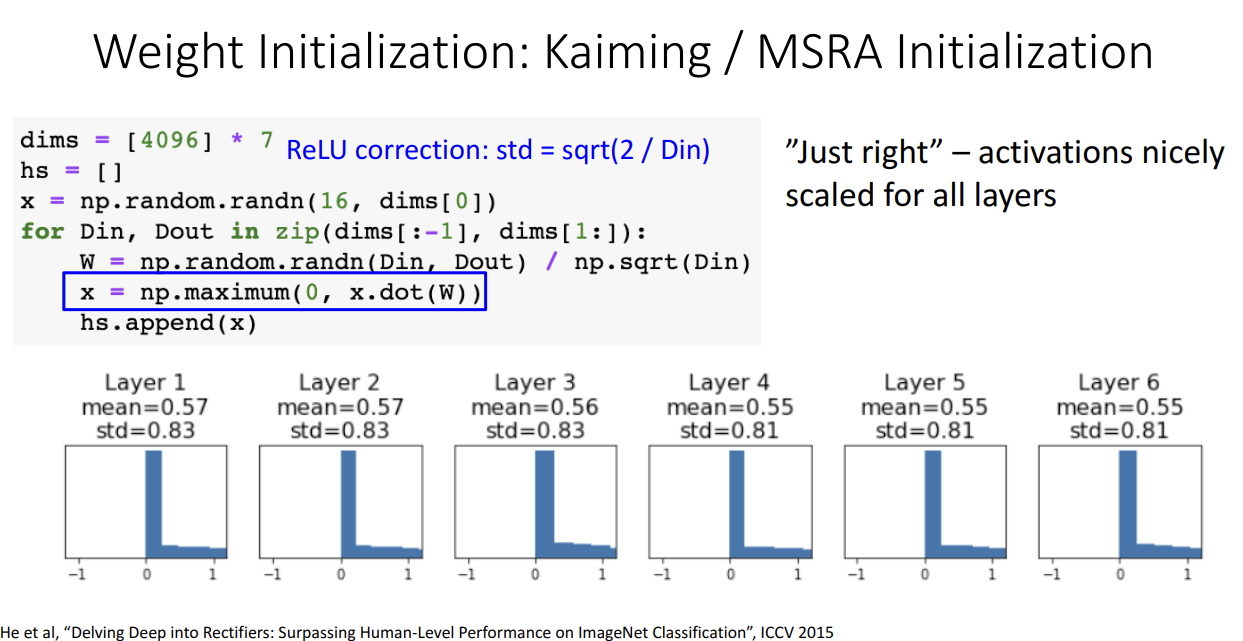
ReLU 활성화 함수에 적합한 초기화 방법은 따로 있습니다.
무려 ResNet을 만드신 Kaiming He 박사님의 Kaiming 초기화 혹은 He 초기화 혹은 MSRA 초기화 방법입니다.
위 그림을 보시면 모든 층에 일정하게 gradient가 계산되어서 학습이 잘 이루어진다는 것을 알 수 있습니다.

ResNet에서 He 초깃값을 사용해서 학습할 때 한 가지 문제점이 발생했습니다.
He 초깃값은 가 되도록 동작하는데 ResNet은 Additive Shortcut을 더해서 출력값을 보내기 때문에 gradient가 exploding 하는 문제가 생깁니다.
이에 대한 해결책으로는 첫번째 Conv를 초기화할 때 He 초깃값 사용하고, 두번째 Conv를 초기화할 때는 0으로 초기화 하면 가 된다고 합니다.
Regularization
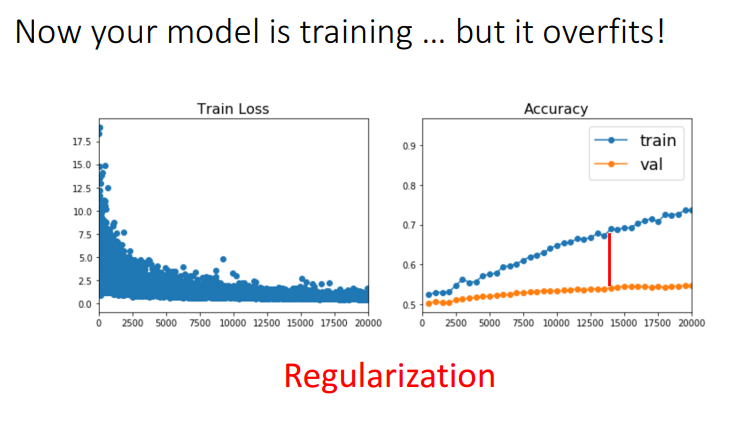
앞선 학습 기술들을 다 사용하면 이제 학습이 얼추 됩니다.
하지만 한 가지 문제점을 더 해결한다면 금상첨화입니다.
바로 모델이 Overfitting되는 문제입니다.
이 경우에는 이전 강의에서도 잠깐 나왔던 Regularization 기법으로 해결 가능합니다.

Regularization 기법으로 이전 영상에서 나왔던 것은 Loss 에 Regularization term을 추가해주는 것입니다.
대표적인 Regularization term으로는 L2, L1 regularization term이 있습니다.
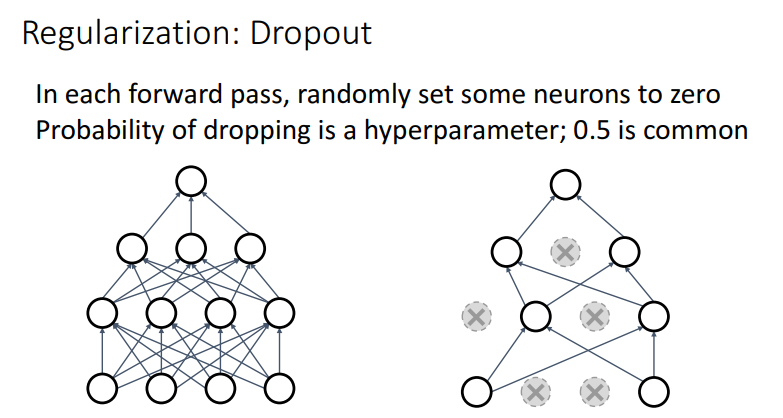
Loss 함수에 직접적으로 규제를 걸어주는 방식 대신에,
네트워크의 뉴런을 끊어버리는 방식으로 규제를 걸어줄 수도 있습니다.
특정 확률에 따라 뉴런을 끊어버리는 방식인 Dropout인데 일반적으로 0.5를 많이 사용하곤 합니다.
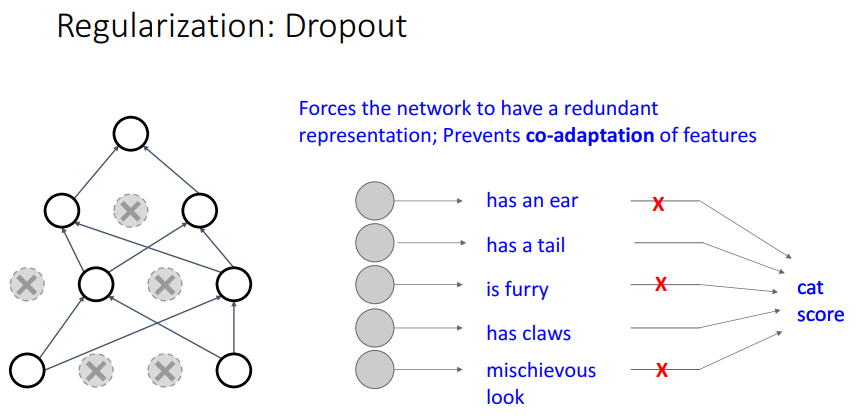
Dropout이 왜 좋은지 설명하는 방식 중에 위 같은 그림을 사례로 설명하는 방식이 있습니다.
왜 강제적으로 뉴런을 끊는게 좋냐면은 뉴런은 분류 Task를 수행하는데 있어서 꼭 필요한 정보들만을 담고 있지는 않기 때문입니다.
예를 들어 고양이로 분류하기 위해서 꼬리, 발톱과 같은 정보는 중요하지만, 귀가 있다, 털이 있다 이런건 크게 중요하지 않을 수 있습니다.
이렇게 다른 클래스 이미지와 중복되는 표현은 제거해서 모델의 성능을 높일 수 있습니다.
그 외에도 Dropout은 어떤 뉴런을 끊을지에 따라서 다른 모델이 됩니다.
따라서 학습을 여러번 진행할 때마다 끊기는 뉴런이 다르고 해당 경우들을 종합해서 학습하는 방법은
결국 앙상블 효과를 가져올 수 있습니다.

일반적으로 네트워크에 Dropout을 사용하는 것은 Overfitting을 방지하여 학습을 잘하기 위함입니다.
따라서 Test 시에는 Dropout을 구조에서 빼버려서 랜덤한 결과보다는 Deterministic 한 결과를 얻도록 합니다.

코드로 표현하면 위와 같습니다!
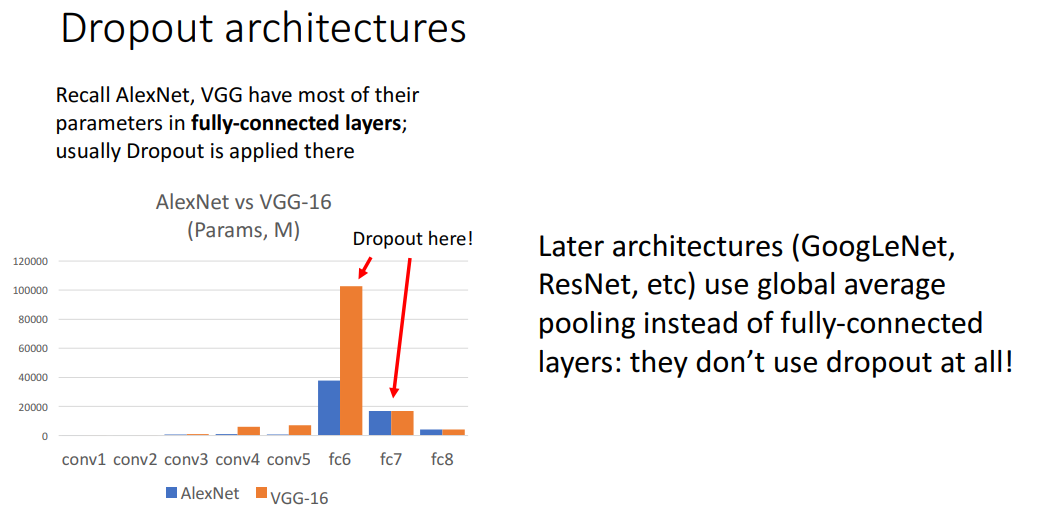
Dropout은 깊은 구조의 네트워크에서 Overfitting을 줄이기 위해서 필수이긴 하지만,
GoogLeNet이나 ResNet의 경우 global average pooling을 FC Layer 대신 사용하기 때문에 굳이 dropout을 사용하지 않는다곤 합니다.

결론적으로 말하자면 large deep neural network 학습에 도움을 주기 위해서 L2 norm을 Loss에 추가하거나 Batch Normalization을 사용하는게 더 일반적이라고 합니다.
마지막으로 해당 강의가 컴퓨터 비전 강의이기 때문에, Regularization 방법으로 Augmentation도 다룹니다.



위 그림처럼 뒤집고, 자르고, 색상 바꾸고 여러가지 방식으로 데이터 증강을 하는 것도,
모델이 너무 특정 데이터셋에만 맞춰서 학습되는 현상을 방지해줄 수 있습니다.
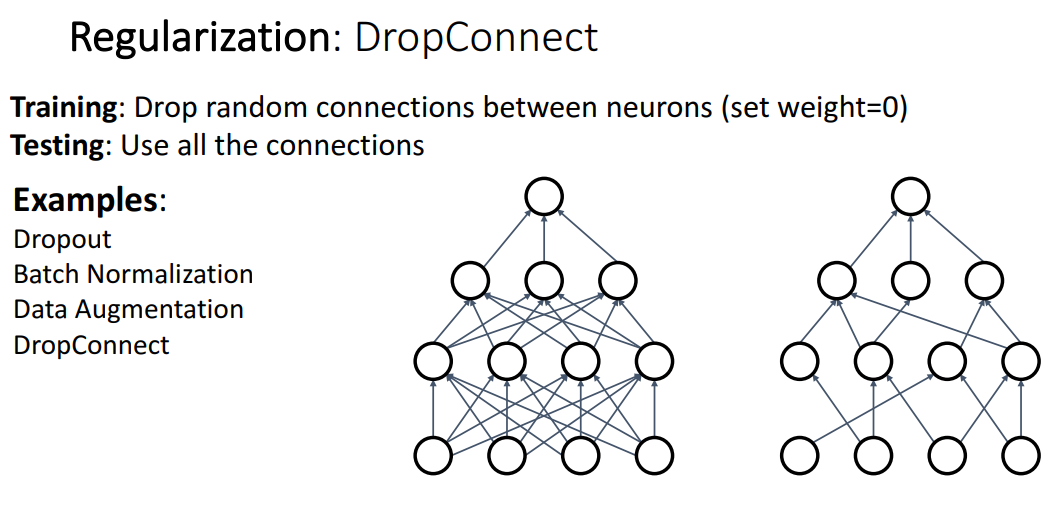
Dropout과 유사하지만 뉴런을 지우는 것이 아니라 뉴런간의 연결을 0으로 두어서 연결을 끊는 방식.

ResNet 블록에서 특정 블록을 지우는 방식.

이미지를 Cutout 해서 일부 이미지는 날려버린 상태로 학습하는 방식.

하나의 클래스만을 예측하는게 아니라, 두개 이상의 클래스 이미지를 합친 상태로 학습하여
합쳐진 이미지의 비율을 예측하는 방식.

여러가지 방식의 Regularization이 소개되었는데 위에 검정글씨로 쓰여진 방법들이 주로 쓰인다고 합니다.
