
본 게시물은 고려대학교 스마트생산시스템 연구실 2023년 동계 신입생 세미나 활동입니다.
Michigan 대학의 Justin Johnson 교수님의 강의를 공부하는 형식입니다.
관련 유튜브 영상은 여기에서 확인 가능합니다.
Lecture 5: Neural Networks 강의에서는 배울 수 있는 내용은 다음과 같습니다.
- Feature Transforms
- Neural Networks
- Activation Functions
- Comparison to Human Brain
- Space Warping
- Universal Approximation
- Convex Functions
Feature Transforms

앞서 Linear Classifiers에 대해 배울 때 한 가지 문제점이 존재했습니다.
위 그림과 같은 경우 Linear하게 Seperate 시킬 수 없으며,
클래스별로 하나의 template만을 학습할 수 있어서 different한 modes는 동시에 학습이 불가능하다는 점입니다.
이러한 경우 Linear Classifiers는 제대로 작동하지 못합니다.
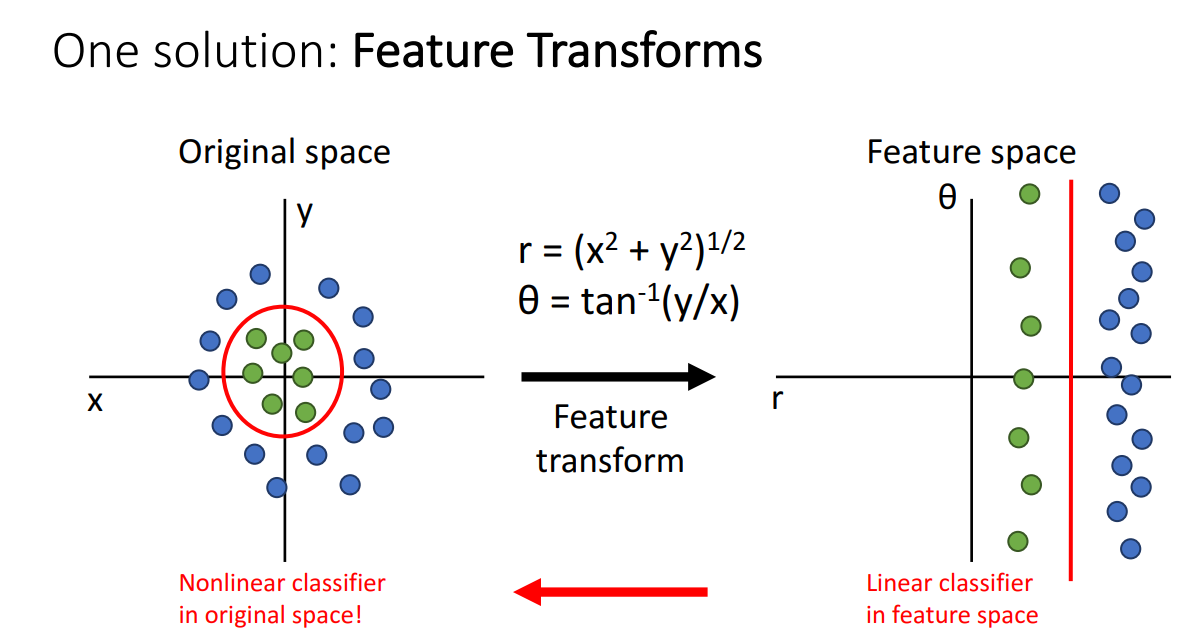
이를 극복하고자 나온 방법이 Feature Transforms 입니다.
위 그림을 예시로 설명을 드리자면 왼쪽 Original space 상에서는 두 클래스를 선형적으로 구분할 수 없습니다. 따라서 Feature를 오른쪽과 같이 변형을 시켜서 타점한 뒤, 두 클래스를 선형적으로 나눌 수 있는 Classifier를 학습시키고 다시 왼쪽으로 Feature transform 시켜 Nonlinear Classifier로 사용하는 방법입니다.
해당 방법이 일반적인 Feature Transform이라면 이미지에 특화된 Feature Transform도 존재합니다.
Color Histogram
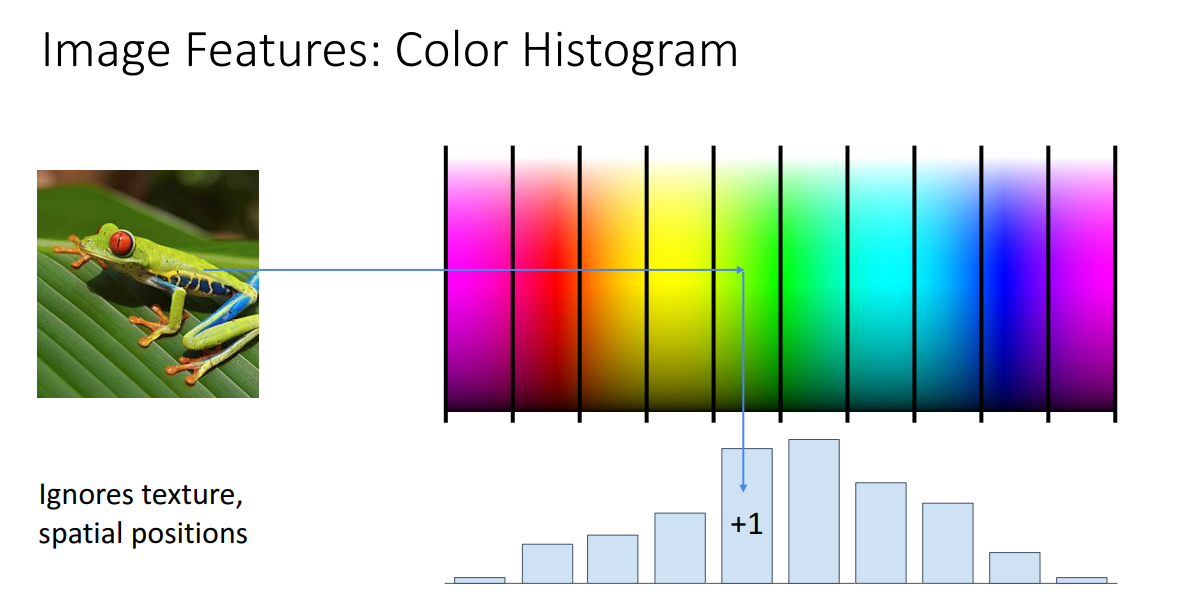
첫번째는 Color Histogram 입니다.
해당 방법은 이미지의 Feature Representation을 잘 학습하기 위해서 변형을 시키는 방법인데요,
Texture, spatial position 과 같은 정보는 무시하고 오직 색상만을 오른쪽 Color map bin들에 타점하여 Histogram을 산출하는 방법입니다.
Histogram of Oriented Gradients (HoG)

두번째는 Histogram of Oriented Gradients (HoG)입니다.
해당 방법은 Color Histogram과 반대로 이번에는 색상만 날리는 변형 방법입니다.
HoG 변형을 하게 되면, edges의 local orientations과 local strength를 학습할 수 있게 됩니다.
즉 위 그림의 예시를 보시면 노란 박스와 같이 edge가 약한 배경부분은 변형을 거쳤을 때 아무런 모양이 나오지 않지만, 빨간 박스와 같이 edge가 포함된 부분은 변형을 거쳤을 때 방향성이 있는 선으로 표현됩니다. 마지막으로 파란색 박스와 같이 모든 방향으로 edge가 있는 경우는 변형을 거쳤을 때 퍼져있는 모습을 보여줍니다.
해당 방법론은 texture와 position을 포착할 수 있고 small 이미지 변환에 robust하다는 장점이 있습니다.
따라서 Object Detection 분야에서 자주 연구되곤 합니다.
Bag of Words
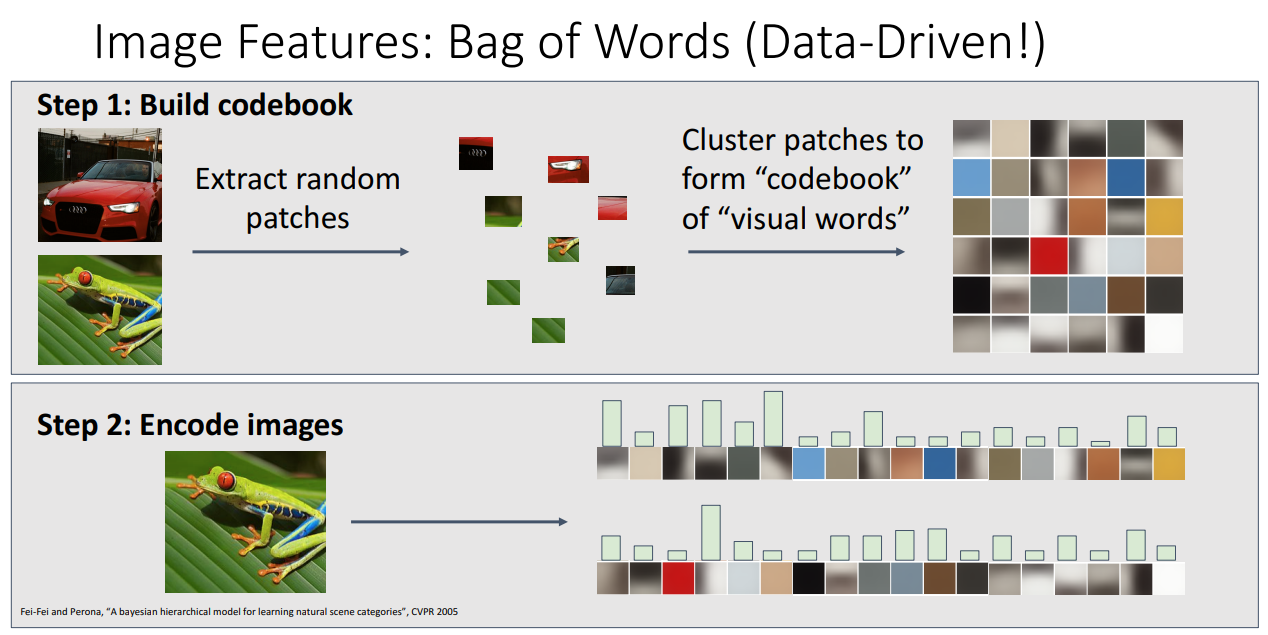
세 번째는 Bag of Words 입니다.
해당 방법론은 Data-Driven 방법이며, 이미지로부터 랜덤한 패치를 추출하고,
해당 패치들을 클러스터링하여 codebook을 만듭어냅니다.
그리고 나서 이미지를 해당 codebook에 상응하도록 인코딩시키는 방식으로 feature를 변형시킵니다.
앞서 살펴본 3가지 방법론을 각각 사용하기도 하지만 합쳐서 사용하는 방법도 존재합니다.
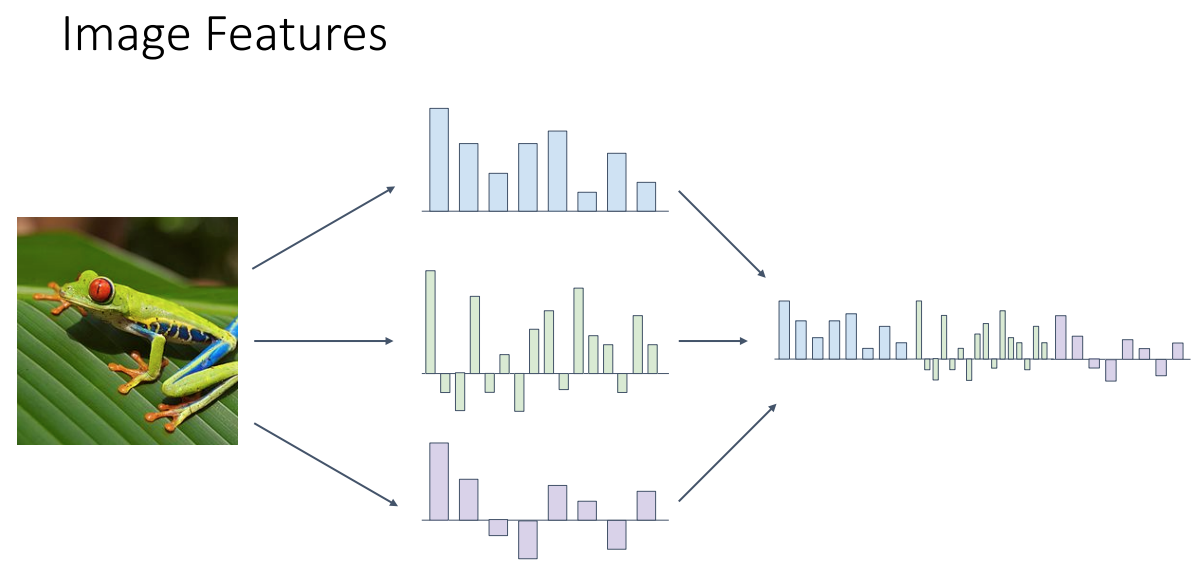
위 그림과 같이 Color Histogram, HoG, Bag of Words로 이미지를 변형시키고 이를 이어붙여서 long high-dimensional feature vector를 만들어낼 수 있습니다.
지금까지 Lienar Classifier가 가지고 있던 문제를 해결하기 위한 방법으로 Feature Transformations 방법론들을 살펴봤는데요, 사실 해당 문제를 해결하기 위한 방법으로 더욱 주목받고 현재까지 활발하게 연구가 되고 있는 방법은 바로 Neural Networks 입니다.
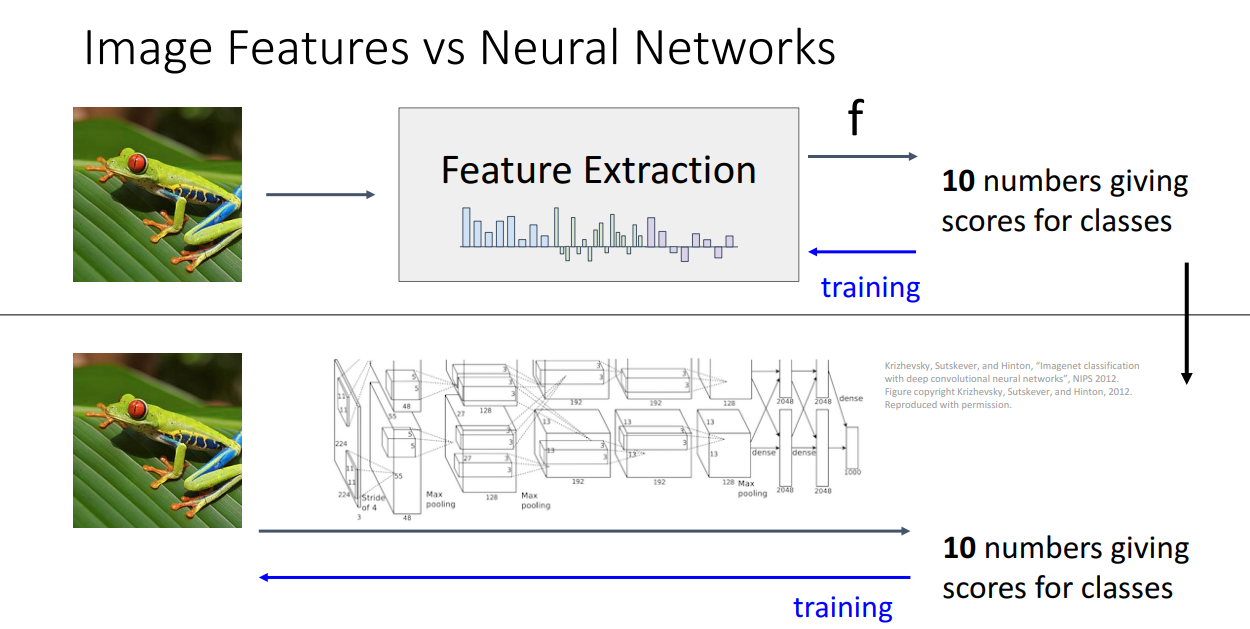
자세하게 살펴보기 전에 간단하게 Feature Transformation 방법과 Neural Networks가 어떻게 다른지 비교해보겠습니다.
전자의 경우 학습의 대상이 class score를 산출하는 예측 과정 뿐입니다.
따라서 Feature를 변형시키는 부분은 Rule-based로 진행하고 학습은 오직 예측 과정만 진행하게 됩니다.
하지만 Neural Networks는 Feature를 추출 및 변형하고 이를 통해 예측을 하는 모든 과정이 학습의 대상이 됩니다. 즉 Feature Extraction과 Linear Classifier 모두를 학습하는 과정입니다.
Neural Networks
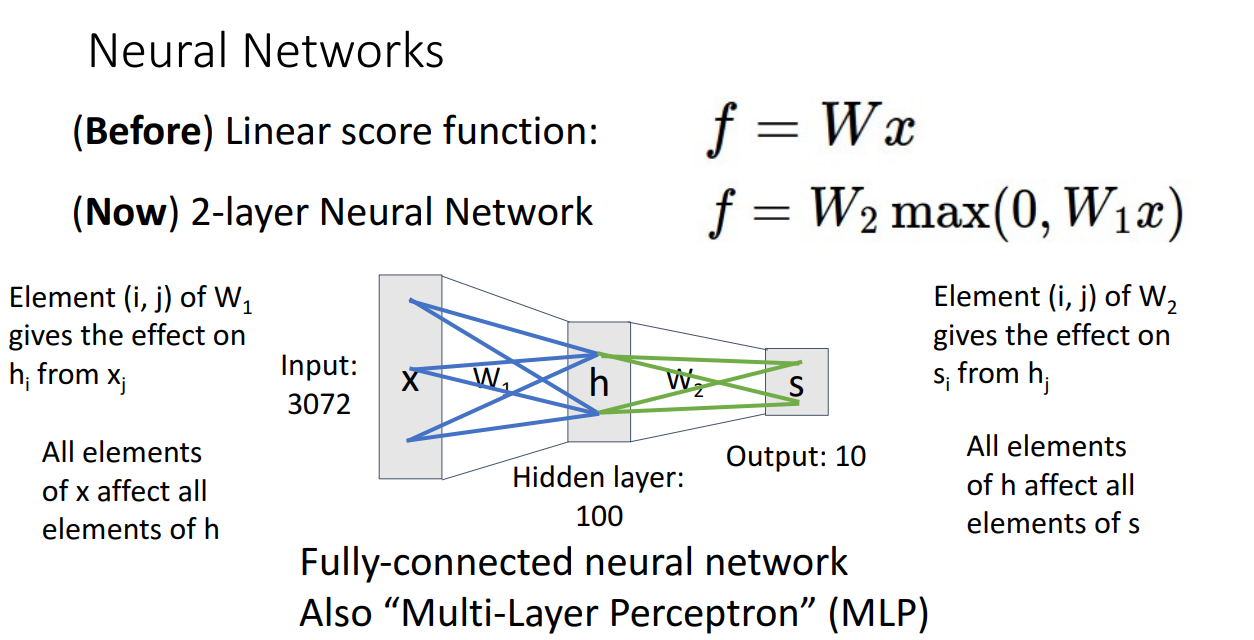
Neural Networks는 learnable weight matrices 가 여러개입니다.
Weight Matrices의 개수에 따라 2-layer인지 3-layer인지 결정되는 식입니다.
여러개의 Weight 행렬을 사용함으로써 Non-linear한 분류도 가능하게 합니다.
위와 같이 Input vector, Hidden weight matrix, Output vector의 element들이 모두 연결되어 학습이 진행되는 경우 Fully-connected neural network 혹은 Multi-Layer Perceptron (MLP)라고 불립니다.
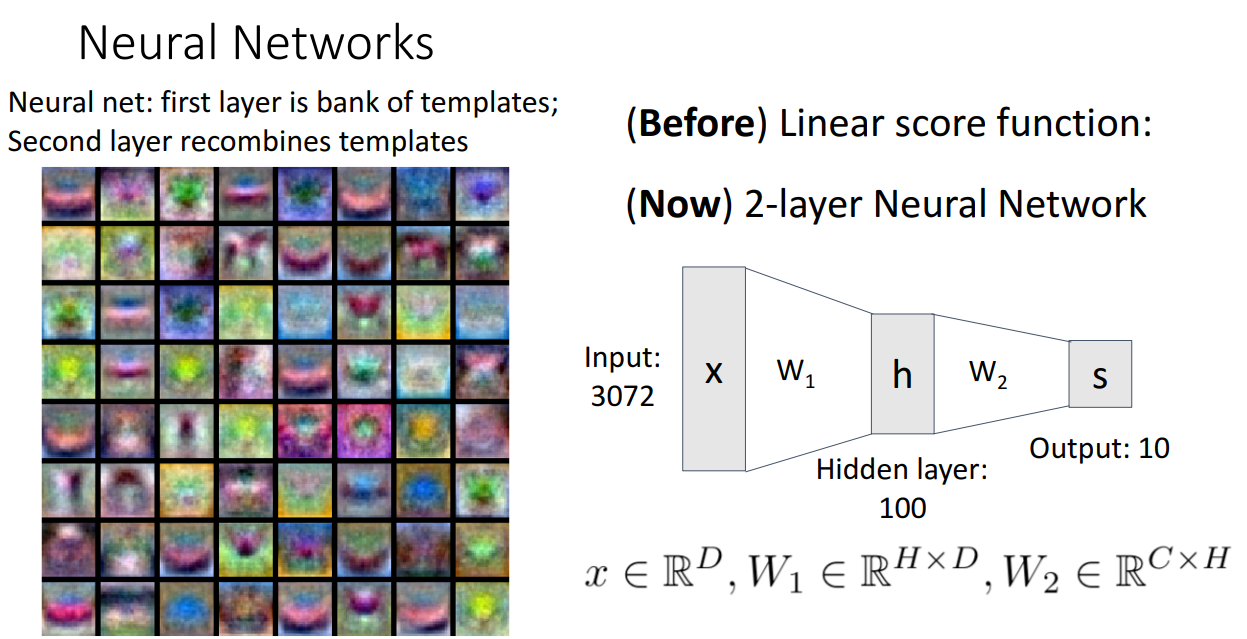
이렇게 여러층을 쌓아서 네트워크 구조로 모델을 구성하면 위와 같은 장점이 있습니다.
바로 각 class 별로 여러개의 template을 통해 score를 산출할 수 있습니다.
즉 multiple mode를 학습할 수 있습니다.
3장에서 제시되었던 two-headed horse problem도 극복이 가능합니다.
여러개의 층 중에 초반에 있는 층들은 not interpretable하기 때문에 사람이 직접 구별하기는 어렵습니다.
하지만 후반으로 갈 수록 더욱 세부 정보를 학습할 수 있도록 template이 생성됩니다.
위 그림을 보시면 template이 repeated 되는 경향이 있는데 이는 분류 성능을 높이기 위해 Neural Network 이 학습을 통해 선택한 결과입니다.
Redundancy 에 대한 의문이 있을 수는 있지만 뒤로 갈 수록 Prune Out(가지치기)하기 때문에 괜찮습니다.
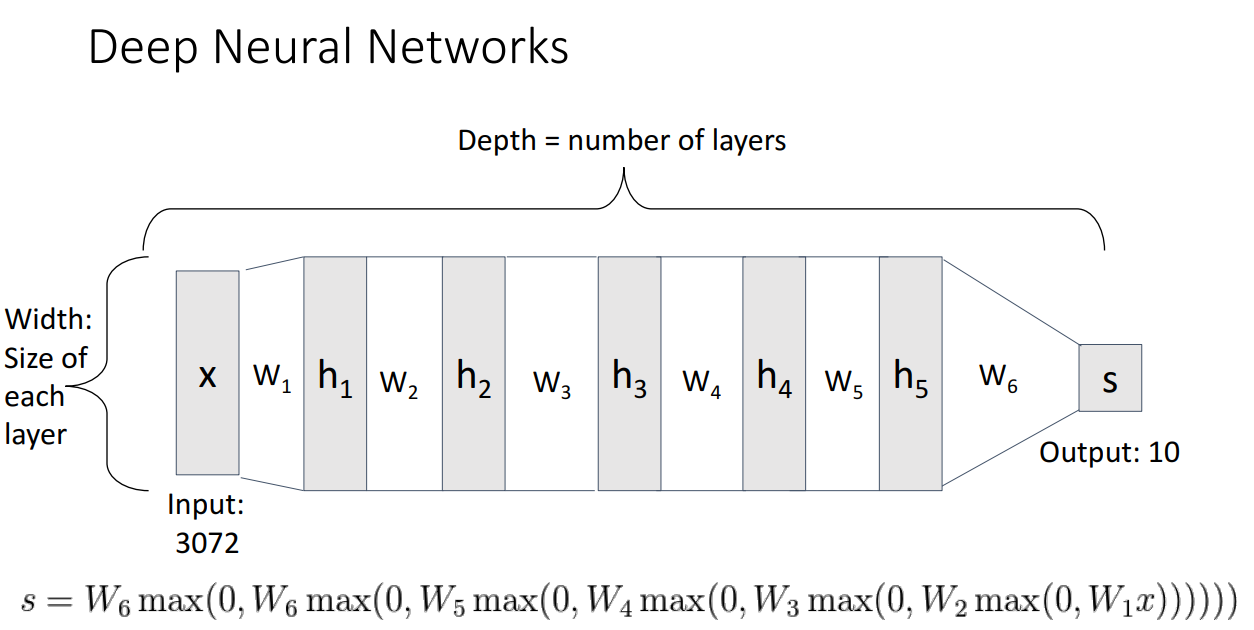
훨씬 Deep하게 쌓는 것도 가능합니다.
Activation Functions

앞서 Neural Networks를 설명드릴 때 보시면, max term이 붙어있는 것을 보실 수 있습니다.
이를 구체적으로 설명드리면 Rectified Linear Unit 함수 즉 ReLU 함수입니다.
ReLU 함수는 양수 값일때는 Wx 값을 음수 값일 때는 0 값을 산출해내는 비선형함수입니다.
이와 같이 activation function (활성화 함수)을 사용하는 이유는 이를 사용하지 않고 Weight 행렬만 연달아서 곱해버리면 사실 상 Nonlinearity를 표현할 수 없고 선형적으로밖에 분류할 수 없기 때문입니다.

ReLU 함수 외에도 여러 활성화함수들이 있습니다.
이진분류를 위한 Sigmoid, ReLU 함수의 문제점인 Gradient Vanishing 을 보완하는 Leaky ReLU 혹은 ELU 함수들도 존재합니다.
일반적으로는 ReLU가 디폴트로 사용하기에 좋은 활성화함수 입니다.
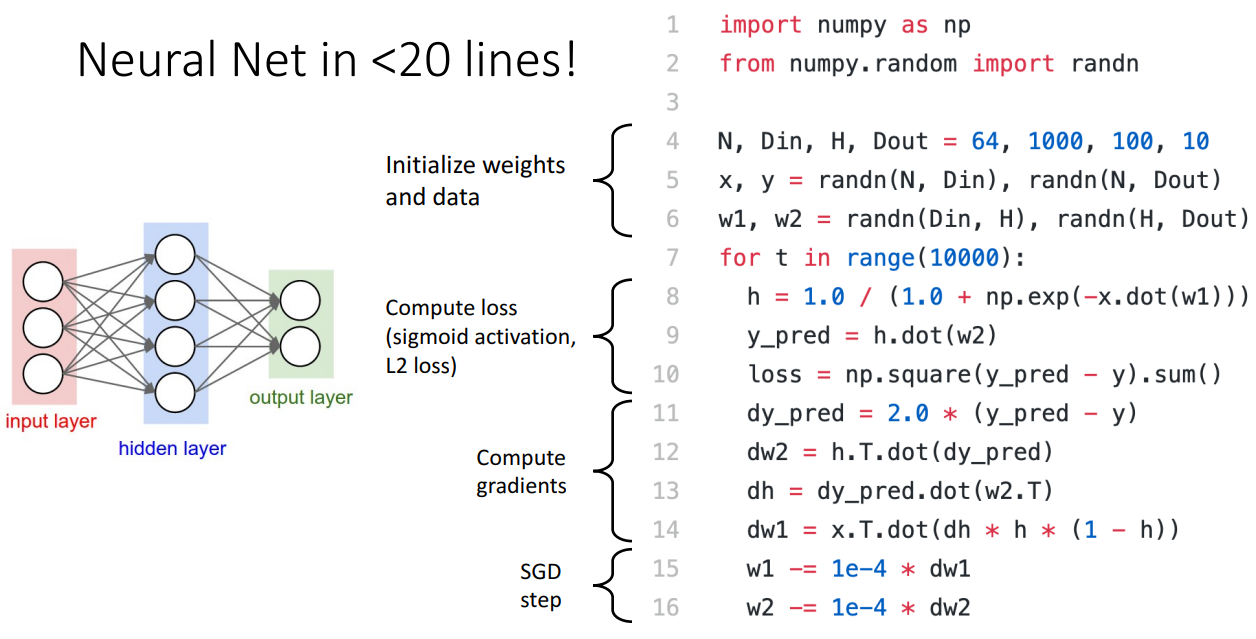
Neural Networks의 장점은 구현이 쉽다는 것입니다.
20줄 안으로 구현하는 모습을 볼 수 있습니다.
Comparison to Human Brain
교수님은 Neural Network가 사람의 뇌와 많은 점에서 유사하다고 하십니다.
그래서 Neuron을 뜻하는 Neural 단어가 쓰이는 것이겠지요.
뇌공학자는 아니시니 간단하게만 설명해주십니다.
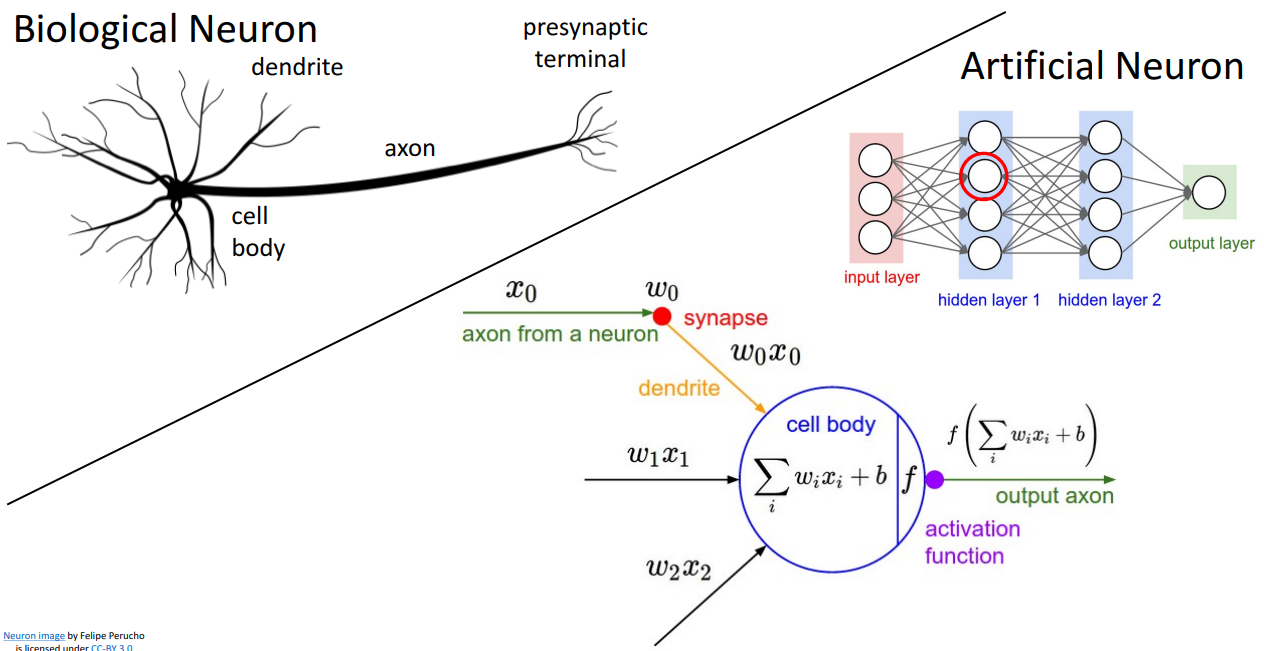
위 장표는 둘의 Similarity, 아래 장표는 둘의 Dissimilarity 입니다.
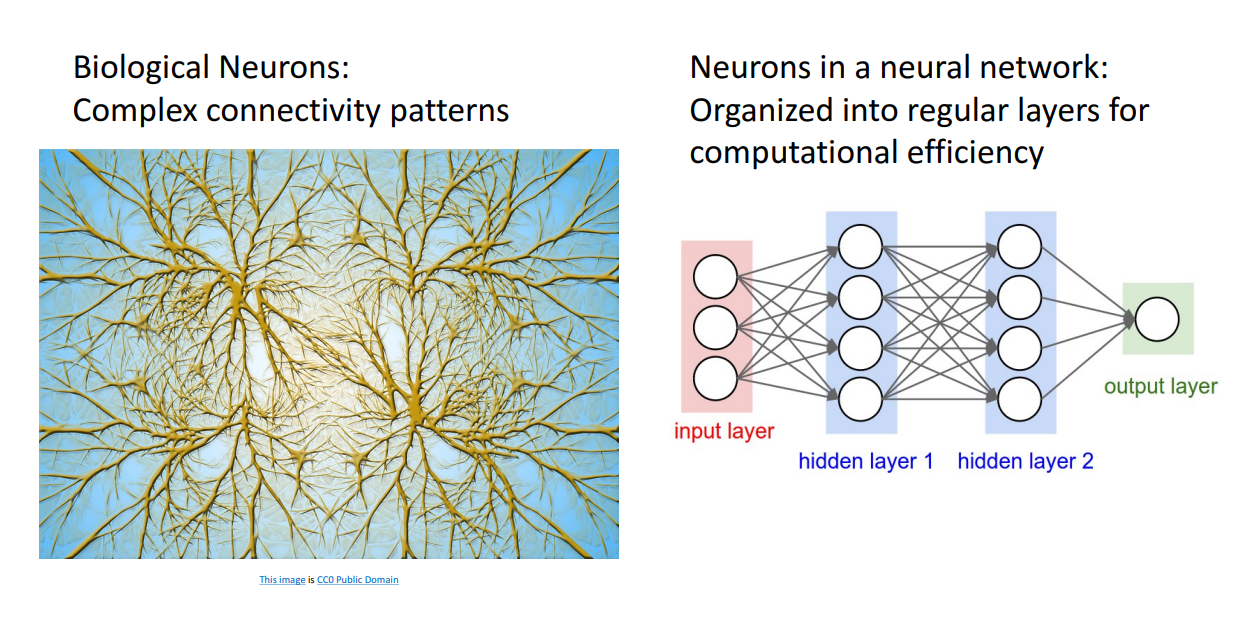
차이는 Neural Network는 Regular 하게 구조화되어있다는 점, 사람의 뇌는 더 복잡하게 연결되어있다는 점입니다.
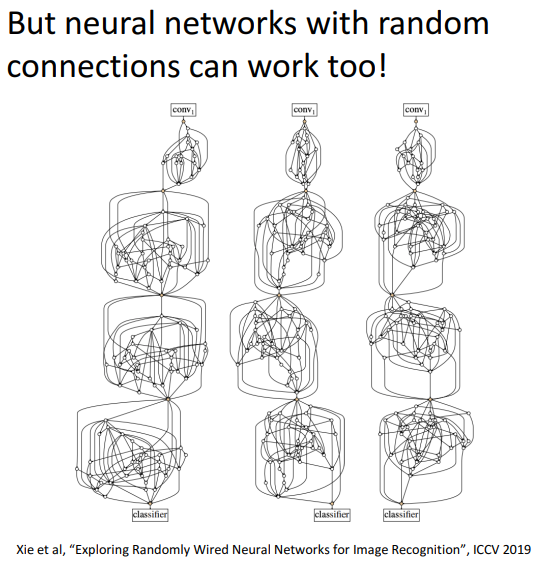
따라서 사람의 뇌처럼 신경망을 구성하고자하는 연구도 있었습니다.
Space Warping
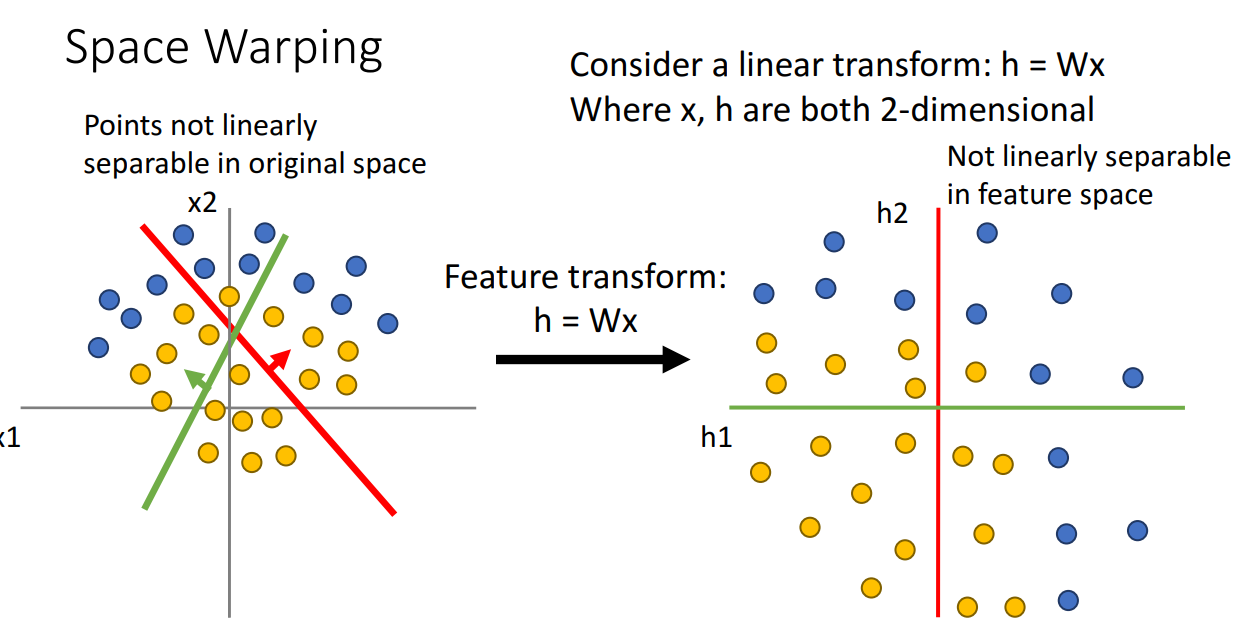
데이터들이 Linear Classifier로 분류가 되지 않는 상황은 분명 존재합니다.
이 때 위와 같이 Feature transform을 통해 다른 좌표축으로 타점할 수 있습니다.
이 경우에도 Linearly 하게 Seperable 하지 않습니다.
그렇기 때문에 Representational power가 높아지지 못합니다.
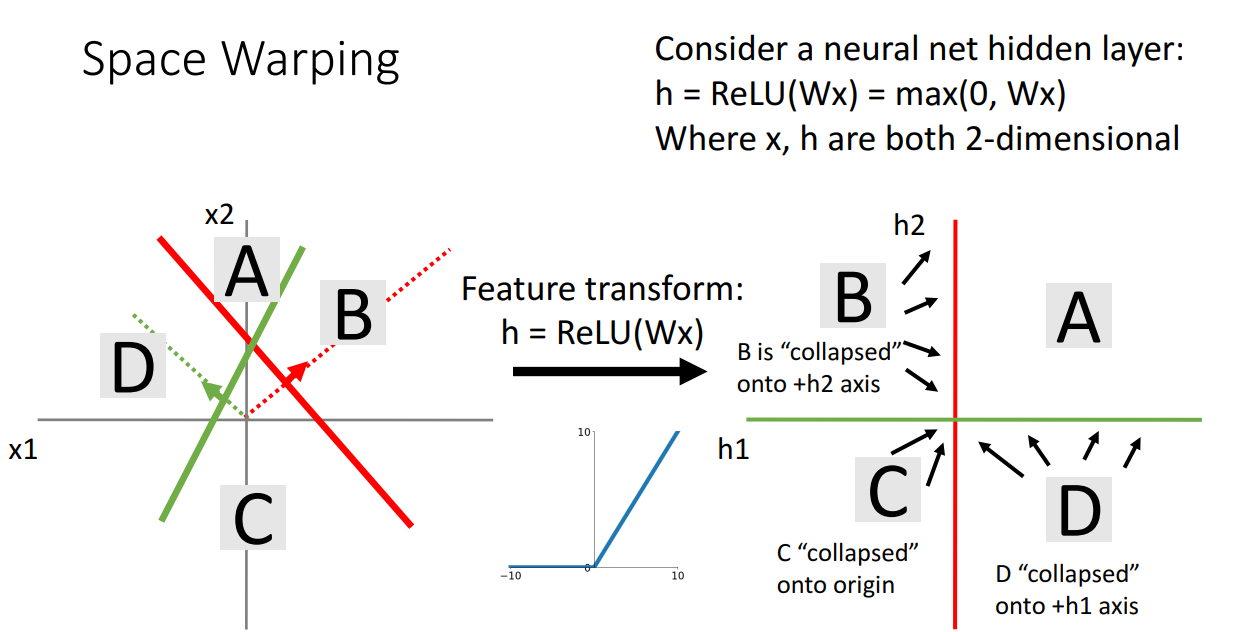
만약 위와 같이 비선형 활성화함수를 사용하면 어떨까요?
이 경우 B, C, D에 있는 점들은 ReLU 함수 정의에 따라 축에 붙어버리게 됩니다.
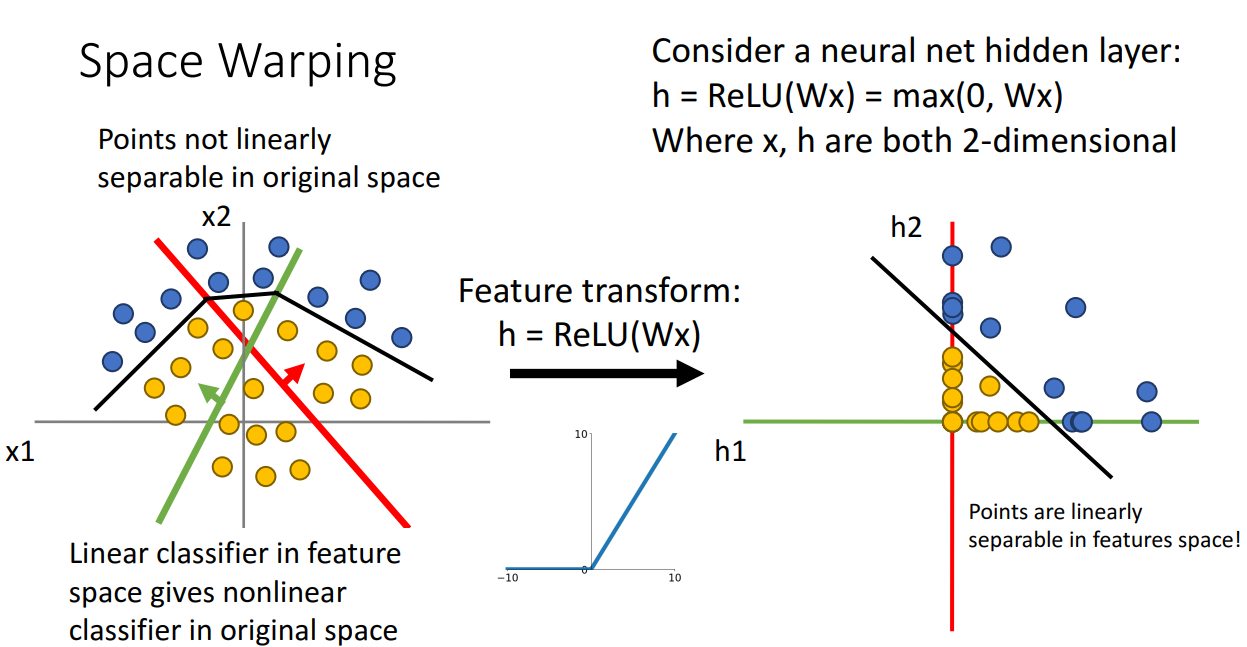
따라서 위와 같이 표현이 되고 이렇게 타점이 된다면 Linearly하게 Seperate하는 선을 찾아낼 수 있고,
Original 좌표 상으로 복원도 가능합니다.
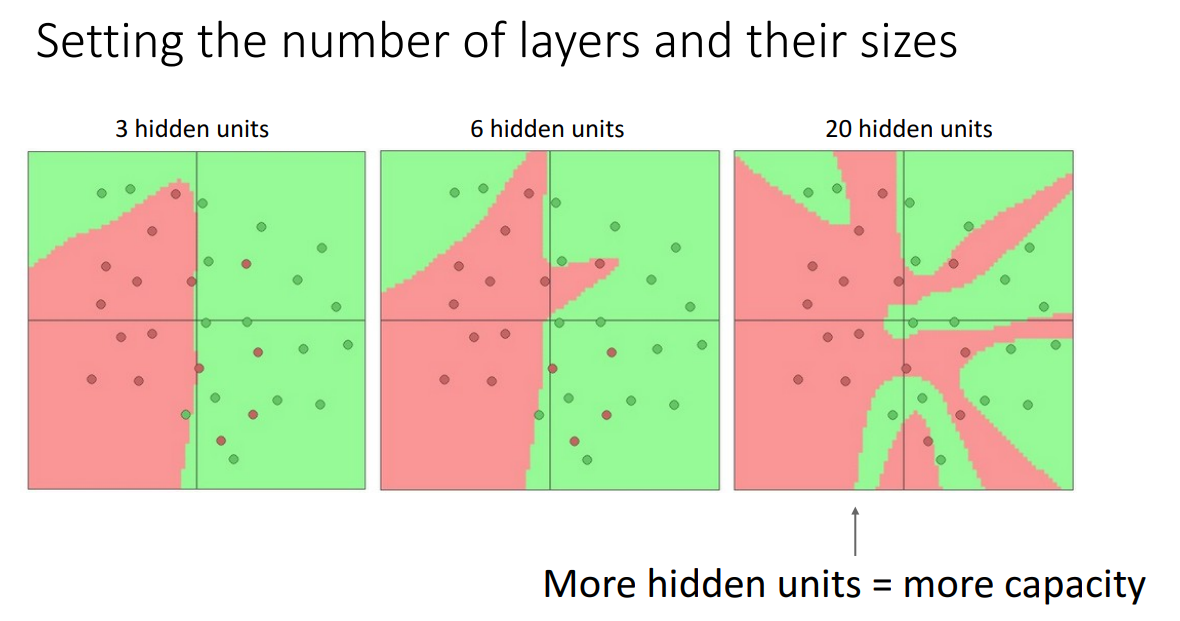
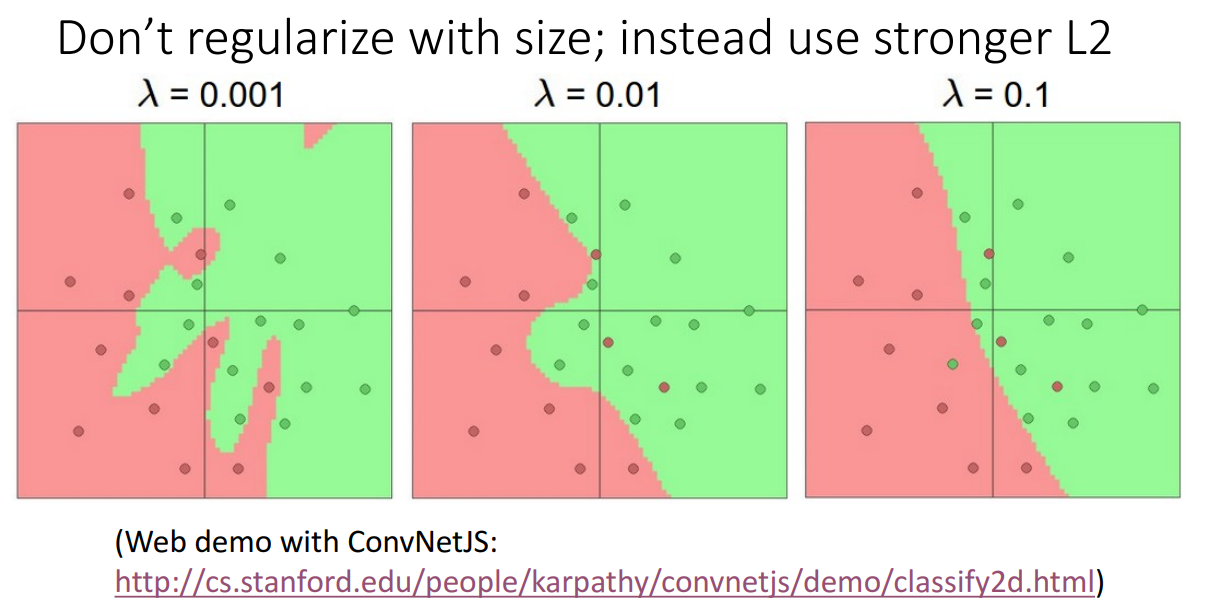
Hidden unit 즉 Weight 을 몇 개 사용할지에 따라서 얼마나 complex하게 학습할 지 결정할 수 있습니다.
왼쪽은 너무 학습이 안되었고 오른쪽은 너무 overfitting 되었습니다.
이러한 상황은 Hidden layer 뿐만 아니라 3장에서 살펴보았던 Regularization에 따라서도 유사하게 보입니다.
Universal Approximation
다음으로 나오는 내용은,
one hidden layer를 가지는 Neural Network는 모든 함수를 근사할 수 있다는 내용입니다.
수식적으로 자세하게 살펴보면 좋지만 간단하게만 표현하면 다음과 같습니다.
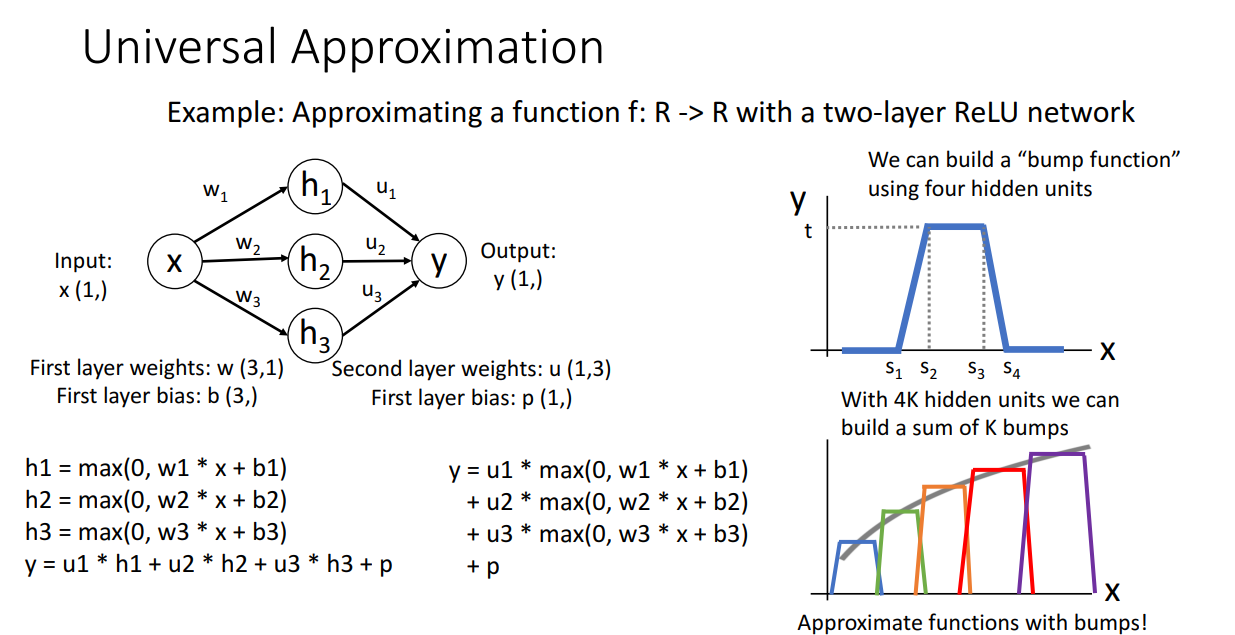
신경망을 통해서 bump function을 만들고 이를 여러개 겹쳐서 비선형 함수를 근사하는 모습입니다.
Convex Functions
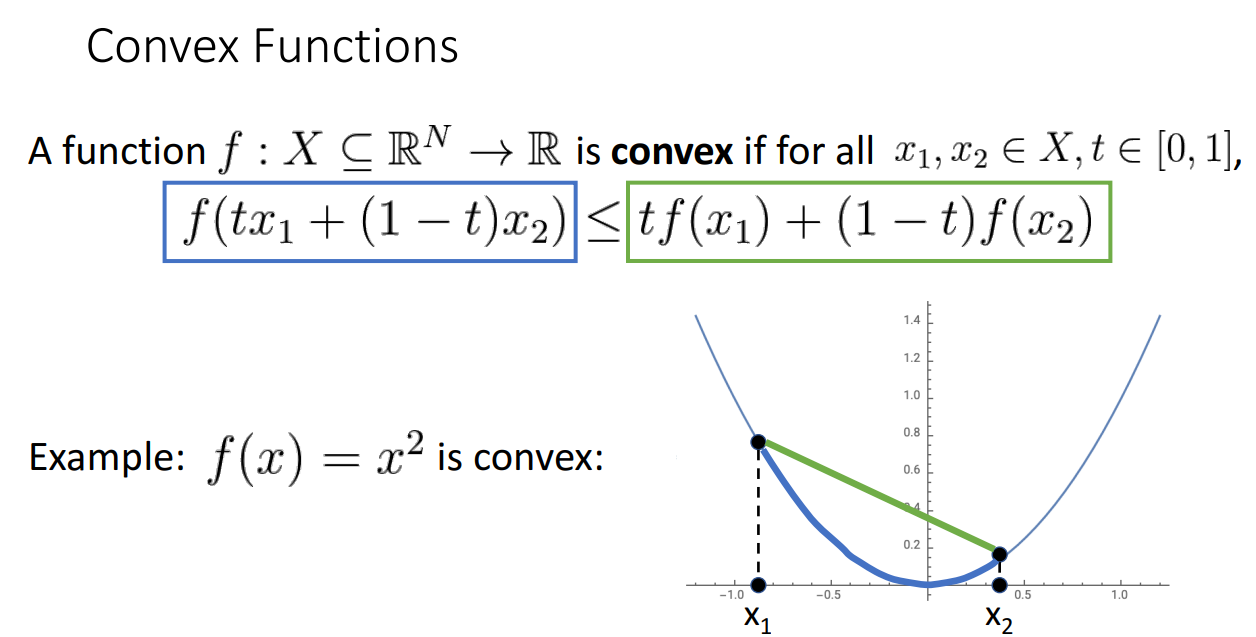
Convex Functions은 Optimization에서 주로 다루는 함수입니다.
위 그림과 같이 파란 부분이 항상 초록 부분보다 작거나 같게 나오는 경우입니다.
cosine 함수는 convex하지 않는 모습을 보이죠.

Convex Function에 대한 개념이 중요한 이유는
convex function은 optimize 하기 쉽다는 것이고 무조건 global minimum으로 수렴한다는 것입니다.
하나 슬픈 점은 대부분의 Neural Networks는 Nonconvex optimization을 해결해야한다는 것이고 따라서 쉬운 작업이 아닙니다.
