
본 게시물은 고려대학교 스마트생산시스템 연구실 2023년 동계 신입생 세미나 활동입니다.
Michigan 대학의 Justin Johnson 교수님의 강의를 공부하는 형식입니다.
관련 유튜브 영상은 여기에서 확인 가능합니다.
Lecture 6: Backpropagation 강의에서는 배울 수 있는 내용은 다음과 같습니다.
- Computational Graphs
- Backpropagation: Examples
- Patterns in Gradient Flow
- Vector or Matrix Backpropagation
- Another View
- Higher-Order Derivatives
Computational Graphs

이전 강의들을 통해서 Nonlinear하게 신경망을 학습하여 분류 Task를 수행하기 위해서는
Loss 함수를 최소화하는 Weight 행렬을 학습하는 과정이 필수적임을 배웠습니다.
해당 Weight 행렬을 학습하는 과정은 최적화 방법론들에 따라서 수행되었고,
모든 최적화 방법론들은 Loss 함수에 대한 Weight 행렬의 Gradients 들을 필수로 계산해야했습니다.

따라서 Weight 행렬의 Gradients를 어떻게 구해야할지 고민해야했고,
좋지 않은 아이디어로는 직접 종이에 써서 계산하는 방식이 있습니다.
해당 방식은 굉장히 귀찮고 많은 계산을 필요로 합니다.
신경망은 상당히 복잡한 구조를 갖고 있기 때문에 모든 과정에서 위와 같이 직접 Gradients를 계산하면
손목이 남아나지 않을 것입니다.
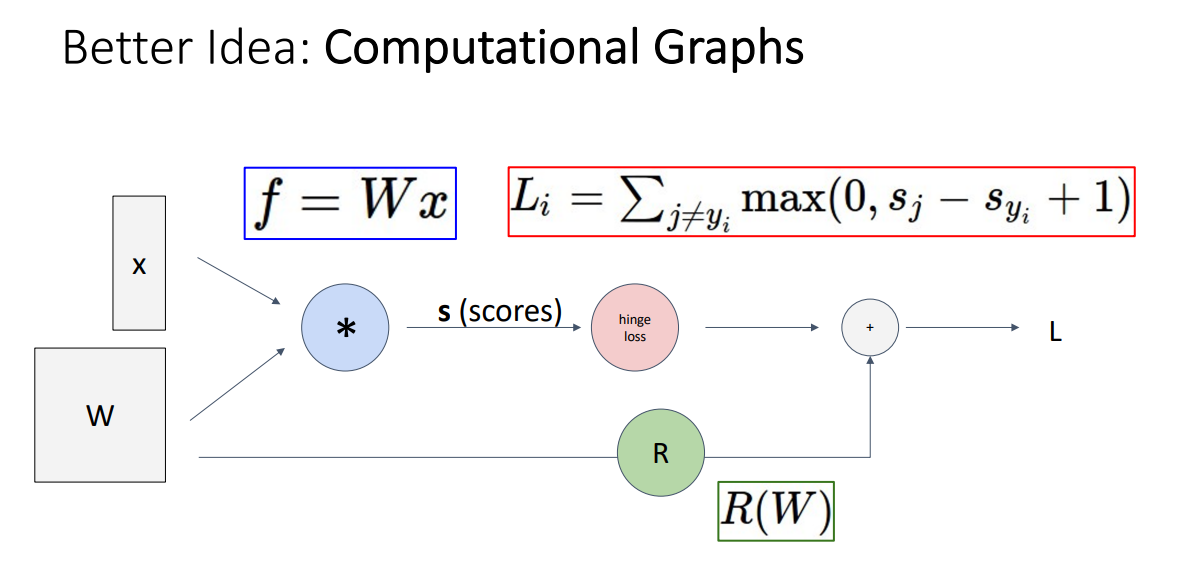
그보다는 훨씬 Fancy하고 계산도 간단하여 학습 속도도 훌륭한 방법이 바로 Computational Graphs 를 활용하는 방법입니다.
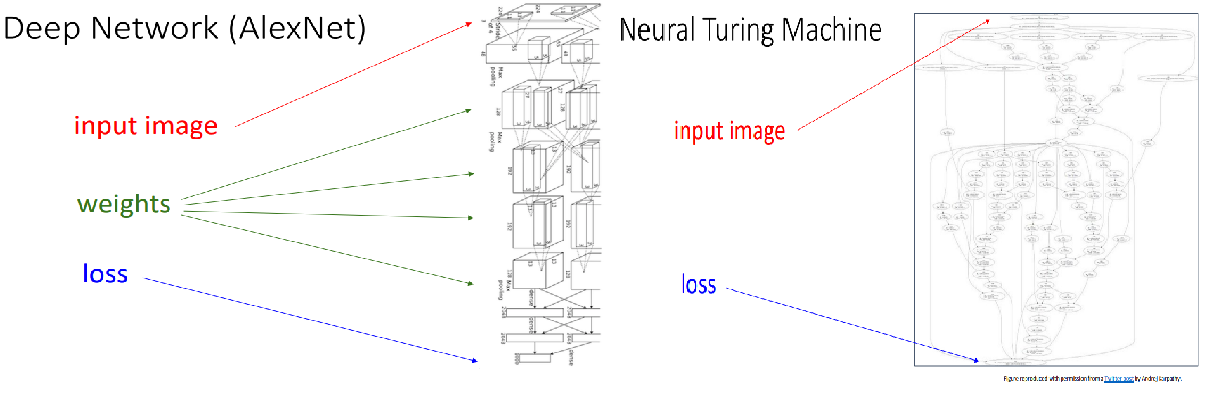
엄청 복잡하게 생긴 AlexNet이나 Neural Turing Machine의 경우에도 Computational Graphs를 활용한 방식으로 Gradients를 구하면 쉽습니다!
Backpropagation: Examples
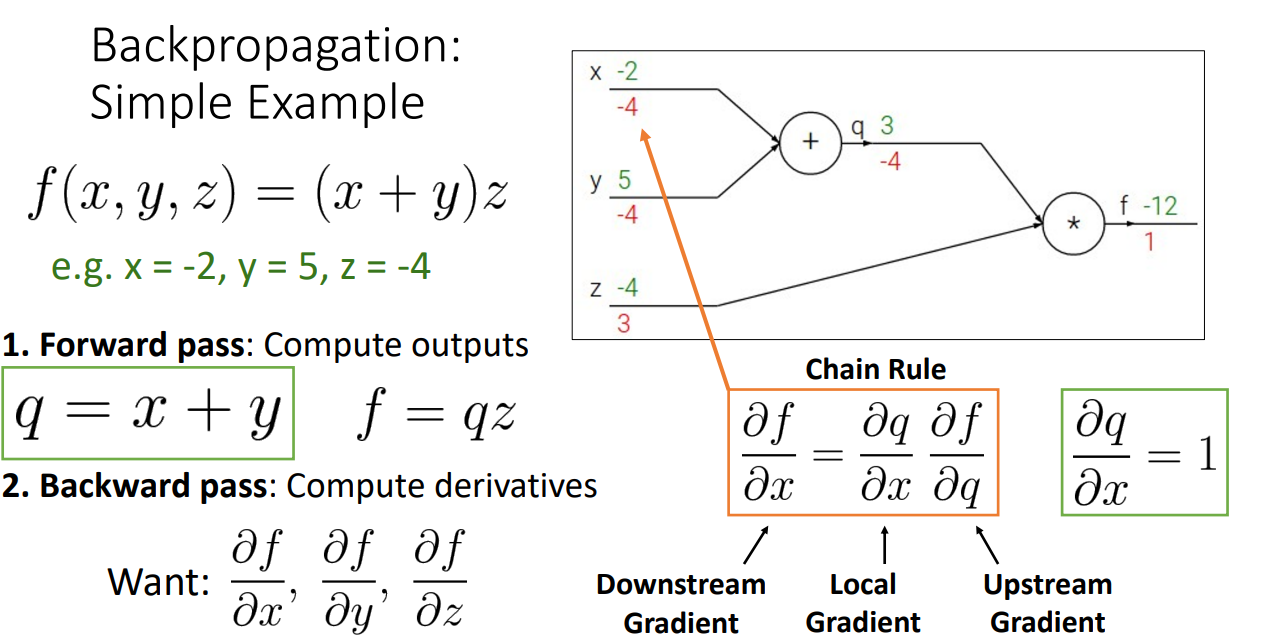
Computational Graphs를 그린 다음 위와 같은 방식으로 Backpropagation(역전파)를 수행한다면
Gradients를 계산할 수 있고 이를 통해 학습이 이뤄집니다.
위의 예시는 가장 간단한 예시입니다.
초록색은 input 값이며, 빨간색은 역전파 시 계산된 derivatives 값들입니다.
해당 과정에서 알 수 있는 점은 Forward(순전파) 시 어떤 수식을 거쳤는지에 따라 역전파시 값의 전달 방식이 다르다는 점과 Chain Rule을 적용할 수 있다는 것입니다.
예시로 주황색 박스를 보면 f output에 대해서 x, y, z 모든 input으로 derivatives를 구해야하는 상황에서,
f에 대한 x의 derivative를 구할 때 곧바로 구하는 것이 아니라 이전 과정에서 구했던 Upstream Gradient와 현 시점의 Local Gradient를 곱하여 구하는 것을 알 수 있습니다.
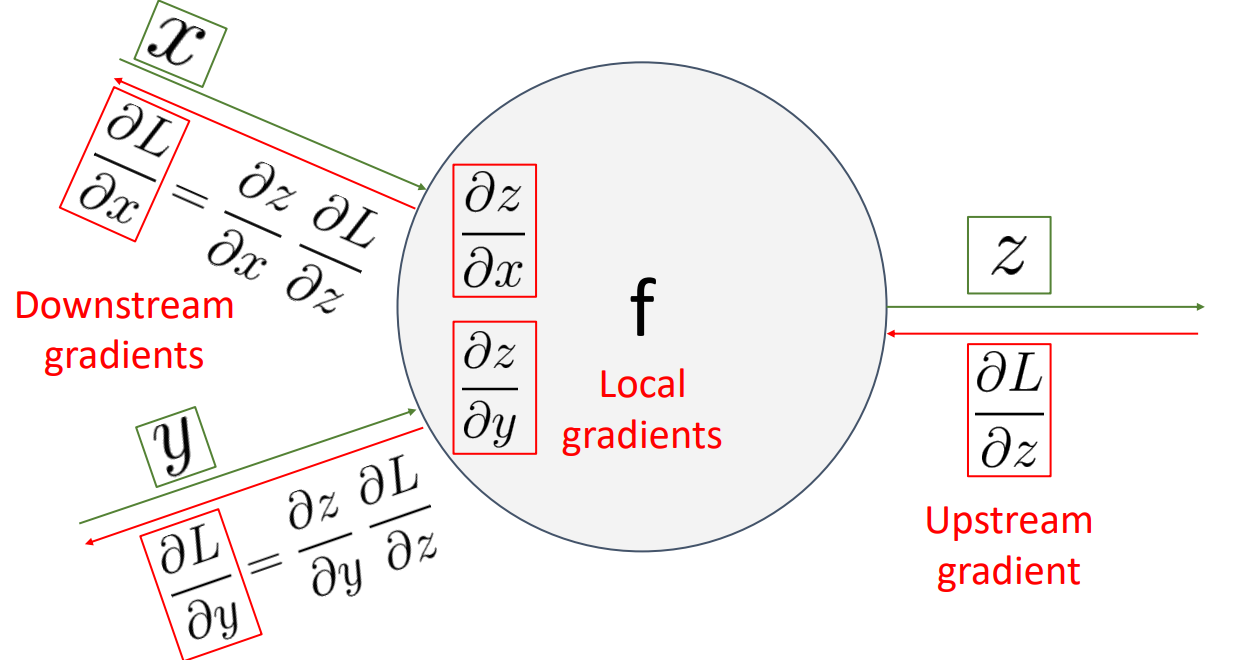
즉 도식화해서 나타내면 위 그림과 같습니다.
다른 서적에서는 해당 과정을 국소적 미분과 Chain Rule을 통해서 Gradients를 구해나가는 과정이라고 설명합니다.
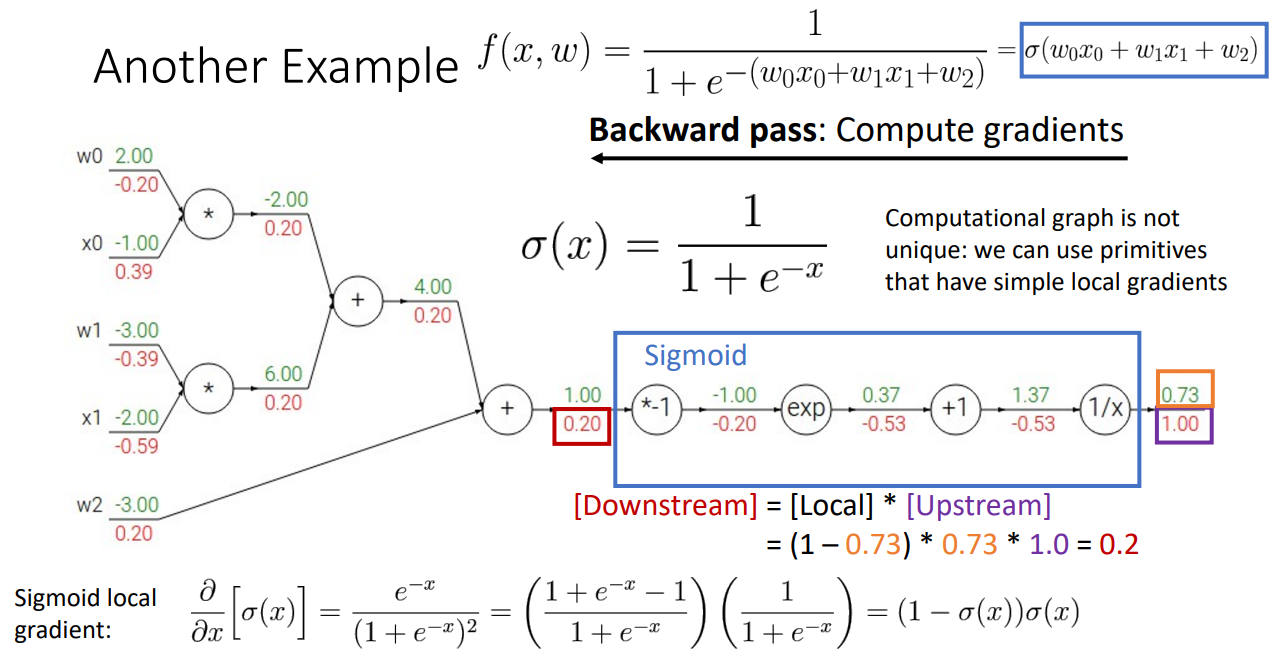
그 다음 예시로는 조금 더 복잡한 신경망 과정에서의 Backpropagation을 설명합니다.
맨 위의 있는 수식의 신경망을 거치게 되고, 그 과정에서 input은 5개 입니다.
따라서 5개의 Gradients를 구해야하는 상황입니다.
이 때 앞서 간단한 예시로 봤듯이 주어진 input으로 순전파를 거쳐 output 값을 산출하고,
반대 방향으로 역전파를 거치며 Gradients 값을 구해나갑니다.
여기서 하나 추가적으로 나오는 것은 비록 국소적으로 미분을 구해서 Chain Rule 에 따라 Downstream Gradient를 구해나가기는 하지만 덩어리로 묶어서 한 번에 Gradients를 계산하는 것도 가능하다는 점입니다.
위 예시에서도 Sigmoid 함수를 거치는 과정을 과정 하나하나씩 역전파시켜도 되지만 그보다는 해당 함수 자체를 미분하여 한 번에 Gradient 를 구하는 수식을 보여줍니다.
따라서 교수님은 Cleverly choose 하기를 조언해주십니다.
Patterns in Gradient Flow
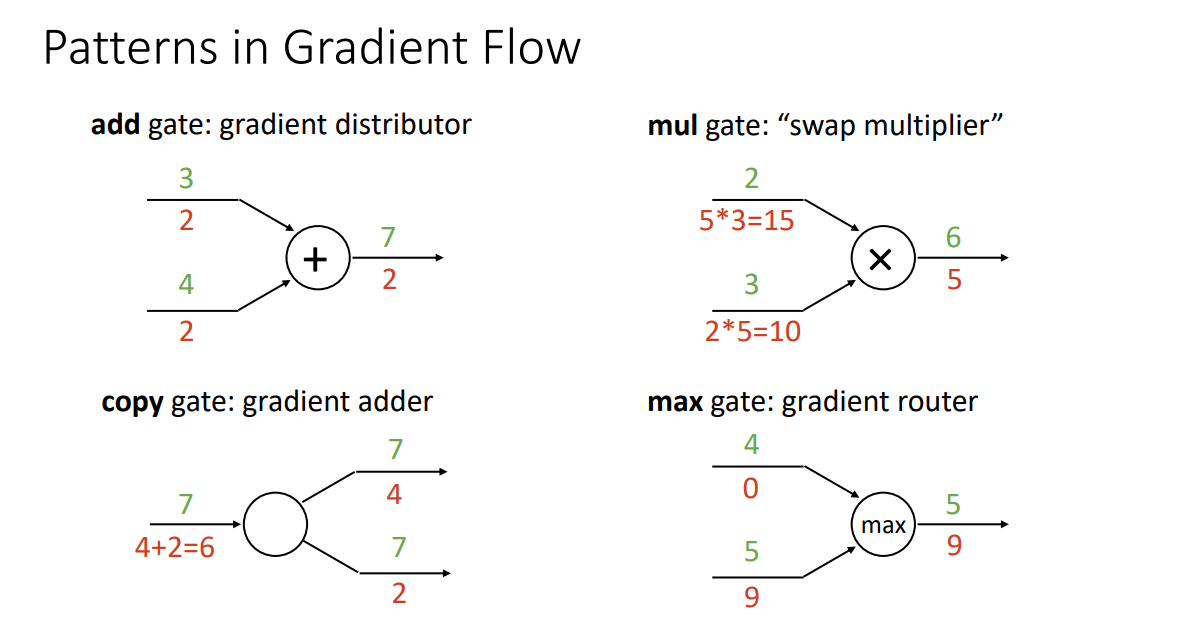
앞선 예시들을 보시면 반복적으로 정형화된 역전파 과정이 보입니다.
- '+' 연산으로 순전파를 진행한 경우 → 역전파 시 Gradient 똑같이 나눠주기
- '복사' 연산으로 순전파를 진행한 경우 → 역전파 시 Gradient 더해주기
(Weight matrix를 복사해서 Regularization에 넣고 싶을 때 쓰는 연산) - '*' 연산으로 순전파를 진행한 경우 → 역전파 시 Gradient 교차해서 곱해주기
- 'max' 연산으로 순전파를 진행한 경우 → 역전파 시 max값 취한 곳으로 보내주고 아닌 곳은 무시(Gradient Router)

파이토치에서 제공하는 Autograd 함수 코드는 위와 같고 상당히 간단한 것을 알 수 있습니다.
Vector or Matrix Backpropagation

앞서 살펴본 역전파 방법은 Scalar 값만을 가지고 예시를 들었습니다.
하지만 input으로 올 수 있는 값은 vector 이며, output 또한 vector 형태로 나올 수 있습니다.
따라서 위 그림과 같이 (1) input이 vector, output이 scalar 인 경우,
(2) input, output 모두 vector 인 경우의 역전파에 대해서 알아보겠습니다.
input, output 모두 vector 인 경우에는 Derivative 값이 Jacobian 행렬입니다.
(1) input이 vector, output이 scalar 인 경우
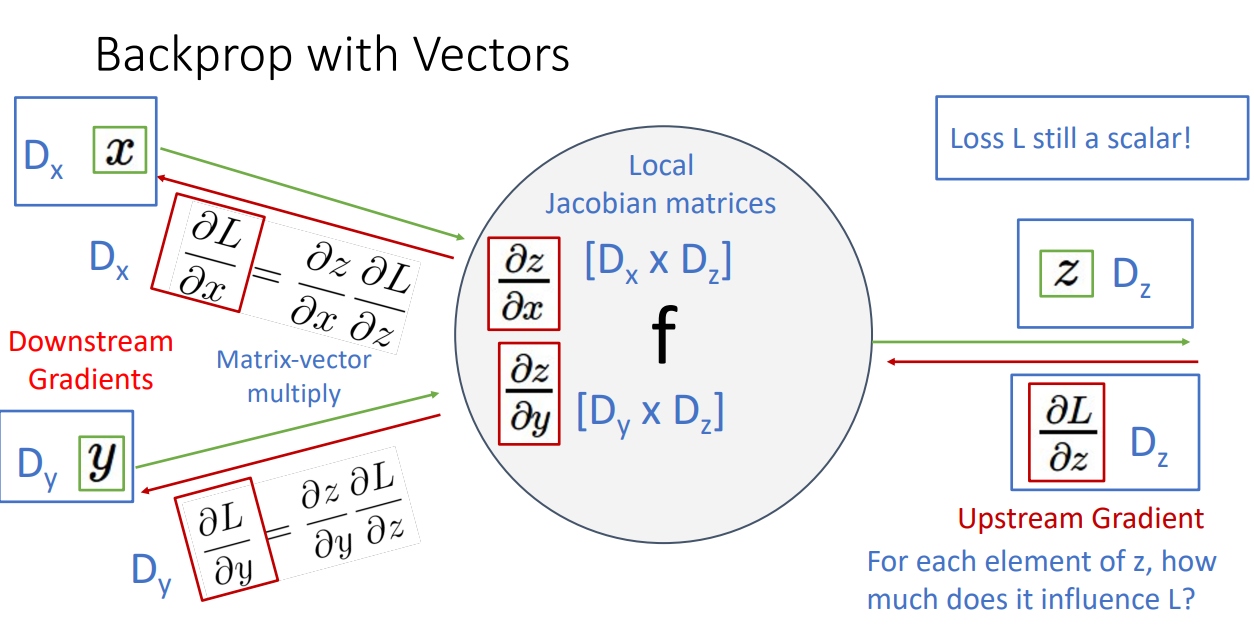
도식화하면 위와 같습니다.
Loss 값은 늘 Scalar 값이며, Upstream Gradient를 구할 수 있습니다. 이를 Local gradients인 Jacobian matrices와 곱해줘서 (Matrix-vector multiply) Downstream Gradients를 구할 수 있습니다.

위 그림은 좋은 예시입니다.
Vector x 가 입력으로 들어가고, 이에따른 output이 나온 상황입니다.
활성화함수는 ReLU를 사용했습니다.
여기서 주목할 점은 역전파시 Local Gradient로 사용할 Jacobian 행렬이 상당히 sparse하다는 것입니다.
행렬곱 연산은 상당히 큰 cost를 필요로하는데, Sparse하다는 특성 덕분에 explicit하게 행렬곱을 하는 것이 아니라 implicit하게 연산 과정을 간략화할 수 있습니다.
따라서 연산이 상당히 trivial 해집니다.
(2) input, output 모두 vector 인 경우
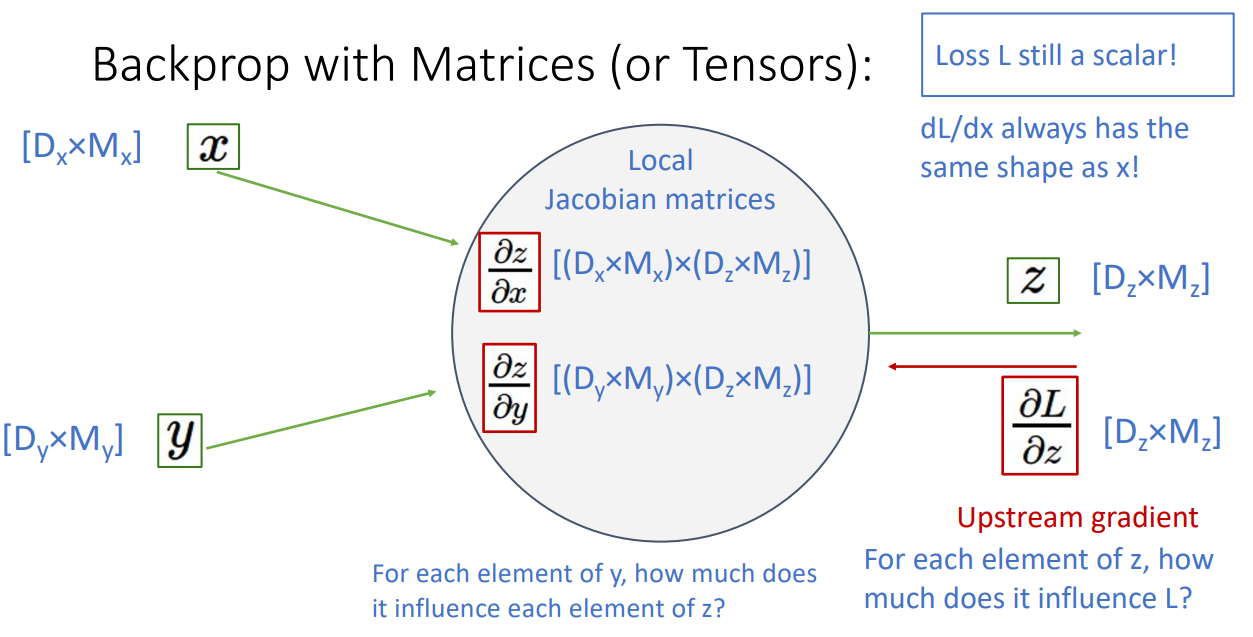
이 경우도 유사합니다. 예시를 들어 설명하겠습니다.
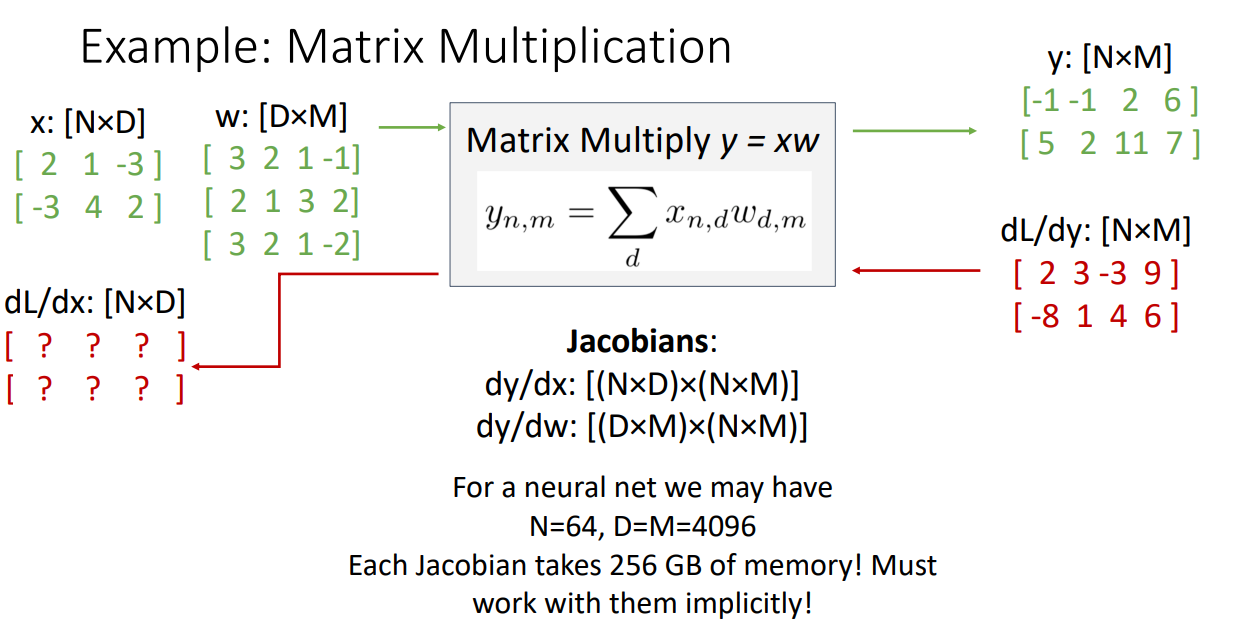
행렬 x와 가중치 행렬 W를 곱하는 연산입니다.
역전파 과정에서 행렬곱은 상당히 헤비한 작업이기 때문에 implicit하게 계산합니다.

계산과정은 강의를 들으시면 이해가 쉽습니다.
계산을 하나하나 해보는 것도 연습이 될 것입니다.
그보다 중요한 것은 Explicit하게 행렬곱하는 것은 비효율적이고 Capacity 상으로 충당이 안되니 implicit하게 도출해야한다는 아이디어입니다.
Another view

역전파 과정이 Chain rule로 진행된다는 사실은 앞서서 살펴봤습니다.
해당 과정은 행렬곱 연산의 반복이기 때문에 상당히 오래걸리는 작업입니다.
따라서 해당 곱을 오른쪽에서 왼쪽으로 수행한다면, 행렬X행렬 연산은 행렬X벡터 연산으로 살짝 더 쉽게 만들 수 있습니다.

그럼에도 불구하고 왼쪽에서 오른쪽으로 계산하고 싶다, 그치만 연산량은 줄이고 싶다.
그런 상황이면 위 Forward-Mode 방식을 선택할 수도 있겠습니다.
해당 방법은 scalar 값을 순전파 가장 앞단에 추가해주는 방법입니다.
이렇게 한다면 행렬X행렬 연산을 피하고 행렬X벡터 연산을 수행하도록 강제할 수 있습니다.
하지만 단점은 Pytorch나 TensorFlow에서 제공되지 않는다는 점입니다.
Higher-Order Derivatives

마지막으로 살펴볼 것은 자주 쓰이지는 않지만, derivative를 구하는 연산을 1차미분을 여러번 반복하기 보다는 2차 이상의 미분으로 수행하겠다는 아이디어입니다.
이 경우에는 Local Gradients 행렬로 Jacobian 행렬 대신 Hessian 행렬이 사용됩니다.
