
본 게시물은 고려대학교 스마트생산시스템 연구실 2023년 동계 신입생 세미나 활동입니다.
Michigan 대학의 Justin Johnson 교수님의 강의를 공부하는 형식입니다.
관련 유튜브 영상은 여기에서 확인 가능합니다.
Lecture 7: Convolutional Networks 강의에서는 배울 수 있는 내용은 다음과 같습니다.
- Convolution Layer
- Shape of Output
- Pooling Layer
- LeNet-5
- Batch Normalization
Convolution Layer
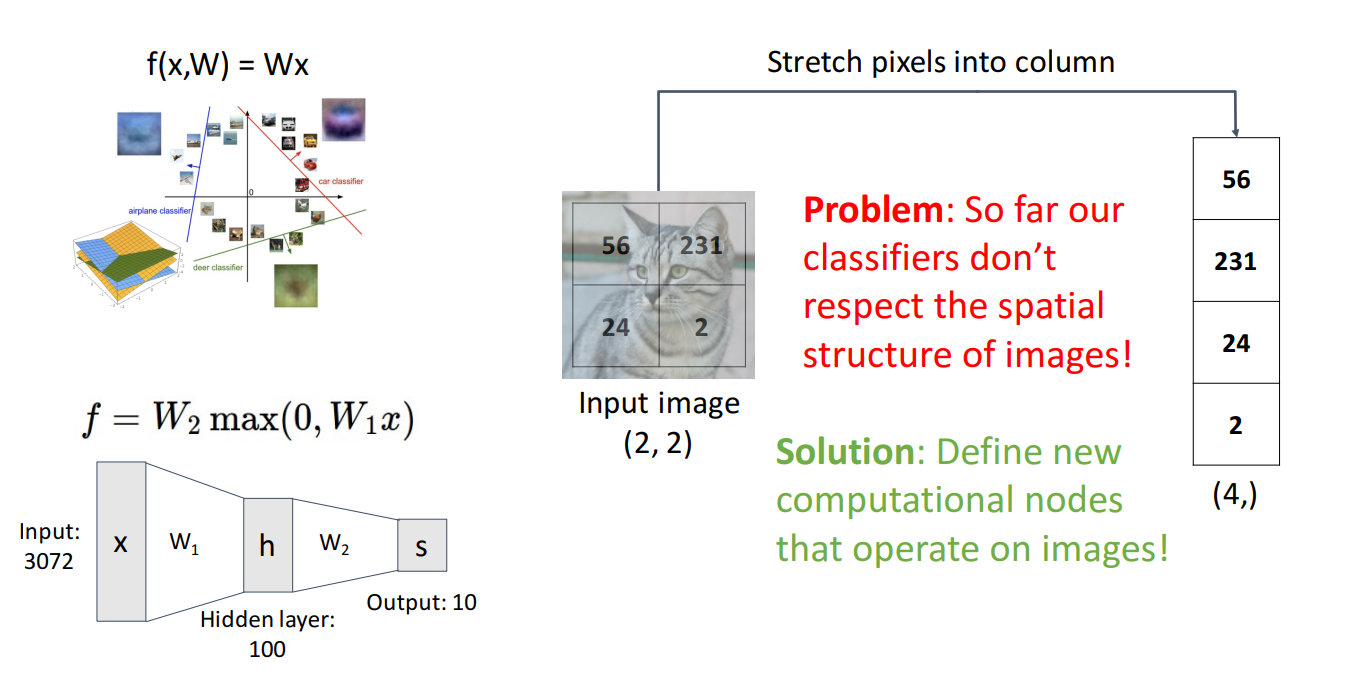
지금까지 Linear Classifier, MLP를 배우면서 항상 문제가 하나 있었습니다.
이미지의 Spatial 구조를 무시한채 분류를 수행한 것입니다.
Spatial한 구조를 flatten한 column을 신경망에 넣곤 했습니다.
그보다는 더 나은 방식은 이미지의 Spatial 구조를 유지하도록 하는 새로운 Operator를 도입하는 것입니다.
그것이 바로 Convolution Layers 입니다.
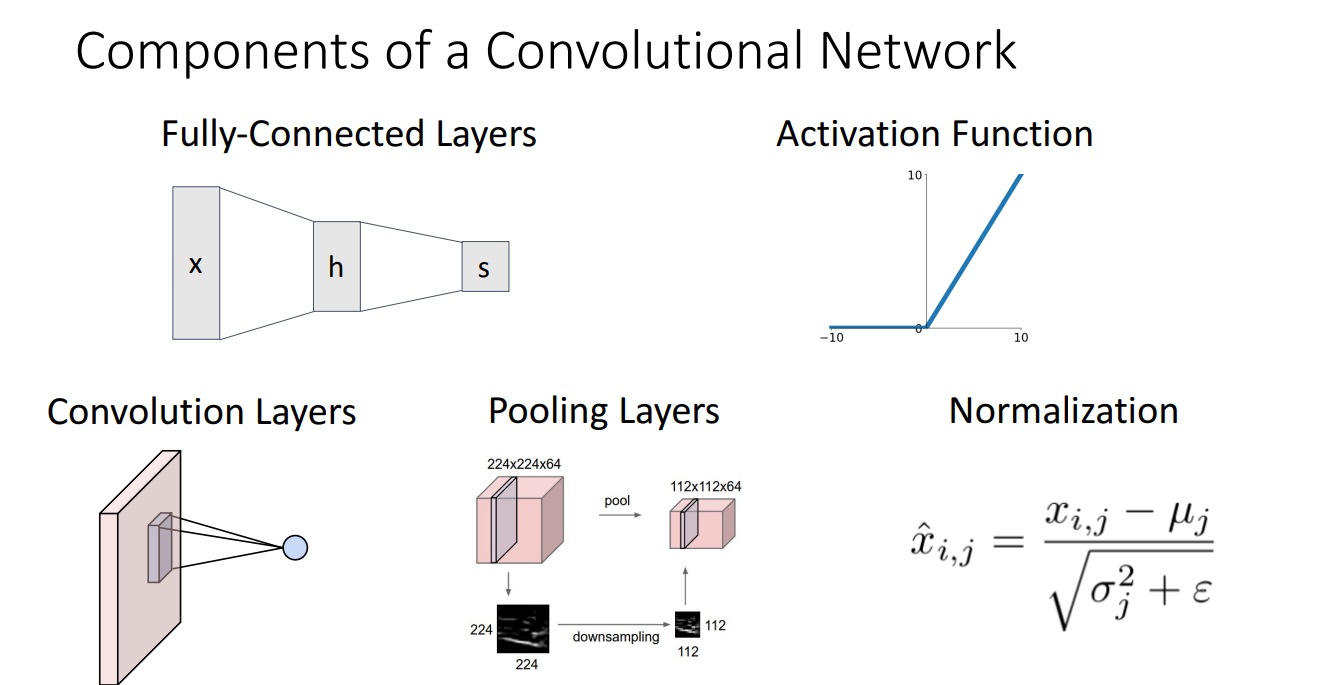
Convolutional Network의 구조는 위와 같습니다.
Fully-Connected Layers와 Activation Function은 기존에 배운 것과 같지만,
여기서 새롭게 소개되는 구조는 Convolution Layers, Pooling Layers, Normalization 입니다.
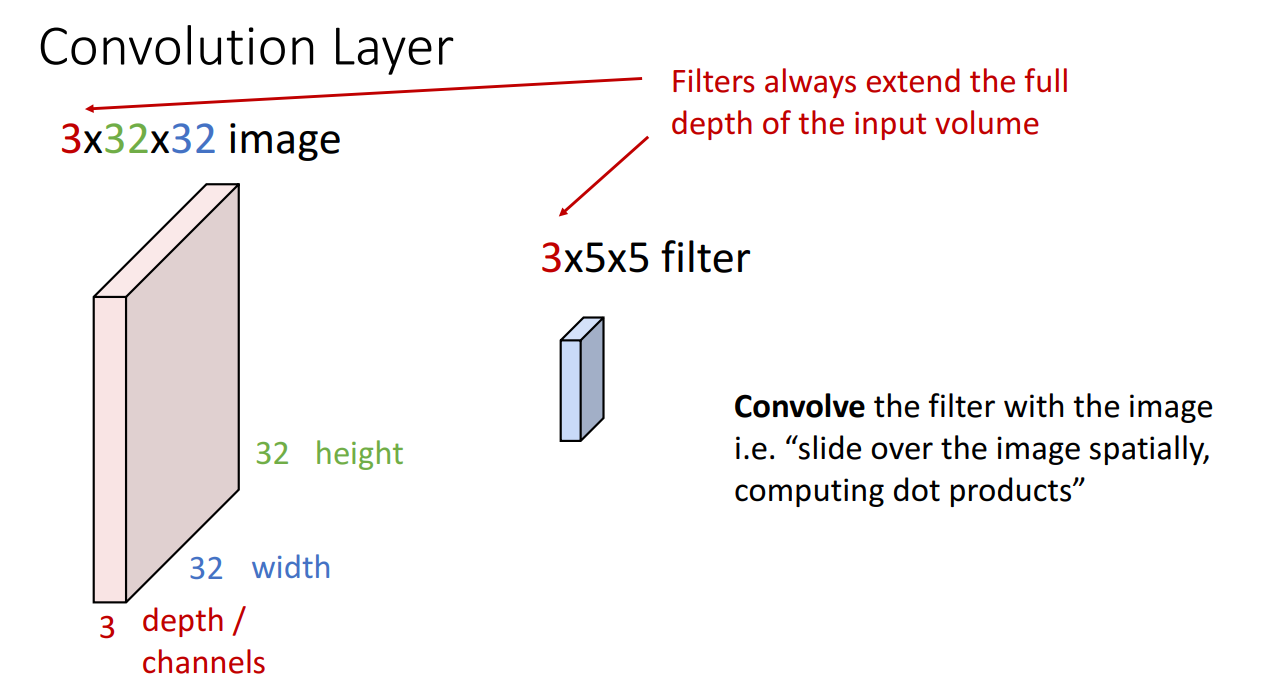
먼저 Convolution layer 부터 살펴보겠습니다.
위 예시의 경우 input 이미지가 32x32 크기의 RGB 3 channel 입니다.
이 때 Convolutional filter의 개수는 항상 같은 채널(여기선 3)로 맞춰주고 크기는 사용자가 정하는 임의의 크기(3x3, 5x5, etc) 로 설정해줍니다.
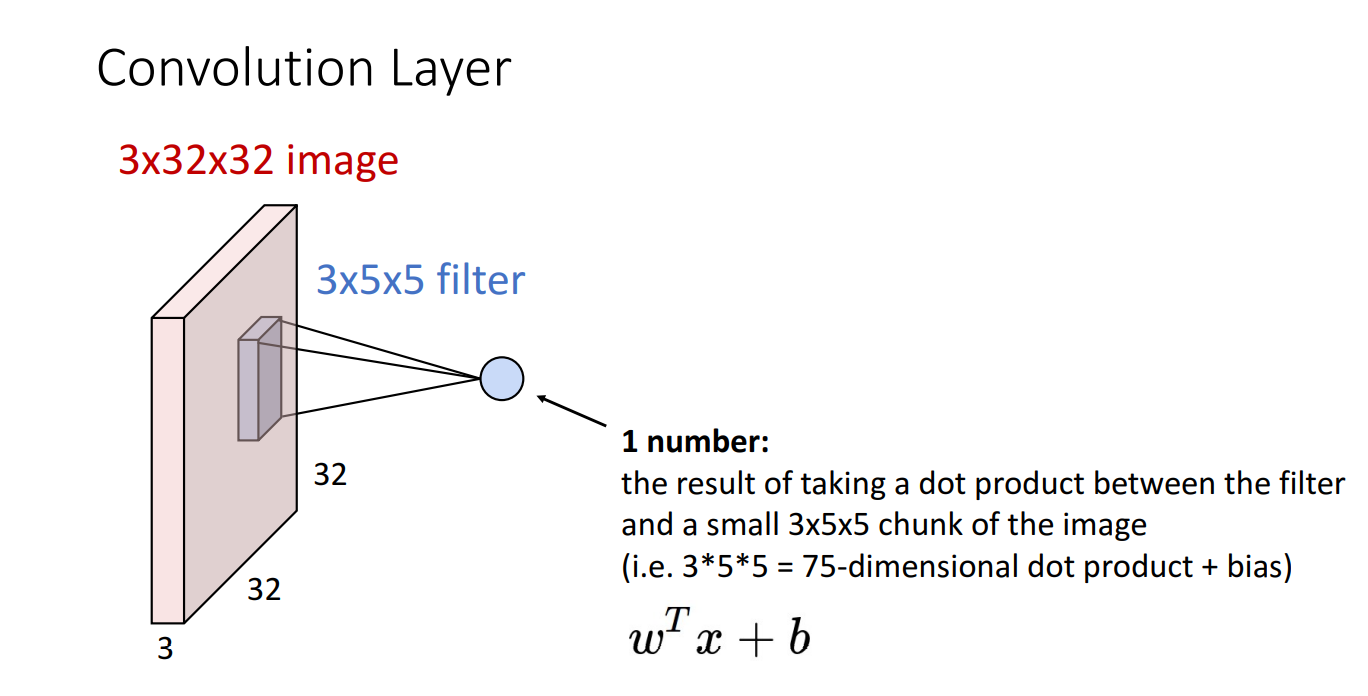
위와 같이 필터가 한 번 거칠때 필터의 크기만큼 dot product 연산을 거치게 되고 1개의 숫자가 계산됩니다.
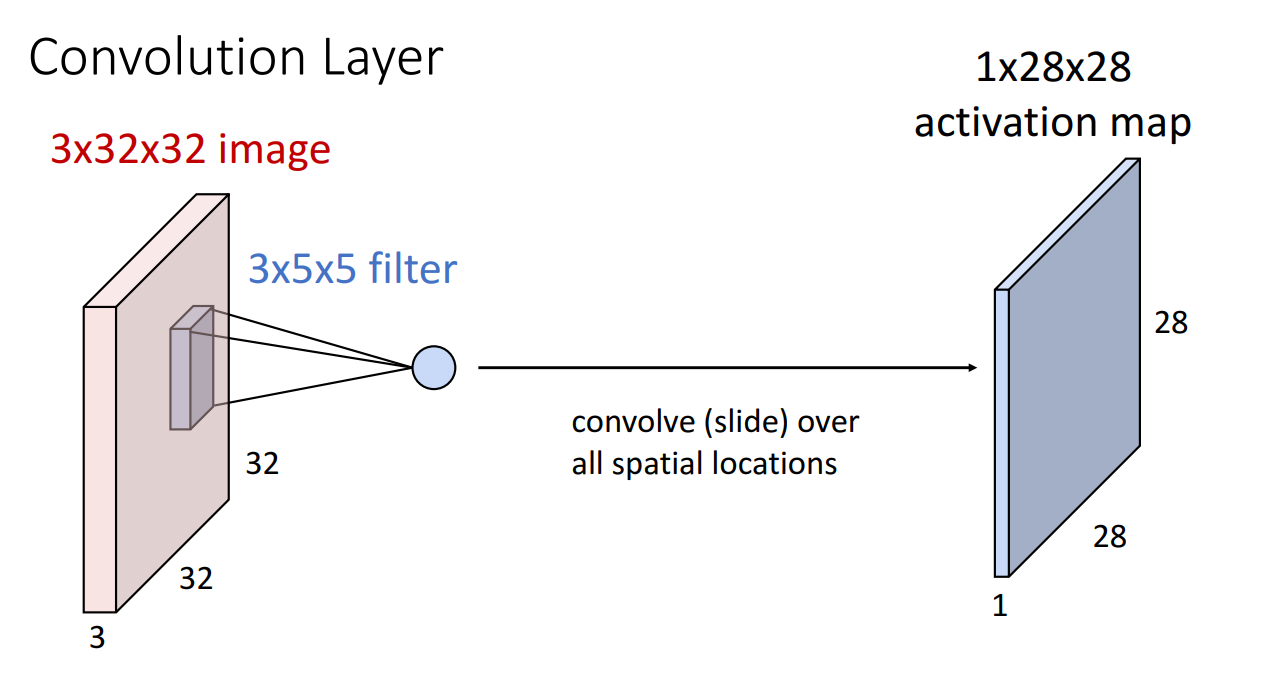
필터가 한번 쭉 돌면 위와 같이 activation map이 산출됩니다.
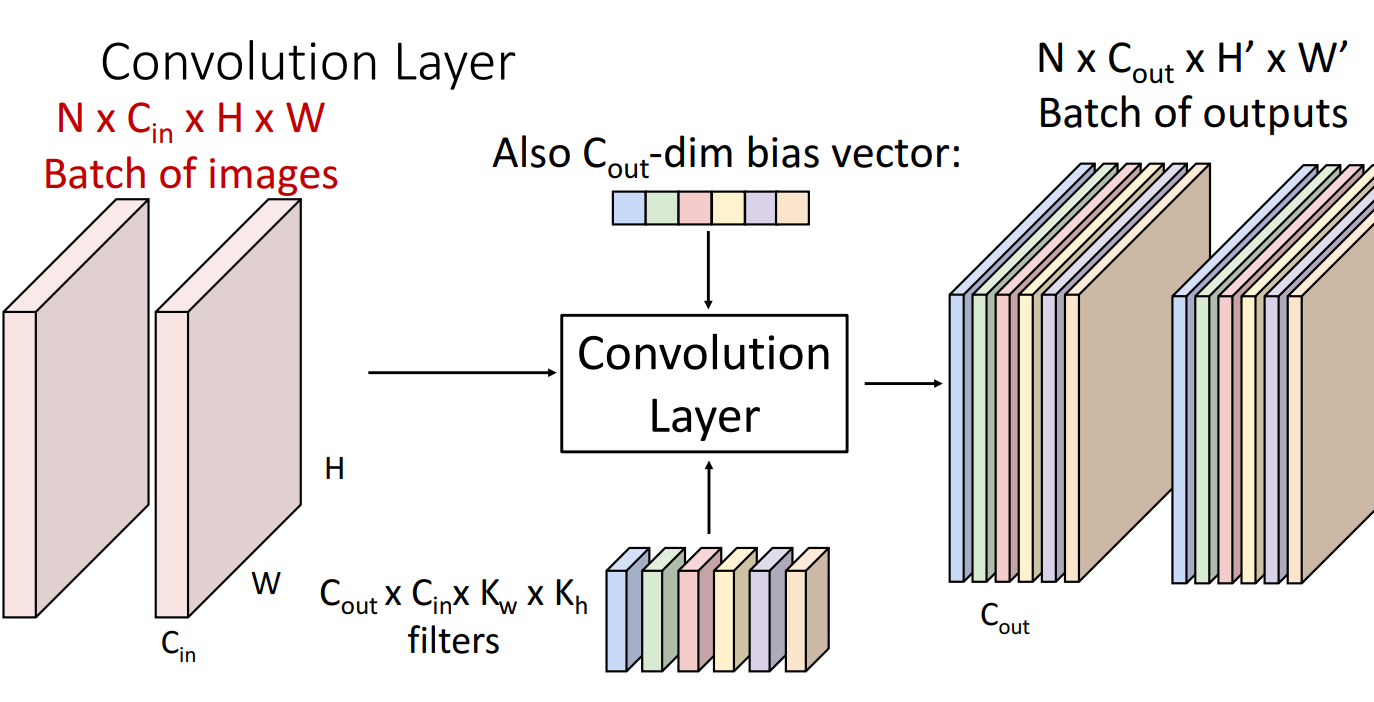
일반화해보면 위와 같습니다.
총 N 크기 배치의 이미지들이 개의 필터들은 거쳐서 총 개의 activation map이 N 배치만큼 생성되는걸 볼 수 있습니다.
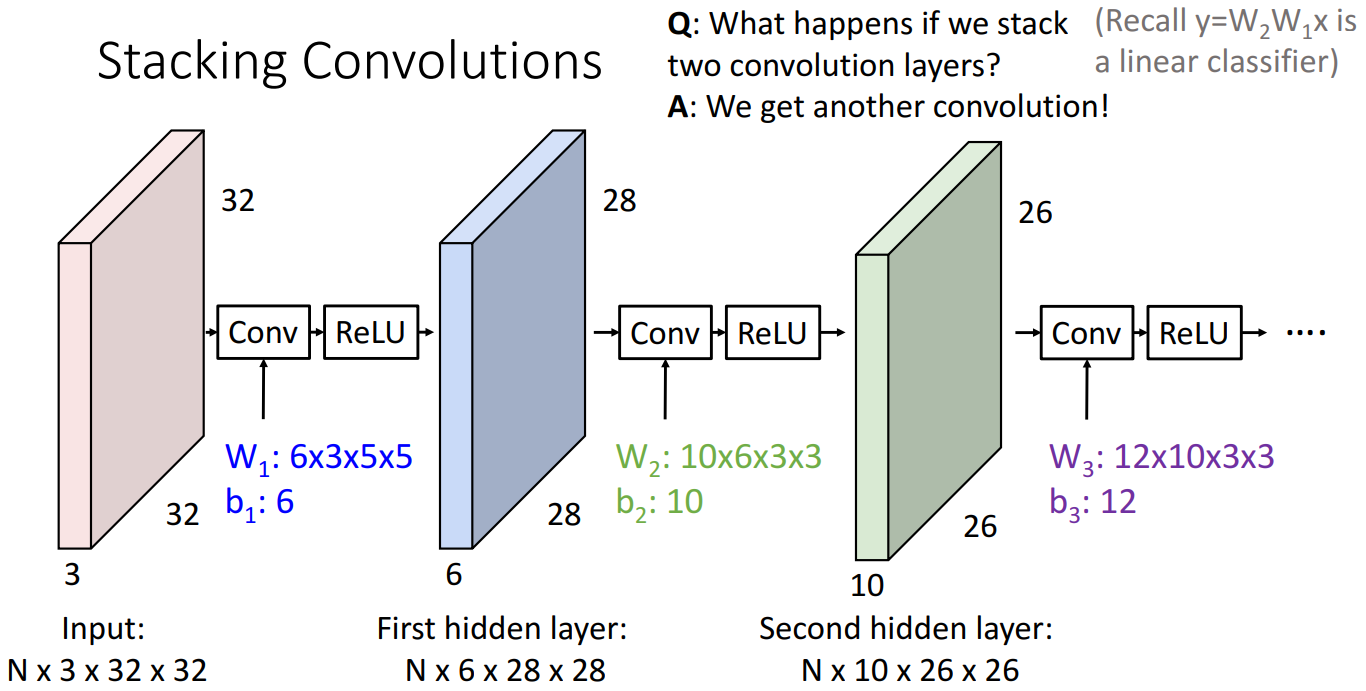
Convolution layer를 여러개 쌓는 모습입니다.
여기서 주목할 점은 중간중간에 Nonlinear한 activation function을 삽입한 것입니다.
활성화 함수를 삽입하지 않는다면 linear classifier때 살펴봤던 것 처럼 여러개를 쌓은 효과를
보지 못하기 때문입니다.
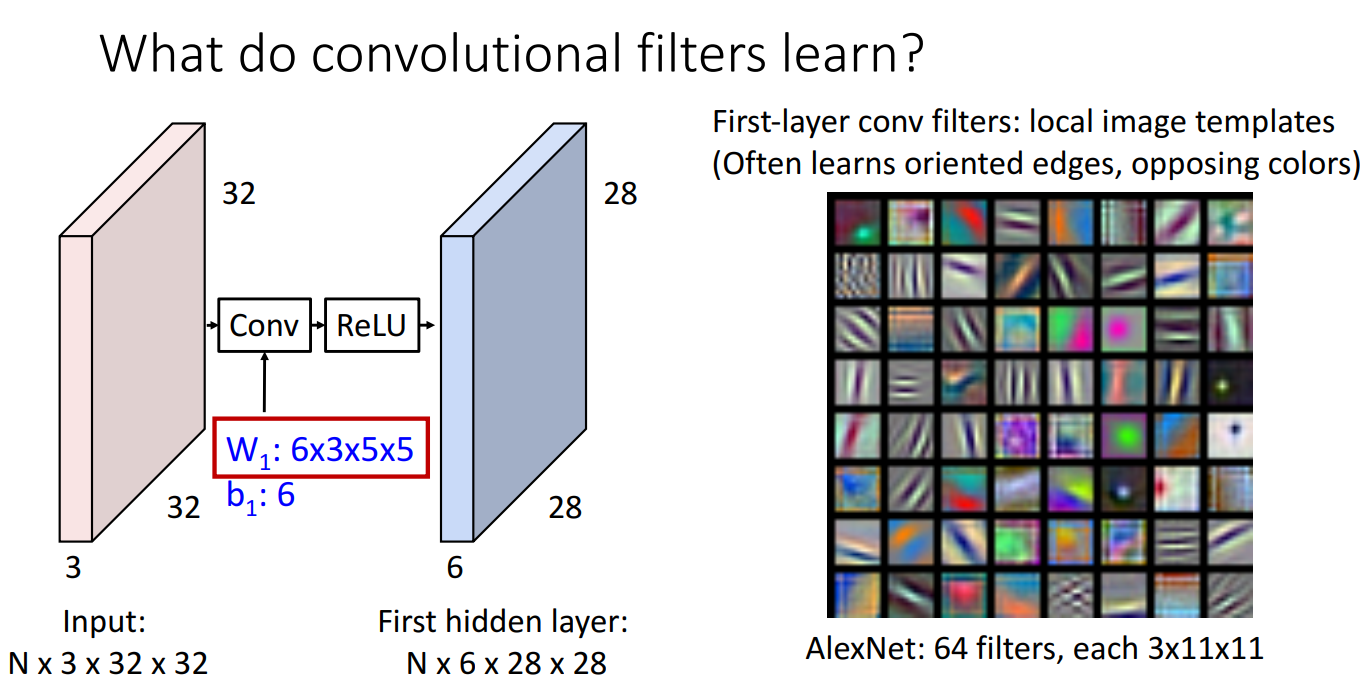
왜 Convolution filter를 써야하는지에 대한 설명은 위와 같습니다.
Edge, opposing color 와 같은 local image template을 시작 단계의 Conv filter가 잘 포착하는 것을 알 수 있습니다.
기존의 Linear Classifier나 MLP는 Class를 구분하는 template을 학습하는데에 반해 Conv Filter는 Spatial한 정보를 학습하는 장점이 있습니다.
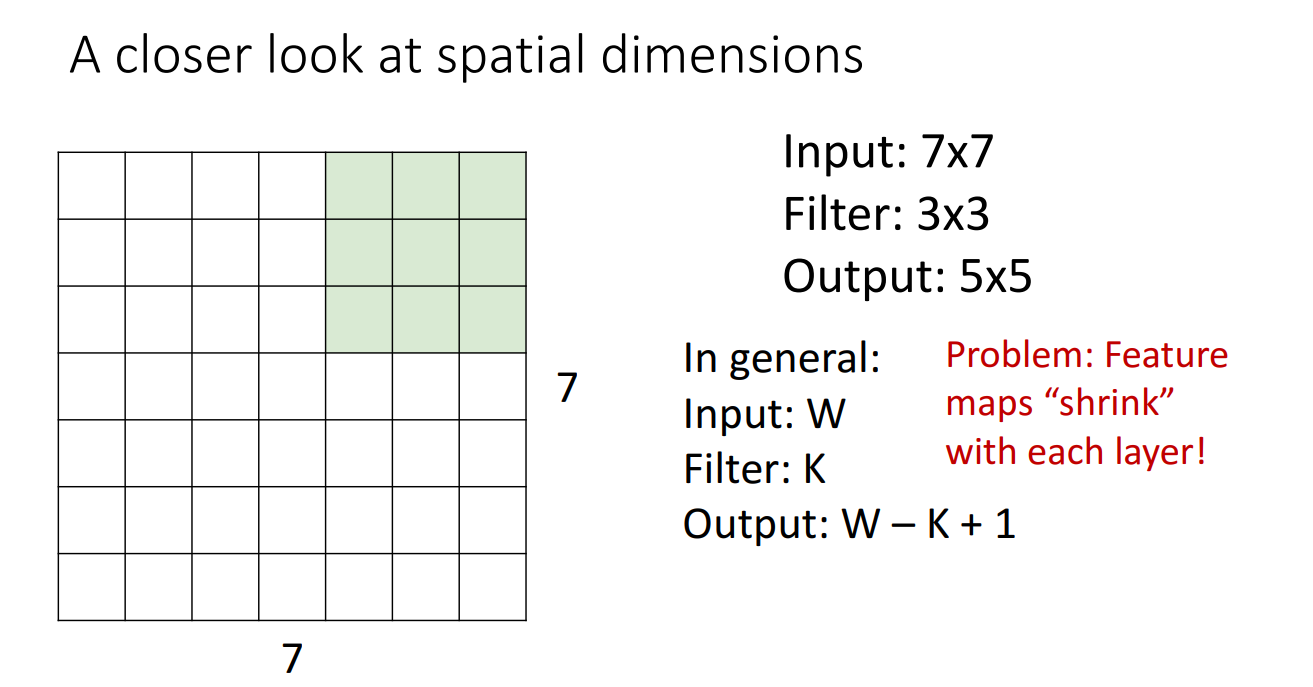
Conv filter가 원본 이미지를 지나가면서 Dot product 연산을 거치고 Output activation map을 산출할 때는 한 가지 문제가 있는데 Feature map이 Shrink 된다는 점입니다.
여러 개의 Conv filter를 거친다면 Feature map은 너무 작아져버릴 것입니다.
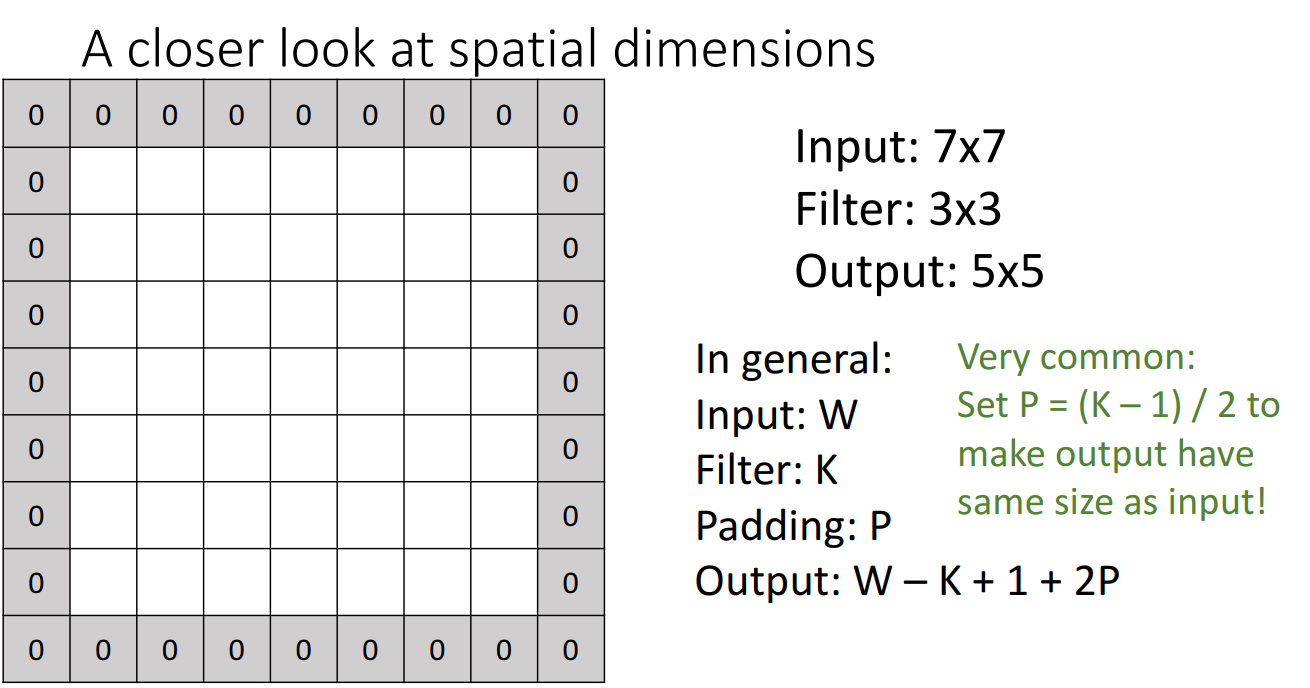
앞서 말한 문제점을 해결하는 여러 방법들이 있는데 그 중 첫번째는 패딩(Padding)을 추가하는 것입니다.
패딩은 원본 이미지의 겉에 특정 숫자들을 둘러싼 뒤 필터가 해당 테두리들도 연산에 포함하도록 하여 Feature map의 크기를 줄어들지 않도록 하는 방법입니다.
일반적으로 0을 테두리에 두르는 Zero-Padding이 주로 쓰입니다.
패딩을 몇겹으로 쌓을지는 선택이지만 로 설정하면 input 이미지와 같은 크기의 output activation map을 얻어낼 수 있습니다.
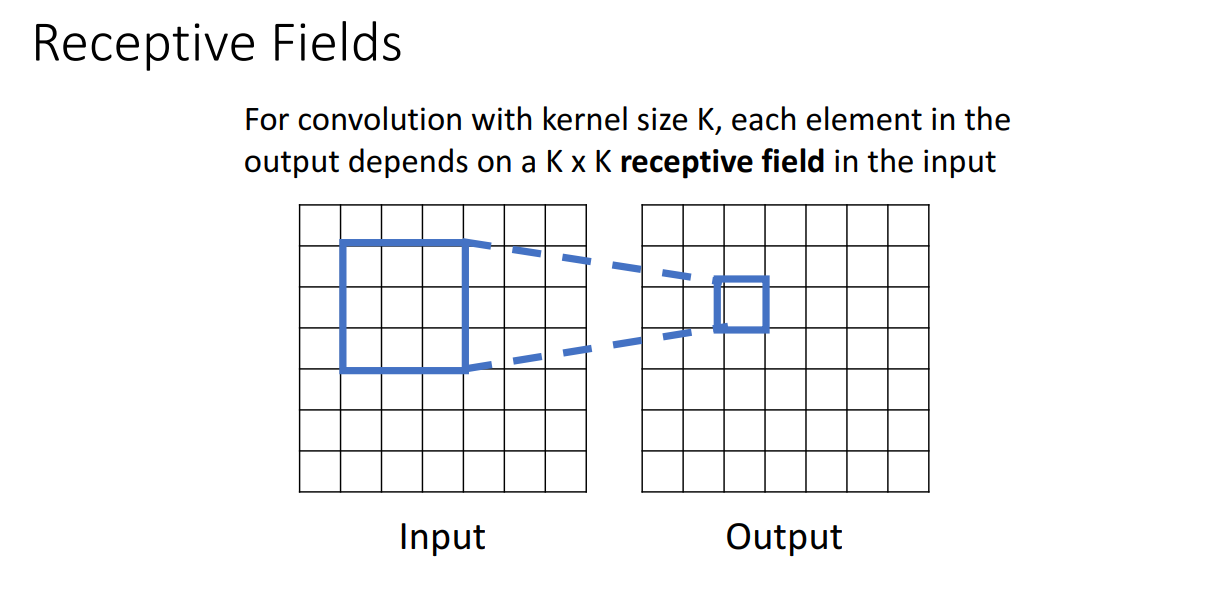
추가적으로 Receptive Fields 라는 개념도 소개되는데 이는 kernel size가 KxK 일때,
output activation map의 특정 하나의 픽셀은 input 이미지의 KxK receptive field에 의존한다는 것입니다.
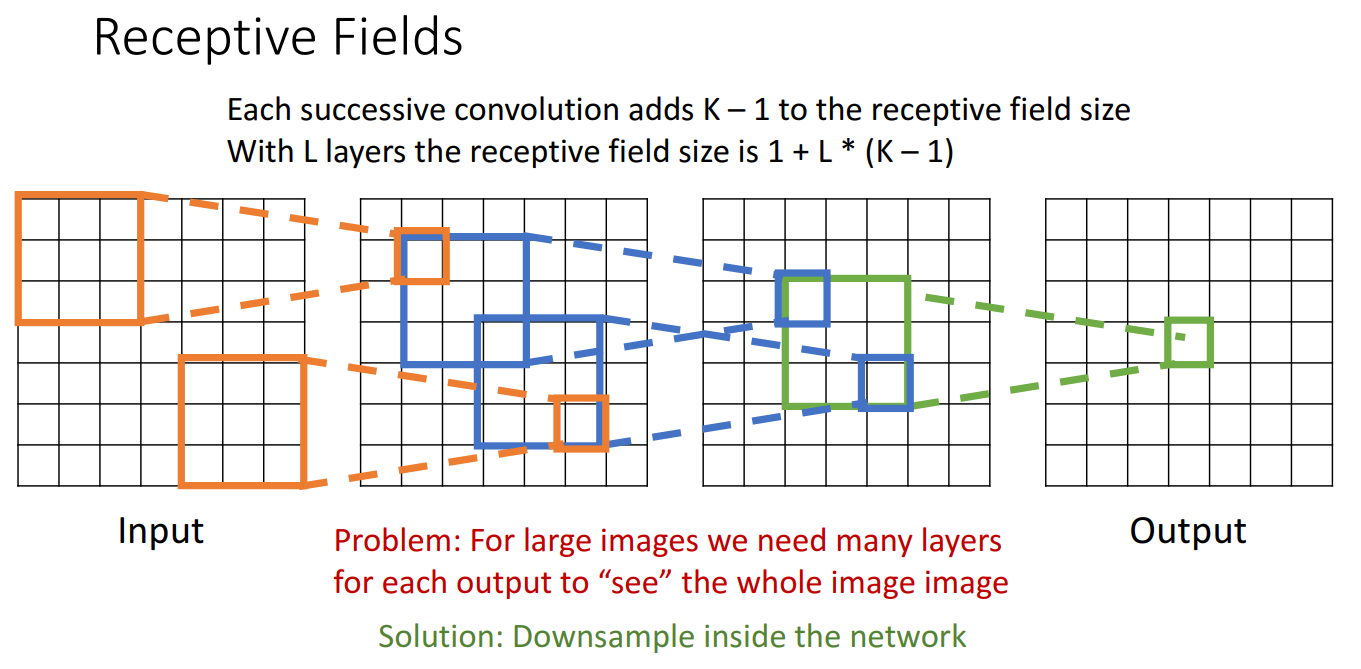
해당 개념과 관련해서 생기는 하나의 문제점은 Output에서 global context 정보를 담기 위해서는 너무 많은 layers가 필요하다는 것입니다. 특히 고해상도 이미지 상황에서는 더욱 심각하구요.
이를 해결하기 위해 Downsample 하는 방법이 고안됩니다.
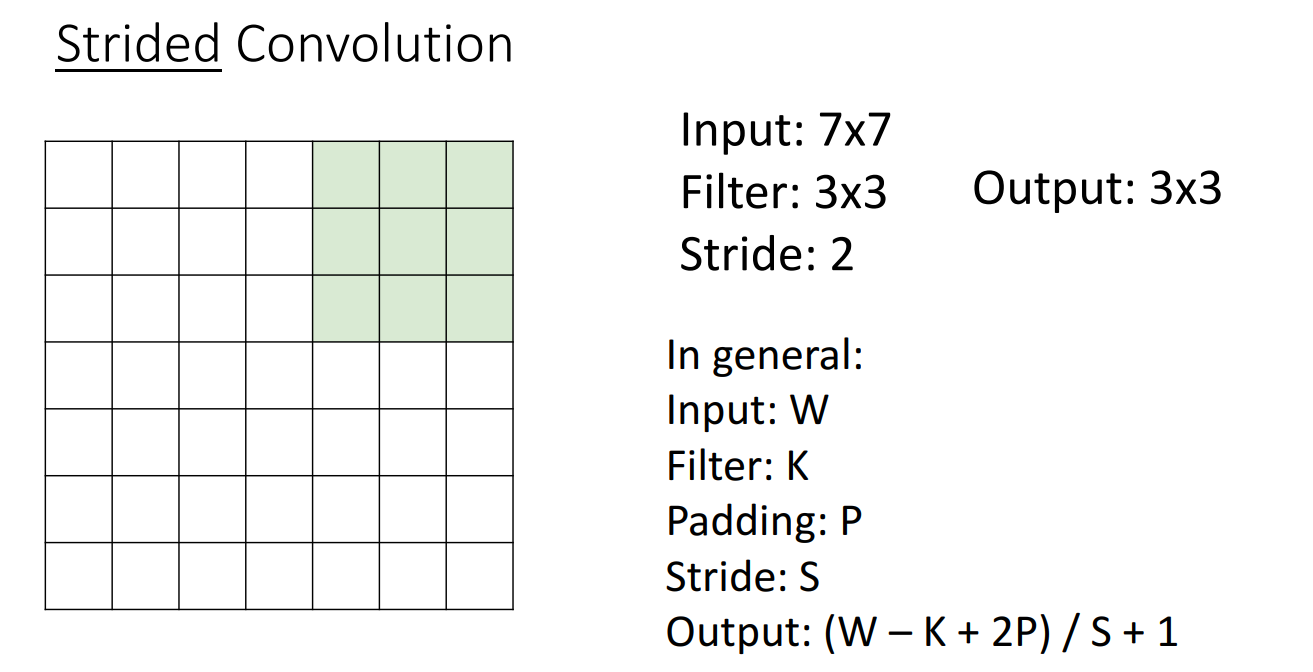
그래서 나온 방법은 Stride를 적용하는 것입니다.
기존의 Conv filter는 한칸씩 이동하면서 activation map을 산출해냈지만,
두칸씩, 세칸씩 뛰어넘으면서 Conv filter를 거치면 Downsample 된다는 아이디어입니다.
Shape of Output

지금까지 살펴본 개념으로 Input 이미지가 Conv Filter를 거칠 때 Output activation map의 크기는
어떻게 나올지를 계산해낼 수 있습니다.
먼저 공식은 입니다.
위 예시로 살펴보면 적용하는 필터의 개수만큼 activation map이 나오고,
크기는 로 계산됩니다.
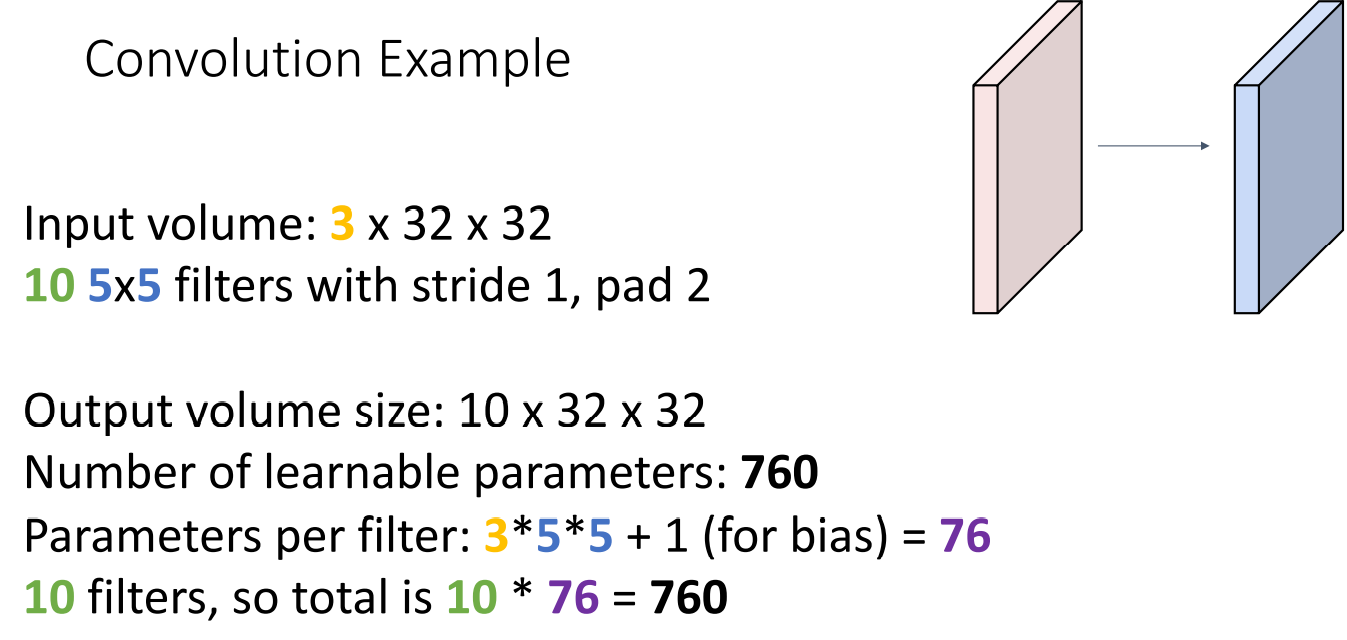
추가로 학습해야할 파라미터의 개수도 계산할 수 있습니다.
먼저 하나의 필터는 의 Dot product와 합 연산을 거쳐야 하고
필터의 개수는 10개 이므로 의 파라미터를 학습해야합니다.

연산량도 계산할 수 있는데요.
앞서 Output activation map의 크기를 로 구했고 하나하나의 요소 값을 구하기 위해서는
Dot product 연산을 거쳐야합니다. 따라서 이를 모두 곱하면 768K 정도의 연산량이 필요합니다.
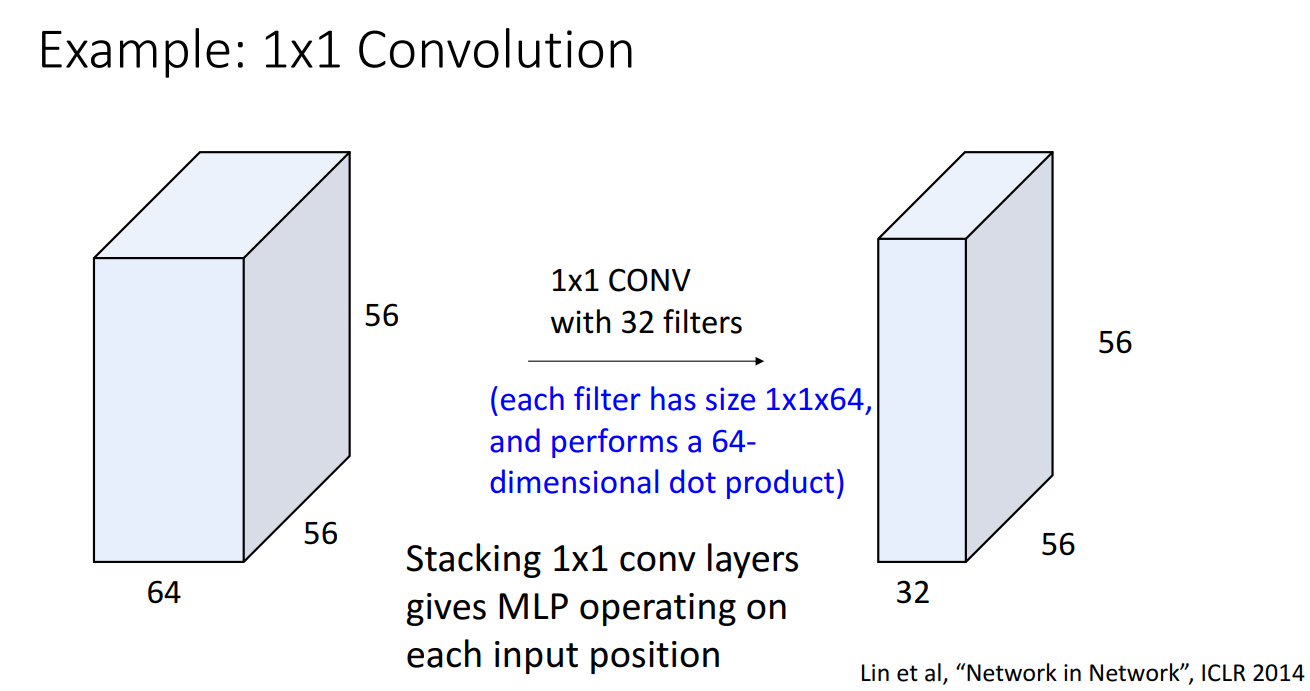
강의에서는 1x1 Convolution도 소개되었습니다.
1x1 filter를 거치면 지역적 정보를 보는데에 무슨 소용이냐 하실 수 있지만,
이는 MLP 와 유사한 역할을 수행하면서도 input 의 위치 정보를 해치지 않는다는 장점이 있어서,
여러 유명한 CNN 구조에서 잘 사용되는 방법입니다.

Convolution layer에 대한 정리입니다.
네트워크를 설계할 때 위 정리와 같이 차원을 맞춰서 설계하면 편합니다.
기본적인 Setting 값도 추천해주셨습니다.
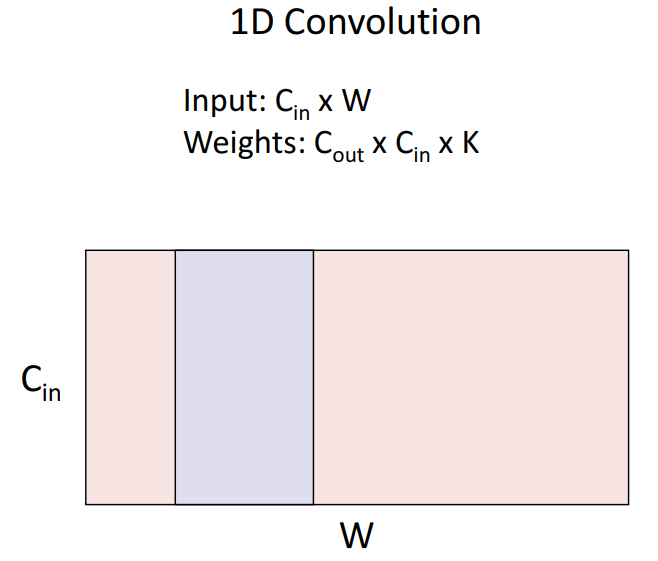
2D Conv 외에도 1D Conv filter를 거치는 경우도 소개되었는데요,
이는 Sequence 구조를 갖는 시계열 데이터, 오디오 데이터에서 큰 장점이 있는 방법입니다.
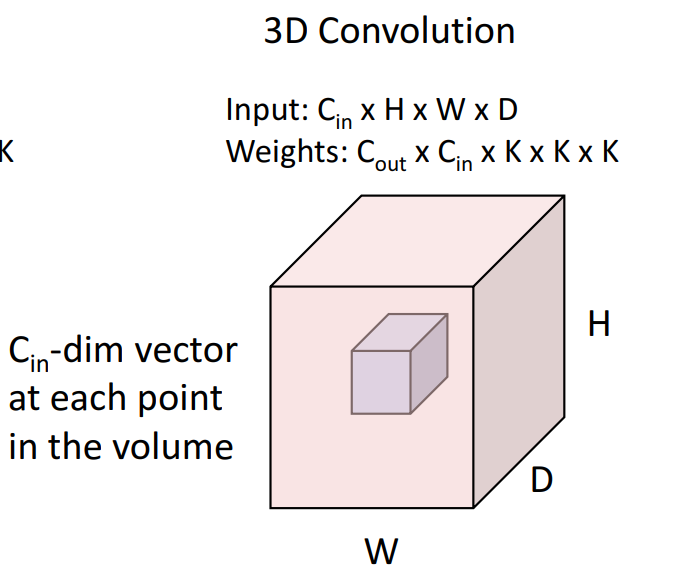
3D Conv도 존재합니다.

모두 파이토치에서 손 쉽게 사용할 수 있습니다.
Pooling Layer
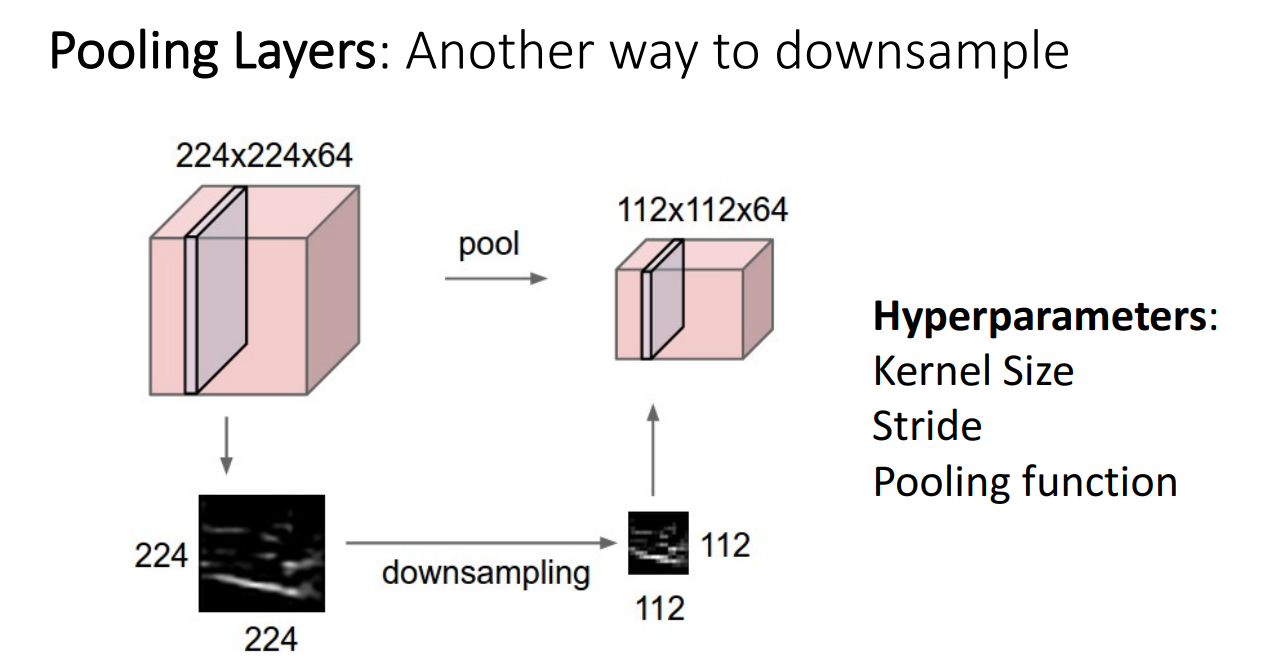
지금까지 Convolutional Layer를 통해, 그 과정 중 Stride 를 적용하여 Downsample하는 방법을 살펴보았습니다.
Convolutional Layer 말고도 CNN 구조에서는 Downsample 하는 기능을 가진 구조가 있는데,
바로 Pooling Layer 입니다.
위 그림에서도 알 수 있듯, Pooling Layer는 하이퍼파라미터가 Kernel size, stride, pooling function으로 이루어져있습니다.
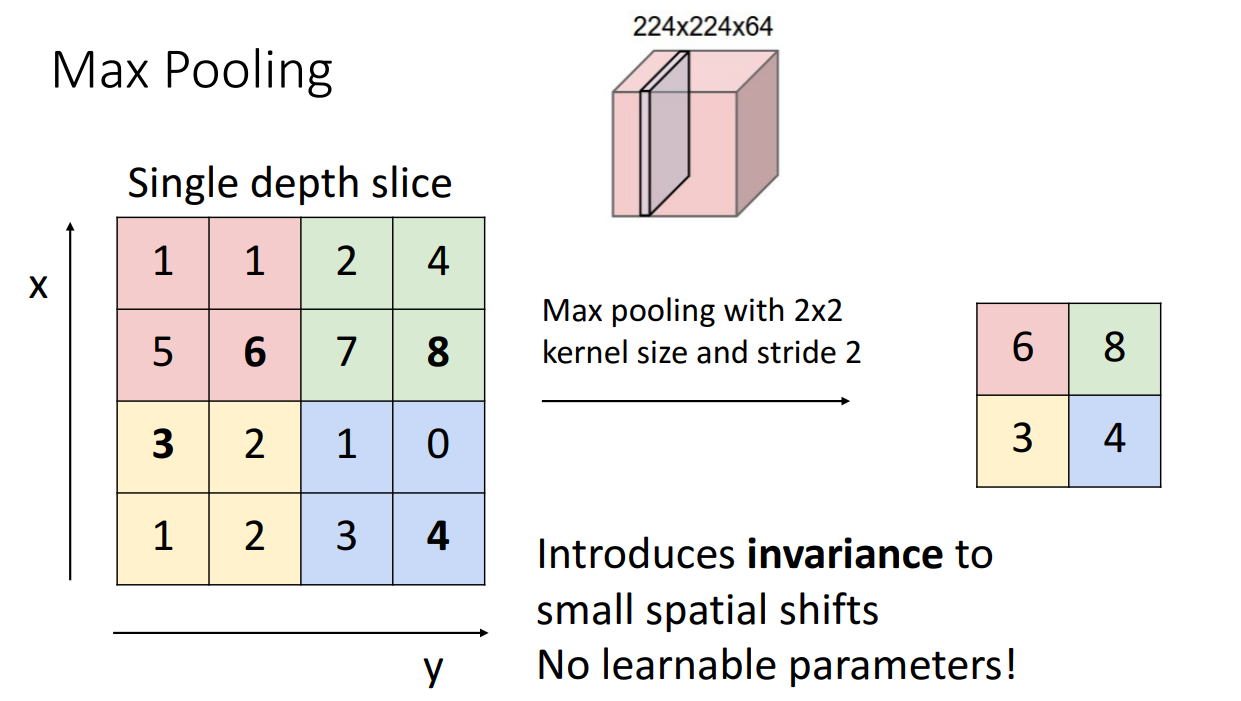
Kernel size, stride는 Convolutional Layer에서도 살펴봐서 괜찮고 Pooling function만 살펴보면 되겠습니다.
여러 함수들이 있겠지만 강의에 소개된 함수는 Max Pooling 입니다.
Max Pooling은 kernel size 크기에 맞춰서 해당 크기 안에 가장 큰 값만을 다음 층으로 보내는 함수입니다.
Max Pooling 외에도 평균 값을 다음 층으로 보내는 Average Pooling도 자주 사용합니다.

Pooling Layer 정리입니다.
Output의 크기를 구하는 식은 앞서 본 Conv Layer보다 훨씬 간단합니다.
왜냐하면 학습해야할 파라미터가 없기도 하고 설정해야할 하이퍼파라미터도 적기 때문입니다.
LeNet-5
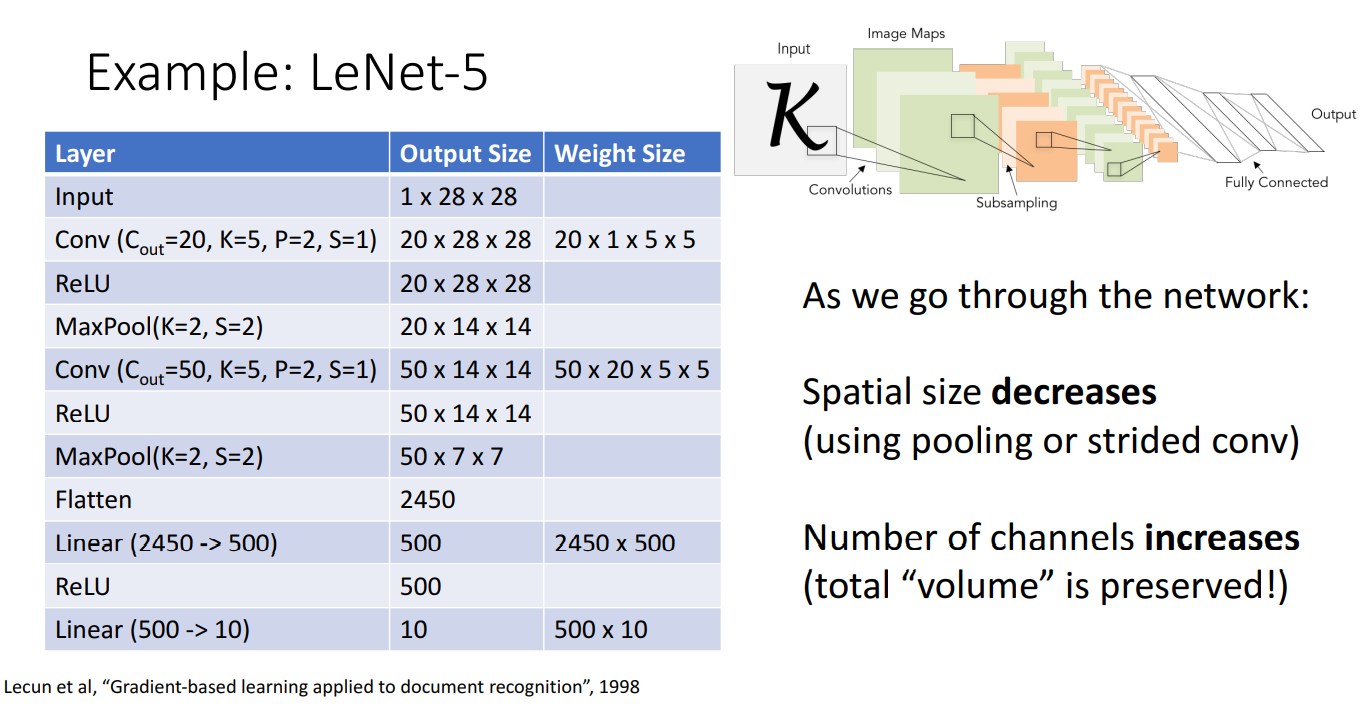
무려 1998년에 제안된 CNN 구조인 LeNet-5 입니다.
모델 구조를 보시면 Conv Layer - ReLU - Pooling Layer 순으로 여러겹 쌓여있고 마지막은 Linear Classifier를 통해서 클래스를 분류해주는 모습입니다.
Input 이미지를 보시면 Channel이 1 즉 Grayscale 이미지 분류를 위해 제시된 초기모델임을 알 수 있습니다.
초기 모델인 LeNet-5에서 CNN 구조의 문제점이 드러납니다.
먼저 Pooling Layer와 Strided Conv layer 를 거치면서 Spatial Size가 너무 작아지게 됩니다.
그리고 처음에 Grayscale이었던 Channel이 엄청나게 늘어나게됩니다.
이렇게 될 경우 네트워크가 학습되기 어렵습니다.
Batch Normalization

따라서 마지막 Convolutional 구조의 구성요소인 Normalization 개념이 나옵니다.
아이디어는 위에서 나와있듯 layer의 output을 평균이 0, 분산이 1이 되도록 정규화해주자는 겁니다.
효과는 internal covariate shift를 줄여서 최적화가 잘되도록 한다는 점입니다.
또한 주목할 점은 정규화 시키는 위 함수는 미분가능한 함수입니다.
따라서 네트워크 학습시 역전파시켜서 연산할 수 있습니다.
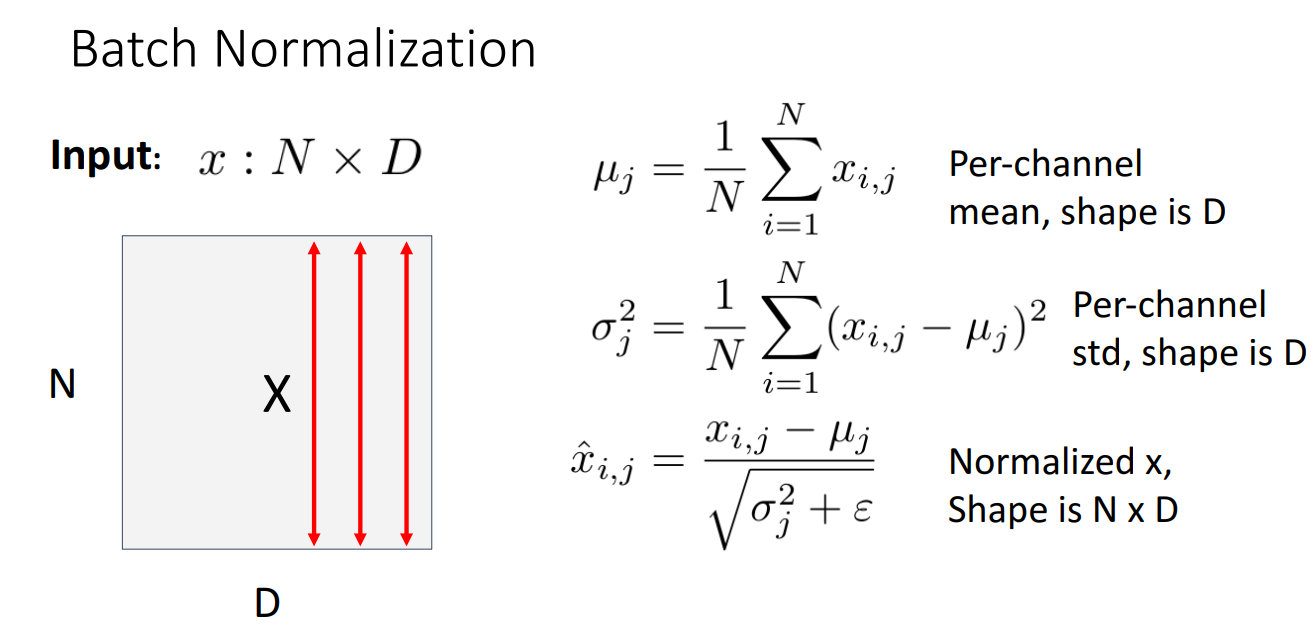
정규화 방법 중 가장 많이 쓰이고 성능 향상에도 좋은 방법이 Batch Normalization 입니다.
위 그림에서 빨간색 화살표 방향으로 알 수 있듯, 배치별로 정규화를 시키기 때문에 채널별로 정규화를 시키는 것과는 다른 개념입니다.
해당 방법에도 몇가지 문제점이 존재합니다.

첫번째는 평균을 0, 분산을 1로 정규화하는 과정이 어렵다는 것입니다.
이를 극복하기 위해 위와 같이 Learnable scale, shift parameters를 도입해서 이를 학습하도록 합니다.

두번째는 미니배치별로 정규화를 수행하기 때문에 Train 과정에서나 학습되지 Test 과정에서는 미니배치별로 예측을 수행하지 않기 때문에 사용할 수 없습니다.
이 경우에는 학습하는 대신 Fixed Scalar 값을 사용한다고 합니다.

따라서 CNN 에서 배치정규화가 사용되는 모습을 보시면 Channel을 건들지 않고 배치별로 하나씩 정규화 되는 것을 확인할 수 있습니다.
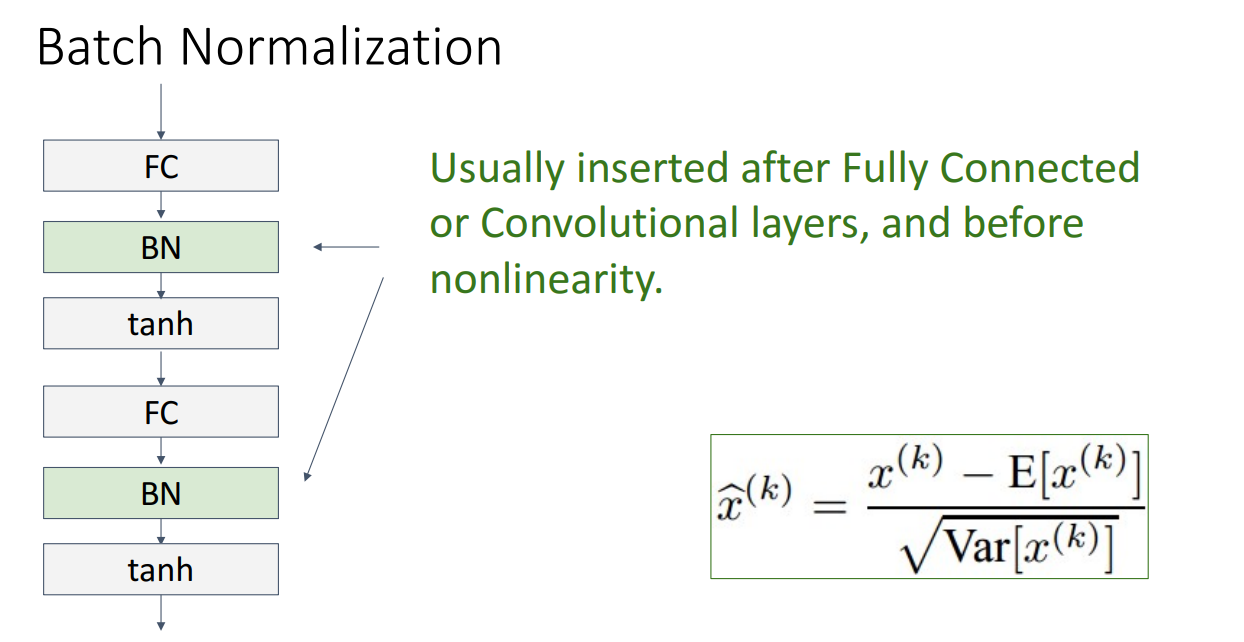
일반적으로 배치정규화는 FC layer나 Conv layer 뒤에, 활성화 함수 앞에 넣습니다.
이렇게함으로써 장점은 학습시키기 쉬워지고, 높은 학습률도 커버 가능하며, 더 빠르게 수렴한다는 점입니다.
하지만 단점은 아직 이론적으로 완벽하게 왜 좋은지 증명이 안되었으며, 학습과 추론시에 다르게 작동하기 때문에 버그가 자주 일어난다는 점입니다.
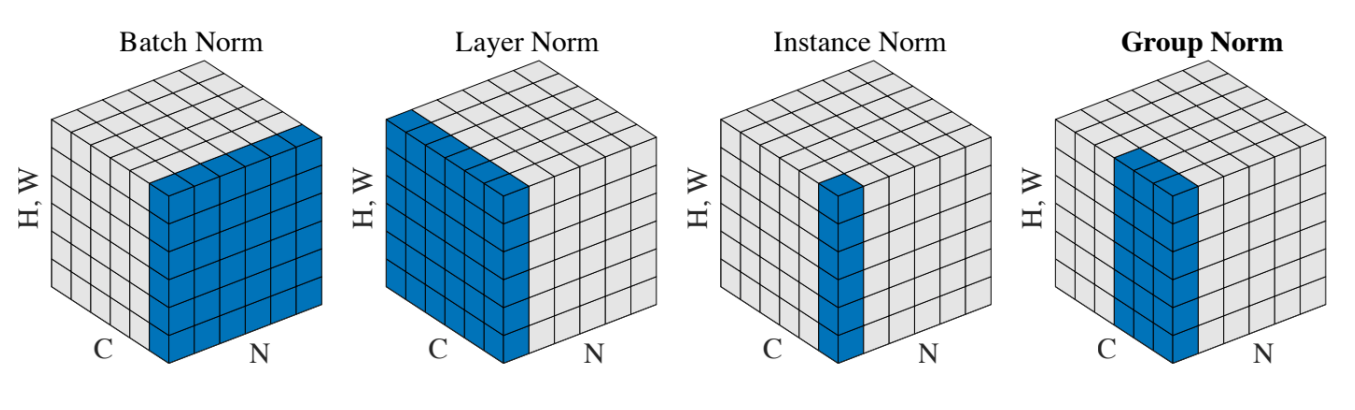
배치 정규화 이외에도 여러 정규화 방법들이 있는데 위 그림과 같이 정규화를 수행한다고 이해해주시면 되겠습니다.
